
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двухслойная модель турбулентного потокаСодержание книги Поиск на нашем сайте
Основной особенностью турбулентного режима движения является интенсивное перемешивание частиц жидкости. Поток жидкости в прямолинейной цилиндрической трубе круглого сечения. Процессы турбулентного перемешивания происходят по-разному. На твердой стенке (внутренняя поверхность трубы) скорости, и пульсационные, равны нулю. Вблизи твердой стенки находится тонкий слой, толщина его d в. В этом слое преимущественное влияние имеют касательные напряжения, рассчитываемые по закону вязкого трения Ньютона. Рассматриваемый слой назван вязким подслоем потока. В пределах вязкого подслоя скорость линейно увеличивается от нуля на стенке до некоторого значения ив на границе слоя. Пульсации скорости, давления и касательного напряжения передаются и в вязкий подслой.Интенсивность пульсаций продольной скорости в нем может достигать 0,3. Остальная часть поперечного сечения трубы занята турбулентным ядром потока, где и происходят интенсивные пульсации скорости и перемешивание частиц.
Полуэмпирическая теория турбулентности Л. Прандля Она основана на представлении о том, что при турбулентном перемешивании количество движения массы, переносимой в потоке за счет поперечной пульсационной составляющей скорости, остается неизменным на некотором пути, а затем изменяется скачком. Длина этого пути – так называемая длина пути перемешивания l. Предполагается, что это расстояние проходит моль жидкости, не взаимодействуя с другими молями и сохраняя постоянным свое осредненное количество движения. После прохождения этого пути моль жидкости смешивается с жидкостью другого слоя, отдавая ей разницу количества движения. Длина пути перемешивания имеет аналог в виде длины свободного пробега молекулы в молекулярно-кинетической теории. Но при этом средняя длина пробега молекул мала по сравнению с размерами поперечного сечения, а размеры турбулентных: вихрей (образований) могут быть сопоставимы с размерами сечения. Длина перемешивания – геометрическая величина, которая характеризует внутреннюю структуру потока при турбулентном движении, ее рассматривают как 1 из масштабов турбулентности.
Классификация потерь напора Потери удельной энергии, затрачиваемой на преодоление сопротивлений движению вязкой жидкости двух видов:1) потерь напора на преодоление гидравлических сопротивлений по длине, пропорциональных длине участков трубы, по которым движется жидкость, – потерь по длине hдл; 2) потерь напора на преодоление гидравлических сопротивлений в пределах коротких участков в непосредственной близости к тем или иным местным конструктивным устройствам труб – местных потерь напора hм. Общие потери напора в системе труб равны сумме потерь напора по длине отдельных участков и всех местных потерь напора: 3) неравномерное плавно изменяющееся движение: ламинарное и турбулентное; 4) неравномерное движение с изменением средней скорости и эпюры скоростей в пределах коротких участков, называемых местными сопротивлениями: ламинарное и турбулентное. Различие кинематической структуры для каждого из перечисленных видов движения определяет различие в расчетных зависимостях для потерь напора по длине.
29. Касательные напряжения и их распределение при равномерном движении. Рассмотрим равномерное напорное движение жидкости в прямолинейной наклонной трубе, рис. 7.5, радиусом r 0 с площадью живого сечения w и смоченным периметром c. Выделим отсек длиной l и составим уравнение равномерного движения массы жидкости, заключенной в отсеке. При равномерном движении сумма проекций на направление движения (на ось трубы) внешних сил, действующих на жидкость в выделенном отсеке, должна быть равна нулю:
где Р – равнодействующая сила давления в сечениях 1 - 1 и 2-2; Т – направленная против течения равнодействующая сил трения, действующих на боковой поверхность отсека c l; G – вес жидкости в выделенном отсеке. Тогда:
где t0 – касательное напряжение на стенке трубы; р 1 и р 2 – давления, действующие в центрах тяжести торцевых сечений отсека w1 = w2 = w; z 1 и z 2 – координаты центров тяжести этих сечений. Учитывая, что
Разделив все члены уравнения на rgw, получим:
При равномерном движении:
Тогда касательные напряжения на стенке трубы:
Так как w / c = R – гидравлический радиус, а hдл / l = J – гидравлический уклон, то:
или
Распределение касательных напряжений по сечению трубы может быть выяснено следующим образом. Выделим в потоке цилиндрический отсек жидкости, боковая поверхность которого отстоит от оси трубы на размер r, меньший чем радиус трубы r 0. Тогда для трубы получим:
где t – касательное напряжение, действующее на боковой поверхности выделенного в жидкости цилиндра с радиусом поперечного сечения r. Сравнивая (7.3) и (7.4), видим, что:
Так как r = r 0 – z', где z ' – расстояние по нормали от стенки трубы до рассматриваемой боковой поверхности отсека, то имеем:
Следовательно, при равномерном движении касательное напряжение по радиусу трубы распределено по линейному закону. Согласно (7.5) касательное напряжение на стенке (при z ' = 0) имеет максимальное значение, равное t0. На оси трубы касательное напряжение равно нулю. Приведем другую формулу для hдл:
Таким образом, видно что при равномерном движении потери напора по длине в данных условиях (l, r, g, R) можно определять через касательное напряжение на стенке.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 746; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.54.100 (0.009 с.) |

 . Количество движения массы равно:
. Количество движения массы равно:  . D Ттурб:
. D Ттурб:  или
или  . наз. силой турбулентного трения. Модуль касательного напряжения:
. наз. силой турбулентного трения. Модуль касательного напряжения:  . Общее касательное напряжение при турбулентном режиме движения равно сумме чисто вязкостного напряжения t лам и t турб. Тогда:
. Общее касательное напряжение при турбулентном режиме движения равно сумме чисто вязкостного напряжения t лам и t турб. Тогда: 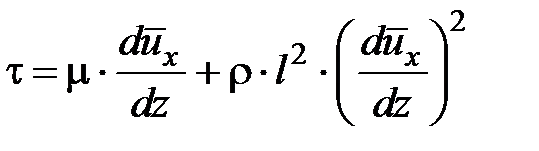 . При ламинарном движении нет перемешивания в жидкости:
. При ламинарном движении нет перемешивания в жидкости:  . Когда происходит интенсивное перемешивание в жидкости тогда:
. Когда происходит интенсивное перемешивание в жидкости тогда:  .
. . Эти потери энергии обусловлены переходом механической энергии потока в тепловую. Процесс этот необратим. Наличие гидравлических сопротивлений при движении вязкой жидкости связано с работой сил трения внутри жидкости. Благодаря силам трения механическая энергия может перейти в теплоту. Классификация движений по характеру поля скоростей (установившиеся движение): 1) равномерное движение с постоянными по длине средней скоростью и эпюрой скоростей: ламинарное и турбулентное; 2) неравномерное движение с постоянной по длине средней скоростью и изменяющейся по длине эпюрой скоростей: ламинарное и турбулентное;
. Эти потери энергии обусловлены переходом механической энергии потока в тепловую. Процесс этот необратим. Наличие гидравлических сопротивлений при движении вязкой жидкости связано с работой сил трения внутри жидкости. Благодаря силам трения механическая энергия может перейти в теплоту. Классификация движений по характеру поля скоростей (установившиеся движение): 1) равномерное движение с постоянными по длине средней скоростью и эпюрой скоростей: ламинарное и турбулентное; 2) неравномерное движение с постоянной по длине средней скоростью и изменяющейся по длине эпюрой скоростей: ламинарное и турбулентное; ,
, ,
, , имеем:
, имеем: .
. .
. .
. .
. ,
, . (7.3)
. (7.3) , (7.4)
, (7.4) .
. . (7.5)
. (7.5) .
.


