
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения равновесия жидкостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте (уравнения Л. Эйлера) Дифференциальные уравнения описывают зависимость массовых и поверхностных сил от координат какой-либо точки покоящейся жидкости. Для ввода этих уравнений выделим в покоящейся жидкости элементарный параллелепипед со сторонами На грани параллелепипеда со стороны окружающей жидкости действуют поверхностные силы – силы гидростатического давления Установим связь между гидростатическим давление в точке А ( Силы гидростатического давления на грани параллелепипеда
Рис. 3. К выводу уравнения Л. Эйлера
Эти же силы гидростатического давления, выраженные через гидростатическое давление в т. А.
Здесь Равнодействующая массовых сил
Условие равновесия выделенного параллелепипеда:
Рассмотрим случай
или в развернутом виде:
где
После простейшего преобразования получаем
Таким образом, условием равновесия жидкости будет
В таком виде система уравнений была получена Л. Эйлером в 1775 году. Система дифференциальных уравнений показывает, что градиенты гидростатического давления в направлении каждой из координат осей равны проекциям на эти же оси единичных массовых сил.
Уравнение гидростатики Умножим каждый из членов, входящих в систему (13) дифференциальных уравнений, соответственно на
Уравнение (14) является аналитическим выражением распределения гидростатического давления жидкости. Для случая покоящейся жидкости гидростатическое давление Таким образом, приведенное выше уравнение (14) приобретает следующий вид:
Применим уравнение (15) к случаю абсолютного покоя жидкости, когда массовой силой является только сила тяжести. При принятом направлении координатных осей проекции этой силы будут:
а уравнение (15) применительно к точке получает вид:
После интегрирования получим:
При
Уравнение (16) называется основным уравнением гидростатики.
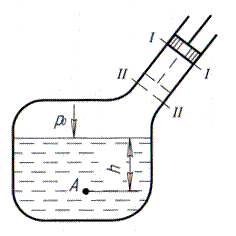
Закон Паскаля «Если жидкость находится в состоянии покоя, то изменение давления на любой внешней поверхности, возникающее от действия внешних сил, передается без изменения во все точки объема, занимаемого данной жидкостью». Доказательство из уравнения (16). Абсолютное давление в т. А при размещении поршня в положении –
После перемещения поршня в положение
т.е. при изменении давления на свободной поверхности на
Рис. 3а. Схема действия давления по закону Паскаля.
Эта идея использована Паскалем в принципиальной концепции гидропроцесса.
Пьезометрическая высота Слово «пьезометрическая» от греческого означает «давление»+«мера». В закрытом сосуде с жидкостью установим две трубки на уровне ВА, причем у одной из них запаян конец и отсутствует давление ( Внутри сосуда зададим давление
Рис. 4. Пьезометрическая высота.
Вакуум – разность между атмосферным и абсолютным давлением - «пустота» (лат.) или недостаток давления (рис. 5)
Рис. 5. Схема измерения вакуума
Напор Рассмотрим точку К (рис. 6) на произвольной глубине h по отношению к плоскости сравнения 0 – 0. В точке К установим пьезометр. Пьезометрический напор
где Аналогично определим напор в точке С:
Очевидно, что Отсюда следует, что напор
Далее опустим в сосуд на малую глубину трубку Е, предварительно выкачав из нее воздух. По этой трубке жидкость поднимается на высоту
Рис 6. Схема расчета напора
Таким образом, при учете гидростатического напора учитывают атмосферное давление
|
||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 723; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

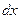 ,
, 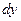 ,
,  и с центром в точке А, ориентируем этот параллелепипед относительно координатных осей
и с центром в точке А, ориентируем этот параллелепипед относительно координатных осей 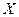 ;
; 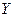 ;
; 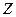 (рис. 3).
(рис. 3).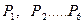 направленные внутрь параллелепипеда и массовые силы – сила тяжести и сила инерции переносного движения. Равнодействующая массовых сил
направленные внутрь параллелепипеда и массовые силы – сила тяжести и сила инерции переносного движения. Равнодействующая массовых сил 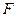 .
. ) и массовыми силами.
) и массовыми силами.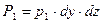 ;
;  ;
;  ;
;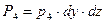 ;
; 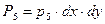 ;
;  .
.
 ;
; 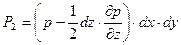 и т.д.
и т.д.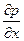 ;
; 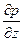 и т.д. градиенты давления по соответствующим координатным осям.
и т.д. градиенты давления по соответствующим координатным осям. .
. ;
;  ;
; 
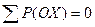 .
. ,
,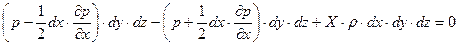
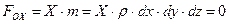 ;
;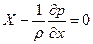 , а по аналогии для других координатных осей
, а по аналогии для других координатных осей 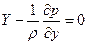 ;
;  .
.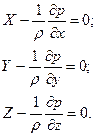 (13)
(13)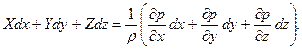 (14)
(14) . Следовательно, правая часть уравнения (14) представляет полный дифференциал давления
. Следовательно, правая часть уравнения (14) представляет полный дифференциал давления 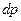 .
.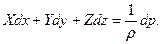 (15)
(15)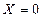 ;
; 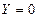 ;
; 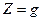 ,
,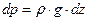 .
.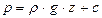
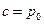 – давление на свободной поверхности, а
– давление на свободной поверхности, а 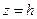 – глубина погружения в жидкости точки, для которой определяется давление:
– глубина погружения в жидкости точки, для которой определяется давление: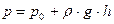 (16)
(16)
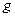
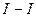 (рис.3):
(рис.3):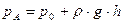 (17)
(17)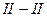 (рис. 3а) давление на свободной поверхности увеличится на величину
(рис. 3а) давление на свободной поверхности увеличится на величину  и будет равно
и будет равно 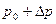 , а абсолютное давление в т. А будет равно
, а абсолютное давление в т. А будет равно ,
,
 ), а другая имеет открытый конец (
), а другая имеет открытый конец (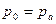 ) (рис. 4).
) (рис. 4). 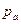 называется атмосферным давлением окружающего нас воздуха. Это давление изменяется во времени и с изменением высоты местности. За нормальное атмосферное давление принимается
называется атмосферным давлением окружающего нас воздуха. Это давление изменяется во времени и с изменением высоты местности. За нормальное атмосферное давление принимается  , что соответствует
, что соответствует 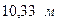 столба пресной воды и
столба пресной воды и 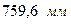 столба ртути. При решении задач за атмосферное давление принимают
столба ртути. При решении задач за атмосферное давление принимают  .
. . Жидкость в правой трубке поднимается на высоту
. Жидкость в правой трубке поднимается на высоту 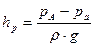 , получившей название избыточной пьезометрической высоты; в левой трубке жидкость поднимается на уровень
, получившей название избыточной пьезометрической высоты; в левой трубке жидкость поднимается на уровень 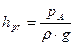 , получившей название абсолютной пьезометрической высоты, а
, получившей название абсолютной пьезометрической высоты, а 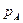 называется абсолютным давление в точке А.
называется абсолютным давление в точке А.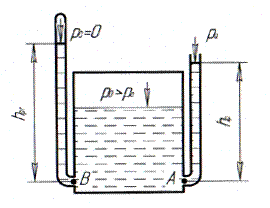
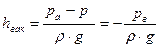 (18)
(18)
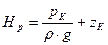
 – геометрический напор.
– геометрический напор.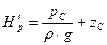
 .
. состоит из удельной потенциальной энергии давления
состоит из удельной потенциальной энергии давления  и удельной потенциальной энергии положения
и удельной потенциальной энергии положения  (геометрический напор).
(геометрический напор).
 равную приведенной пьезометрической высоте. Сумма двух линейных величин
равную приведенной пьезометрической высоте. Сумма двух линейных величин 
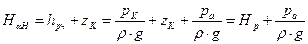 (19)
(19) .
.


