
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение постоянства расходаСодержание книги Поиск на нашем сайте
Уравнение постоянства расхода
Основные теоретические сведения
Объёмным расходом потока Q называется объём жидкости V, проходящий в единицу времени t через живое сечение потока, м3/с:
Q =
Массовым расходом потока Qm называется масса жидкости m, проходящий в единицу времени t через живое сечение потока, кг/с:
Qm =
Уравнение неразрывности течения (сплошности потока) в интегральной форме в случае одномерного приближения принимает вид уравнения постоянства расхода: · для слобосжимаемой (или трудносжимаемой) жидкости (r = const) это уравнение постоянства объёмного расхода – объёмный расход потока вдоль по течению неизменен.
Q = v × w, (6.3)
где Q – объёмный расход, м3/с; v – средняя скорость в живом (поперечном) сечении потока, м/с; w – площадь живого (поперечного) сечения потока, м2. · для сжимаемой жидкости (r ¹ const) это уравнение постоянства массового расхода – массовый расход потока вдоль по течению неизменен.
Qm = r × v × w, (6.4)
где Qm – массовый расход, кг/с r – плотность жидкости, кг/м3.
Примеры решения задач
Пример № 6.1. Определите массу жидкости плотностью 780 кг/м3, которая пройдёт через живое сечение круглого напорного трубопровода диаметром d = 0,2 м за 10 минут. Средняя скорость жидкости в поперечном сечении потока v равна 1,5 м/с.
Решение
Массу жидкости, проходящую через живое сечение трубопровода за время t можно определить из уравнения (6.2) Qm =
m = Qm × t.
В системе СИ время t = 10 × 60 = 600 с. Массовый расход жидкости определяем, используя уравнение постоянства массового расхода (6.4). Учитываем, что для круглого напорного трубопровода площадь живого сечения w =
Qm = r × v × w = r × v ×
Qm = 780 × 1,5 ×
Искомая масса жидкости равна:
m = 36,738 × 600 = 22042,8 (кг).
Пример № 6.2. Определите размер квадратного напорного трубопровода. За 3 минуты через поперечное сечение трубопровода проходит 7,2 м3 жидкости постоянной плотности. Средняя скорость потока в живом сечении составляет 1,0 м/с.
Решение
Размер, то есть сторону квадратного напорного трубопровода при r = const можно определить из уравнения постоянства объёмного расхода (6.3) Q = v × w:
w =
Для квадратного напорного трубопровода площадь живого (поперечного) сечения потока w = a2. Тогда размер трубопровода равен:
а =
По уравнению (6.1) объёмный расход потока Q равен:
Q =
В системе СИ время t = 3 × 60 = 180 с.
Q =
w =
а =
Уравнение Бернулли для потока идеальной жидкости (без учёта потерь энергии)
Примеры решения задач
Пример № 7.1.
Дано: d1 = 0,02 м; d2 = 0,12 м; D h = 250 мм = 0,25 м.
Рисунок 7.1 Определить: Q.
Решение
Составим уравнение Бернулли (энергии) без учёта потерь энергии для двух сечений: 1-1 и 2-2:
z1 +
Для горизонтального трубопровода z1 = z2. Обозначим пьезометрические высоты h1 =
D h = a2 ×
Из уравнения неразрывности v 1 × w1 = v 2 × w2 выразим скорость во втором сечении:
v 2 = v 1 ×
Для круглого напорного трубопровода площадь живого сечения потока w =
v 2 = v 1 ×
Подставляя это выражение в уравнение Бернулли имеем:
D h = a2 ×
Считаем, что течение жидкости в трубопроводе турбулентное. Принимаем коэффициент Кориолиса a1 = a2 = a = 1,1.
D h = a ×
v 1 =
Объёмный расход равен:
Q = v 1 × w1 = v 1 ×
Пример № 7.2. Жидкость вытекает из резервуара большого сечения по горизонтальному трубопроводу переменного сечения. Определить расход Q в горизонтальном трубопроводе (рис. 7.2), скорость на каждом из участков vi и построить пьезометрическую линию
Дано: Н = 5 м; d1 = 15 мм = 0,015 м; d2 = 20 мм = 0,020 м; d3 = 10 мм = 0,010 м. Определить: Q, v1, v2, и v3.
Рисунок 7.2 Решение
Составим уравнение Бернулли (энергии) без учёта потерь энергии для двух сечений: 0-0 (свободная поверхность жидкость в резервуаре, из которого истекает жидкость) и 3-3 (выходное сечение трубопровода):
z0 +
Здесь р0 – давление на свободную поверхность жидкости в открытом резервуаре равно атмосферному давлению, то есть р0 = рбар. р3 – давление в выходном сечении трубопровода. Оно равно давлению той среды, куда происходит истечение. В данном случае р3 = рбар. Горизонтальную плоскость сравнения совместим с осью трубопровода переменного сечения. Тогда z0 = Н, а z3 = 0. Скорость на свободной поверхности жидкости в резервуаре v0 пренебрежимо мала по сравнению со скоростью жидкости в трубопроводе переменного сечения vi. Поэтому полагаем, что v0» 0. Принимаем, что коэффициент Кориолиса a. 3 =1,0. (На практике мы обычно имеем дело с турбулентным движением жидкости.). Уравнение Бернулли имеет вид:
Н + или Н = Отсюда v3 =
Используя уравнение неразрывности течения определяем расход жидкости в трубопроводе:
Q = v3 × w3 = v ×
Используя это же уравнение, определяем скорости на участках диаметром d1 и d2:
Q = v1 × w1. Þ v1 =
Q = v2 × w2. Þ v2 =
Пьезометрическую линию строят, исходя из следующих положений. Поскольку задача решается без учёта потерь энергии, то напорная линия (линия полной энергии) -
Рисунок 7.3 – Построение пьезометрической линии
Примеры решения задач
Пример № 8.1. При каком режиме будет протекать вода с температурой Дано Q = 0,56 м3/с; h = 0,7 м; b = 0,8 м.
Решение
При температуре Для определения режима течения необходимо сравнить расчётное число Рейнольдса Re с критическим значением. Принимаем, что критическое значение числа Рейнольдса равно Reкр = 2320. Расчётное число Рейнольдса определяем по формуле:
Red экв =
где v -средняя скорость течения воды в открытом лотке;
n - кинематический коэффициент вязкости м2/с. Среднюю скорость течения воды в открытом лотке определяем из уравнения неразрывности течения
Q = v × w,
где w – площадь живого (поперечного) сечения потока, м2. Для прямоугольного лотка площадь живого сечения равна
w = h × b. Тогда v =
Диаметр эквивалентный dэкв – это отношение четырёх площадей живого сечения потока w к смоченному периметру c:
dэкв =
Смоченный периметр c (хи) – часть периметра живого сечения, на которой жидкость соприкасается с твёрдыми стенками. Для открытого прямоугольного лотка смоченный периметр равен c = h + h + h = 2 × h + b.
dэкв =
Red экв =
Re > Reкр, следовательно режим движения турбулентный.
Пример № 8.2. По напорному трубопроводу переменного сечения подаётся жидкость с объёмным расходом Q = 0,6 л/с. Кинематический коэффициент вязкости жидкости 3,2×10-6 м2/с. Определите диаметр, при котором произойдёт смена режима движения.
Дано Q = 0,6 л/с = 0,6×10-3 м3/с; n = 3,2×10-6 м2/с.
Решение
Смена режима движения происходит при Reкр =
Reкр =
где v -средняя скорость в поперечном сечении потока; d - диаметр трубопровода, м; n - кинематический коэффициент вязкости м2/с. Среднюю скорость течения жидкости выразим из уравнения неразрывности течения Q = v × w:
v =
где w – площадь живого (поперечного) сечения потока, м2. Для круглого напорного трубопровода площадь живого сечения потока равна:
w = Тогда v =
Подставляем это выражение в формулу для определения числа Рейнольдса:
Reкр =
Отсюда диаметр, при котором происходит смена режима течения, равен:
d =
Принимаем, что критическое значение числа Рейнольдса равно Reкр = 2320. Тогда
d =
Примеры решения задач
Пример № 10.1. Определить потери давления на трение D ртр в стальной трубе квадратного сечения. Длина трубы l = 80 м, площадь живого сечения w = 2,25×10-2 м2, средняя скорость движения воды v = 5 м/с, температура воды 20 0С.
Справочные данные
- плотность воды r = 998,2 кг/м3; - абсолютная эквивалентная шероховатость kэ = 0,05 мм; - кинематический коэффициент вязкости n = 1,01´10-6 м2/с.
Решение
Потери давления на трение определяем по формуле Дарси-Вейсбаха:
D ртр = l ×
где dэкв – эквивалентный диаметр рассматриваемого участка трубы, м;
r - плотность жидкости, кг/м3; v – средняя скорость течения жидкости в сечении потока, м/с. Диаметр эквивалентный dэк в равен отношение четырёх площадей живого сечения потока w к смоченному периметру c. Для трубопровода квадратного сечения со стороной а диаметр эквивалентный равен:
dэкв =
Величину а определяем из площади квадрата (w = а2). а = Определяем режим течения жидкости в трубопроводе:
Re =
Значение числа Рейнольдса больше критического (Reкр = 2320), следовательно, режим течения жидкости турбулентный. Определяем значение критерия зоны турбулентности:
Re ×
Значение критерия зоны сопротивления находится в пределах от 10 до 500, следовательно движение происходит в области смешанного сопротивления, для которой справедлива формула Альтшуля:
l = 0,11 ×
Потери давления на трение равны:
D ртр = 0,0158 ×
Пример № 10.2. Определить потери напора и гидравлический уклон при подаче воды со скоростью v = 0,2 м/с через умеренно заржавленную стальную трубку диаметром d = 50 мм и длиной l = 60 м при температуре воды 10 0С.
Справочные данные
- кинематический коэффициент вязкости n = 1,31´10-6 м2/с; - абсолютная эквивалентная шероховатость kэ = 0,45 мм.
Решение
Потери напора на трение определяем по формуле Дарси-Вейсбаха:
D hтр = l ×
где
v – средняя скорость течения жидкости в сечении потока, м/с. Определяем режим течения жидкости в трубопроводе:
Re =
Значение числа Рейнольдса больше критического (Reкр = 2320), следовательно, режим течения жидкости турбулентный. Определяем значение критерия зоны турбулентности:
Re ×
Значение критерия зоны сопротивления меньше 10, следовательно движение происходит в области «гидравлически гладких» труб, для которой справедлива формула Блазиуса:
l =
D hтр = 0,0338 ×
Гидравлическим уклоном i называется отношение потерь напора D hтр к длине участка l, на котором эти потери происходят:
i =
Примеры решения задач
Пример № 11.1. В качестве нагревательных приборов системы отопления использованы стальные трубы d1 = 0,6 м. Стояк, подводящий нагретую воду, и соединительные линии выполнены из труб диаметром d2 = 0,025 м и приварены к торцам нагревательных труб (рис. 9.1). Определить суммарные потери давления на участке между сечениями А-А и В-В, если скорость движения горячей воды в подводящих линиях v2 = 1,0 м/с. Радиус поворота нагревательной трубы Rп = 0,6 м, а длина нагревательной трубы l1 = 4,0 м. Температура воды
l1 = 4,0 м; Rп = 0,6 м; d2 = 0,025 м; v2 = 1,0 м/с;
Справочные данные: r = 965,3 кг/м3; n = 0,33×10-6 м2/с; kэ = 6,5×10-4 м; при плавном повороте трубопровода круглого сечения на 1800 а = 1,33. Определить: рпот.
Решение
Общие потери давления в системе между сечениями А-А и В-В русел равны арифметической сумме потерь давления по длине l1 и всех потерь, вызванных отдельными местными сопротивлениями (внезапное расширение, плавный поворот на 1800 и внезапное сужение).
рпот =
Потери давления на трение по длине на участке длиной l1 определяем по формуле Дарси-Вейсбаха, Па:
D ртр = l1 ×
где
r - плотность жидкости, кг/м3; v 1 – средняя скорость течения жидкости в сечении потока, м/с. Используя уравнение неразрывности течения определяем скорость на участке диаметром d1, м/с:
Q = v1 × w1 = v2 × w2.
Отсюда
v1 =
Определяем режим течения жидкости на участке трубопровода диаметром d1 и длиной
Re1 =
Re > Reкр = 2000…2320, следовательно режим движения турбулентный. Для определения области сопротивления рассчитываем значение критерия зоны турбулентности:
Re ×
Значение критерия зоны турбулентности меньше 10, следовательно движение происходит в области «гидравлически гладких» труб, для которой справедлива формула Блазиуса:
l1 =
Потери давления на трение по длине
D ртр = 0,0424 ×
Потери давления на местных сопротивлениях определяем по формуле Вейсбаха, Па:
D рм = z × r ×
где z – коэффициент местного сопротивления, безразмерный. При резких переходах в местных сопротивлениях коэффициент z не зависит от значения числа Рейнольдса при Re ³ 3000. Следовательно, при определении коэффициентов местного сопротивления мы можем использовать формулы для автомодельной области (3), (4), (10) – (16); r – плотность жидкости, кг/м3; v – средняя скорость в сечении, обычно после местного сопротивления, м/с. Однако при определении потерь энергии при расширении трубопровода расчёт принято проводить для скорости до местного сопротивления. В данном случае до местного сопротивления (внезапного расширения) диаметр d2 и скорость v2. Потери давления и коэффициент местного сопротивления, отнесённый к средней скорости до местного сопротивления, определяем по формулам (2) и (3), которые в данном случае записываются в виде:
D рм в.р. = zв.р. × r ×
zв.р. =
где w2 - площадь трубопровода до расширения; w1 - площадь трубопровода после расширения.
zв.р. =
Потери давления при внезапном расширении трубопровода равны, Па:
D рм в.р. = 0,997 × 965,3 ×
II вариант (по потерянной скорости)
Если принять коэффициент Кориолиса a = 1, то потери давления можно определить по формуле Борда (5, б), Па:
D рв.р. = r ×
где
D рв.р. = 965,3 ×
Потери давления при плавном повороте трубопровода на 1800 определяем по формуле:
D рм 180 = z180 × r ×
Коэффициент сопротивления при плавном повороте трубопровода на Q = 1800 определяем по формуле (15):
z180. = а × z90,
где а – справочный коэффициент, зависящий от угла поворота. При повороте на 1800 а = 1,33; z90 – коэффициент местного сопротивления при плавном повороте трубы на 900. Коэффициент местного сопротивления при плавном повороте трубы на 900 определяем по эмпирической формуле Альтшуля (16):
z90 =
где d1 – диаметр нагревательной трубы, м; Rп – радиус закругления трубы, м.
z90 =
z180. = 1,33 × 104,654 = 139,190.
D рм 180 = 139,190×965,3 ×
Потери давления при внезапном сужении трубопровода равны:
D рм в.с. = zв.с. × r ×
Коэффициент местного сопротивления на внезапном сужении zв.с определяем по формуле (10):
zв.с. =
Коэффициент сжатия струи e зависит оцениваем по эмпирической формуле (12):
e = 0,57 +
Степень сжатия потока n равна:
n =
e = 0,57 +
zв.с. =
D рм в.с. = 0,412 × 965,3 ×
Общие потери давления в системе равны:
D рпот = 0,000394 + 481,202 + 0,194 + 198,852 = 680,2484 (Па).
Уравнение постоянства расхода
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 982; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.253.87 (0.009 с.) |

 . (6.1)
. (6.1)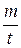 . (6.2)
. (6.2)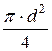 .
. = 36,738 (кг/с).
= 36,738 (кг/с). .
. .
.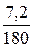 = 0,04 (м3/с).
= 0,04 (м3/с).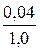 = 0,04 (м2).
= 0,04 (м2). = 0,2 (м).
= 0,2 (м). Определить расход жидкости Q в горизонтальном трубопроводе диаметром d1 = 0,2 м, имеющем сужение диаметром d2 = 0,12 м (рис. 7.1). Разность показаний пьезометров D h = 250 мм.
Определить расход жидкости Q в горизонтальном трубопроводе диаметром d1 = 0,2 м, имеющем сужение диаметром d2 = 0,12 м (рис. 7.1). Разность показаний пьезометров D h = 250 мм. + a1 ×
+ a1 ×  = z2 +
= z2 +  + a2 ×
+ a2 ×  .
. .
. .
. - a1 ×
- a1 ×  .
.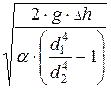 =
=  = 0,815 (м/с).
= 0,815 (м/с). = 0,815
= 0,815  = 0,0256 (м3/с).
= 0,0256 (м3/с). . Напор над центром отверстия, к которому присоединён трубопровод, Н равен 5 м. Диаметры различных участков трубопровода соответственно равны: d1 = 15 мм, d2 = 20 мм, d3 = 10 мм.
. Напор над центром отверстия, к которому присоединён трубопровод, Н равен 5 м. Диаметры различных участков трубопровода соответственно равны: d1 = 15 мм, d2 = 20 мм, d3 = 10 мм.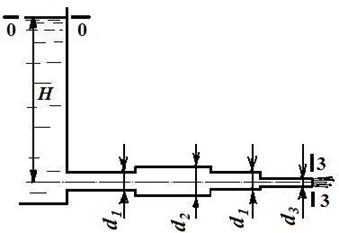
 + a0 ×
+ a0 ×  = z3 +
= z3 +  + a3 ×
+ a3 ×  .
. + 0 = 0 +
+ 0 = 0 + 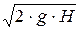 =
=  = 9,9 (м/с).
= 9,9 (м/с). = 9,9 ×
= 9,9 × 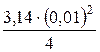 = 0,00078 (м3/с).
= 0,00078 (м3/с). =
=  =
=  = 4,42 (м/с);
= 4,42 (м/с);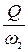 =
= 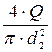 =
=  = 2,48 (м/с).
= 2,48 (м/с). будет представлять собой горизонтальную прямую, являющуюся продолжением свободной поверхности воды в сечении 0-0. Пьезометрическая линия
будет представлять собой горизонтальную прямую, являющуюся продолжением свободной поверхности воды в сечении 0-0. Пьезометрическая линия  расположиться ниже напорной линии на величину
расположиться ниже напорной линии на величину  в каждом сечении. Таким образом, отложив вниз от напорной линии величины
в каждом сечении. Таким образом, отложив вниз от напорной линии величины  =
=  = 0,987 (м);
= 0,987 (м);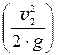 =
=  = 0,312 (м);
= 0,312 (м); =
=  = 5 (м).
= 5 (м).
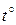 = 15 °С в открытом прямоугольном лотке, если объёмный расход жидкости Q равен 0,56 м3/с, глубина воды в лотке b = 0,7 м, а ширина лотка b = 0,8 м.
= 15 °С в открытом прямоугольном лотке, если объёмный расход жидкости Q равен 0,56 м3/с, глубина воды в лотке b = 0,7 м, а ширина лотка b = 0,8 м. ,
, - диаметр эквивалентный, м;
- диаметр эквивалентный, м; =
= 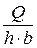 =
=  = 1,0 м/с.
= 1,0 м/с.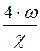
 =
=  =
=  = 1,02 м.
= 1,02 м. = 886956,52.
= 886956,52. для цилиндрических напорных труб:
для цилиндрических напорных труб: = 2000…2320,
= 2000…2320, .
. =
=  .
. .
. = 0,1 (м).
= 0,1 (м). × r ×
× r ×  ,
,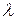 - коэффициент гидравлического трения (коэффициент Дарси), безразмерный;
- коэффициент гидравлического трения (коэффициент Дарси), безразмерный;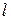 - длина трубопровода, м;
- длина трубопровода, м; - диаметр трубопровода, м;
- диаметр трубопровода, м;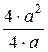 = а.
= а. =
=  = 0,15 м.
= 0,15 м. = 742574,26.
= 742574,26. = 742574,26 ×
= 742574,26 ×  = 247,86.
= 247,86. = 0,11 ×
= 0,11 ×  = 0,0158.
= 0,0158.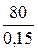 × 998,2 ×
× 998,2 ×  = 105143,73 Па.
= 105143,73 Па. ×
× 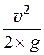 ;
; =
=  = 7633,59.
= 7633,59. = 9,16.
= 9,16. =
=  ×
×  = 0,083 м.
= 0,083 м. =
=  = 0,00138 м/м.
= 0,00138 м/м. = 90 0С.
= 90 0С. Дано: d1 = 0,6 м;
Дано: d1 = 0,6 м;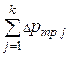 +
+  = D ртр 1 + D рм в.р +D рм 180 +D рм в.с..
= D ртр 1 + D рм в.р +D рм 180 +D рм в.с..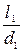 × r ×
× r ×  ,
, - длина трубопровода, м;
- длина трубопровода, м; - диаметр трубопровода, м;
- диаметр трубопровода, м; =
=  =
=  =
=  = 0,0017 м/с.
= 0,0017 м/с. :
: =
=  = 3090,909.
= 3090,909.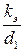 = 3090,909 ×
= 3090,909 ×  = 3,348.
= 3,348. =
=  = 0,0424.
= 0,0424. × 965,3 ×
× 965,3 ×  = 0,000394 (Па).
= 0,000394 (Па).
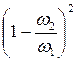 ;
; =
=  =
=  = 0,997.
= 0,997. = 481,202.
= 481,202. ,
, - скорость до местного сопротивления, м/с;
- скорость до местного сопротивления, м/с; - скорость после местного сопротивления, м/с;
- скорость после местного сопротивления, м/с; - потерянная скорость, м/с.
- потерянная скорость, м/с. = 481,01 (Па).
= 481,01 (Па). .
. ,
, = 104,654.
= 104,654. .
. .
. =
=  =
=  =
= 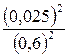 = 0,0017.
= 0,0017. = 0,609.
= 0,609. = 0,412.
= 0,412.


