
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ламинарный и турбулентный режимы движения жидкости. Число Рейнольдса и его критическое значениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные теоретические сведения
Различают ламинарный и турбулентный режимы движения жидкостей. Движение жидкости, при котором отсутствуют изменения (пульсации) местных скоростей, приводящие к перемешиванию жидкости, называют ламинарным (от латинского слова lamina – слой, пластинка). Движение жидкости, при котором происходят изменения (пульсации) местных скоростей, приводящие к перемешиванию жидкости называют турбулентным (от латинского слова turbulentus – беспорядочный, бурный). В общем случае режим движения жидкости определяется безразмерным комплексом, называемым числом (критерием) Рейнольдса
Re =
где v - средняя скорость течения, м/с; L - характерный поперечный размер потока, м; r - плотность жидкости, кг/м3; h - динамический коэффициент вязкости, Па × с; n - кинематический коэффициент вязкости, м2/с. Число Рейнольдса характеризует отношение сил инерции к силам трения (вязкости). Для круглых напорных труб в качестве характерного геометрического размера живого сечения потока принимают диаметр трубы d. Для некруглых и безнапорных труб в качестве характерного геометрического размера живого сечения потока труб принимают гидравлический радиус R или диаметр эквивалентный dэкв.:
dэкв =
R =
где w - живое сечение потока - поперечное сечение потока, перпендикулярное его направлению; c (хи) – смоченный периметр, часть периметра живого сечения, на которой жидкость соприкасается с твёрдыми стенками. Для напорных трубопроводов круглого сечения число Рейнольдса вычисляется по формуле:
Red =
Для всех иных поперечных сечений, а также для открытых русел и безнапорных потоков:
Red экв =
Если число Рейнольдса меньше критического (Re < Reкр) наблюдается ламинарное движение. При Re > Reкр будет турбулентное течение жидкости. В качестве критического числа Рейнольдса принят
Reкр =
где Применительно к формуле (8.6)
Примеры решения задач
Пример № 8.1. При каком режиме будет протекать вода с температурой Дано Q = 0,56 м3/с; h = 0,7 м; b = 0,8 м.
Решение
При температуре Для определения режима течения необходимо сравнить расчётное число Рейнольдса Re с критическим значением. Принимаем, что критическое значение числа Рейнольдса равно Reкр = 2320. Расчётное число Рейнольдса определяем по формуле:
Red экв =
где v -средняя скорость течения воды в открытом лотке;
n - кинематический коэффициент вязкости м2/с. Среднюю скорость течения воды в открытом лотке определяем из уравнения неразрывности течения
Q = v × w,
где w – площадь живого (поперечного) сечения потока, м2. Для прямоугольного лотка площадь живого сечения равна
w = h × b. Тогда v =
Диаметр эквивалентный dэкв – это отношение четырёх площадей живого сечения потока w к смоченному периметру c:
dэкв =
Смоченный периметр c (хи) – часть периметра живого сечения, на которой жидкость соприкасается с твёрдыми стенками. Для открытого прямоугольного лотка смоченный периметр равен c = h + h + h = 2 × h + b.
dэкв =
Red экв =
Re > Reкр, следовательно режим движения турбулентный.
Пример № 8.2. По напорному трубопроводу переменного сечения подаётся жидкость с объёмным расходом Q = 0,6 л/с. Кинематический коэффициент вязкости жидкости 3,2×10-6 м2/с. Определите диаметр, при котором произойдёт смена режима движения. Дано Q = 0,6 л/с = 0,6×10-3 м3/с; n = 3,2×10-6 м2/с.
Решение
Смена режима движения происходит при Reкр =
Reкр =
где v -средняя скорость в поперечном сечении потока; d - диаметр трубопровода, м; n - кинематический коэффициент вязкости м2/с. Среднюю скорость течения жидкости выразим из уравнения неразрывности течения Q = v × w:
v =
где w – площадь живого (поперечного) сечения потока, м2. Для круглого напорного трубопровода площадь живого сечения потока равна:
w = Тогда v =
Подставляем это выражение в формулу для определения числа Рейнольдса:
Reкр =
Отсюда диаметр, при котором происходит смена режима течения, равен:
d =
Принимаем, что критическое значение числа Рейнольдса равно Reкр = 2320. Тогда
d =
|
||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 2256; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.70.92 (0.008 с.) |

 =
=  , (8.1)
, (8.1)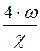 = 4 × R. (8.2)
= 4 × R. (8.2) . (8.3)
. (8.3) . (8.4)
. (8.4) . (8.5)
. (8.5) =
=  , (8.6)
, (8.6) для цилиндрических напорных труб, равный (применительно к формулам 8.4 и 8.5) 2000…2320. То есть:
для цилиндрических напорных труб, равный (применительно к формулам 8.4 и 8.5) 2000…2320. То есть: = 2000…2320.
= 2000…2320. - критическая скорость потока, при которой происходит смена режима движения жидкости.
- критическая скорость потока, при которой происходит смена режима движения жидкости.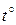 = 15 °С в открытом прямоугольном лотке, если объёмный расход жидкости Q равен 0,56 м3/с, глубина воды в лотке b = 0,7 м, а ширина лотка b = 0,8 м.
= 15 °С в открытом прямоугольном лотке, если объёмный расход жидкости Q равен 0,56 м3/с, глубина воды в лотке b = 0,7 м, а ширина лотка b = 0,8 м. - диаметр эквивалентный, м;
- диаметр эквивалентный, м; =
= 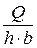 =
=  = 1,0 м/с.
= 1,0 м/с. =
=  =
=  = 1,02 м.
= 1,02 м. = 886956,52.
= 886956,52. = 2000…2320,
= 2000…2320,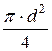 .
. .
. =
=  .
. .
. = 0,1 (м).
= 0,1 (м).


