Основное уравнение равномерного движения

Найдем общее выражение для потерь напора на трение при равномерном движении жидкости в трубах, которое справедливо и для ламинарного и для турбулентного режимов движения. При равномерном движении средняя скорость и распределение скоростей по сечению должны оставаться неизменными по длине трубопровода, поэтому равномерное движение возможно лишь в трубах постоянного сечения.

Составляя уравнение Бернулли для двух сечений трубопровода постоянного сечения (см. рис. 4.4) и учитывая, что для горизонтальной трубы z₁ = z₂ и средние скорости в сечениях равны v₁ = v₂, а из потерь напора будут только потери напора на трение h_тр, имеем:

(4.8)

Уравнение (4.8) является основным уравнением равномерного движения жидкости в трубопроводах. При известных отметках положения трубопровода (z₁ и z₂ заданы) и давления в одном из сечений это уравнение позволяет найти давление в другом сечении. Для этого нужно только определить потерянную энергию h_тр.

Рис. 4.44.4 – к выводу уравнения равномерного движения.

Основному уравнению равномерного движения жидкости в трубопроводах можно придать также другой вид. Для этого выделим в трубопроводе радиусом r₀ между сечениями 1–1 и 2 - 2 соосный цилиндр радиусом r и длиной l (рис. 4.4). На этот цилиндр со стороны окружающей жидкости действуют силы: в сечении 1-1 сила давления равная P₁ = p₁ p r², в сечении 2-2 сила давления равная P₂ = p₂ p r² и на боковую поверхность сила трения равная T = 2 p r l t. Так как движение равномерное, то сумма действующих на цилиндр сил равна нулю: P₁ - P₂ - T = 0. Уравнение динамического равновесия рассматриваемого цилиндра можно записать в виде

(4.9)

где t – сила сопротивления на единице площади поверхности жидкости цилиндра (касательное напряжение).

Разделив обе части этого уравнения на 2 л r l, получим:

.

(4.10)

Если выразить разность давлений через потери напора на трение получим:

(4.11)

Касательное напряжение распределяется по линейному закону (см. рис. 4.4) - оно равно нулю на оси трубы и принимает максимальное значение t₀ на стенке (r = r₀), где t₀= r g h_тр r₀ /(2 l). Отсюда следует:

(4.12)

Уравнение (4.11) представляет собой общее выражение для потерь напора при равномерном движении жидкости в трубопроводах круглого сечения. Это уравнение в одинаковой мере применимо как к ламинарному, так и к турбулентному режиму.

Ламинарный режим движения

Ламинарный режим движения существует в трубах, если число Рейнольдса меньше критического числа Рейнольдса Re < Re_кр = 2000¸2320. Закон Ньютона внутреннего трения для круглой трубы запишется

.

(4.13)

Подставляя касательные напряжения в уравнение равномерного движения, получим:

.

(4.14)

Разделим переменные, для этого дифференциал скорости перенесём в левую часть уравнения, а всё остальное в правую

.

(4.15)

Интегрируем это уравнение в пределах от радиуса r, где местная скорость равна u, до радиуса трубы r0. где скорость равна нулю:

,

(4.16)

Тогда распределение скорости в поперечном сечении трубы при ламинарном режиме движение происходит по параболическому закину

,

(4.17)

Расход жидкости равен сумме расходов по элементарным струйкам, имеющим площадь кольца dw = 2 p r d r

.

(4.18)

Средняя скорость в трубе равна

.

(4.19)

Из последней формулы следует, что средняя скорость в трубе при ламинарном режиме движения равна половине максимальной скорости. Из последней формулы найдем потери напора на трение

.

(4.20)

Эта формула носит название формулы Пуазейля. Из неё следует, что потери напора на трение пропорциональны средней скорости в трубе и обратно пропорциональны квадрату радиуса трубы. Но в общем случае потери напора на трение рассчитываются по формуле Дарси-Вейсбаха, поэтому сравнивая формулы (4.19) и (4.3)

(4.21)

получим значение для коэффициента гидравлического трения

(4.22)

 

Турбулентный режим движения

Турбулентный режим движения существует в трубах, если число Рейнольдса больше критического числа Рейнольдса Re > Re_кр = 2000¸2320. Турбулентный режим движения по своей природе нестационарный режим, поэтому и давления и скорости в любой точке меняются с течением времени. На рис. 4.5 приведено изменение составляющей местной скорости вдоль оси x с течением времени u_x(t). Среднее значение этой скорости за достаточно большой промежуток времени называется осреднённой скоростью

(4.23)

Разность местной скорости и осреднённой скорости называется пульсацией скорости u¢_x(t)

(4.24)

Пульсации скорости происходят как вдоль оси трубы, так и по радиусу трубы. Поэтому частицы жидкости, находящиеся у стенки трубы и имеющие маленькую скорость вдоль оси трубы могут оказаться на оси трубы, где большие скорости и будут тормозить эти слои. А частицы жидкости, находящиеся на оси трубы и имеющие большую скорость вдоль оси трубы могут оказаться у стенки трубы, где маленькие скорости и будут ускорять эти слои.

Рис. 4.54.5 – пульсации местной скорости в турбулентном потоке.

Поэтому за счет пульсаций скоростей эпюра скорости при турбулентном режиме у стенки быстро возрастает, чем при ламинарном режиме, а на оси трубы эпюра более пологая.

 

Рис. 4.64.6 – эпюры скоростей при ламинарном и турбулентном режиме

 

 

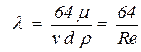
Рис. 4.74.7 – структура потока при турбулентном режиме

 

Рис. 4.84.8 – гидравлически гладкие а) и гидравлически шероховатые трубы b)