
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы кинематики и динамики жидкостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
3.1. Основные понятия и определения гидродинамики Местная скорость – u – скорость движения частицы жидкости в данной точке потока. Местная скорость зависит от координат точки x, y, z и времени t. Давление в данной точке потока p также зависит от координат этой точки и время. Поэтому
Для решения гидродинамической задачи необходимо найти распределение давления p и составляющих вектора скорости ux, uy, uz в пространстве в любой момент времени. Движение называется установившемся, если давление p и скорости u не зависит от времени. В противном случае, движение называется неустановившемся (нестационарным).
Полем скоростей называется рисунок (рис. 3.1), на котором в масштабе показаны величины векторов скоростей в различных точках потока.
Линией тока (рис. 3.2) - – называется линия, во всех точках которой вектор скорости совпадает с касательной. При установившемся движении линия тока является траекторией частицы жидкости. При неустановившемся движении траектория и линия тока не совпадают. Трубкой тока -называется поверхность, образованная линиями тока проведёнными через бесконечно малый замкнутый контур (рис. 3.3).
Свойства: Частицы жидкости не могут пересечь боковую поверхность трубки тока. Элементарная струйка - называется движения жидкости, ограниченная трубкой тока. Потоком жидкости -называется совокупность элементарных струек, скользящих друг относительно друга (рис. 3.4). Поток называется напорным, если боковая поверхность потока ограничена твёрдыми стенками, в этом случае движение происходит, в основном, за счёт перепада давления - движение в трубе. Поток называется безнапорным, если имеет поверхность, на которой давление постоянно, в этом случае движение происходит за счёт сил тяжести (движение в реке).
Движение жидкости называется равномерным (рис. 3.5), если вдоль любой линии тока величина и направление скорости не меняется, в противном случае, движение называют неравномерным (рис. 3.6).
Поперечным сечением потока w называется поверхность проведения перпендикулярно направлению скорости (рис. 3.7). На рис. 3.7 обозначения 1-1, 2-2, 3-3 являются поперечными сечениями. Свойство поперечного сечения – в поперечном сечении давление изменяется по гидростатическому закону:
Или
Некоторые виды поперечных сечений их характеристики приведены на рисунке 3.8.
Смоченным периметром c - называется часть периметра поперечного сечения, где жидкость соприкасается с твёрдыми стенами. Гидравлическим радиусом R - называют отношение площади поперечного сечения к смоченному периметру R = w/c. Эквивалентным диаметром - называется учетверённый гидравлический радиус dэ = 4 R. Эквивалентным диаметром или гидравлическим радиусом используется при расчёте движения жидкости в потоках, когда поперечное сечение не является круглой трубой. Например, при расчёте вентиляционных каналов, теплообменных аппаратов и т.д. В этом случае в формулах расчёта потерь напора по длине hд, числа Re и коэффициент гидравлического сопротивления трения l вместо диаметра D подставляется эквивалентный диаметр dэ.
При расчёте давления жидкости в каналах обычно используется гидравлический радиус. Объемным расходом Q называется объем жидкости прошедший через поперечное сечение за единицу времени.
Массовым расходом Qm называется масса жидкости прошедшая через поперечное сечение за единицу времени.
Массовый расход равен произведению плотности r на объемный расход:
Средней скоростью v называется отношение объемного расхода жидкости к площади поперечного сечения.
Если объединить последние два уравнения, получим для массового расхода выражение
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 694; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.109.141 (0.009 с.) |

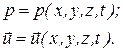
 Рис. 3.13.1 – поле скоростей
Рис. 3.13.1 – поле скоростей
 Рис. 3.23.2 – линия тока
Рис. 3.23.2 – линия тока
 Рис. 3.33.3 – Трубка тока
Рис. 3.33.3 – Трубка тока
 Рис. 3.43.4 – Поток жидкости
Рис. 3.43.4 – Поток жидкости
 Рис. 3.53.5-Равномерное движение
Рис. 3.53.5-Равномерное движение
 Рис. 3.63.6 - Неравномерное движение
Рис. 3.63.6 - Неравномерное движение
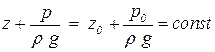 .
.
 Рис. 3.73.7 Поперечное сечение потока
Рис. 3.73.7 Поперечное сечение потока




 .
.
 .
.
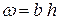 .
.
 .
.
 .
.
 .
.
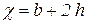 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
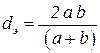 .
.
 .
.
 .
.

 .
.
 .
.
 .
.
 .
.
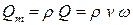 .
.



