
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приборы для измерения абсолютного, манометрического давлений и давления вакуумаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Абсолютное давление измеряется приборами, в которых имеется объем, из которого откачен воздух. Раньше атмосферное давление измерялось с помощью ртутного барометра рис. 2.5. Если стеклянную трубку, запаянную с одного конца, заполнить ртутью и открытым концом опустить в ртуть, то уровень жидкости в трубке станет равным hрт. На поверхности ртути в трубке давление равно нулю (p0 = 0). На поверхности ртути в сосуде давление равно атмосферному давлению pат. Горизонтальная поверхность, проведенная по уровню ртути в сосуде, является поверхностью равного давления. Поэтому по основному уравнению гидростатики
И тогда высота столба ртути равна
Атмосферное давление также измеряется механическими барометрами. Манометрическим давлением pм называется разность абсолютного и атмосферного давления, или избыток абсолютного давления над атмосферным давлением.
Манометрическое давление может меняться в пределах – pат < pм < ∞. Давлением вакуума pv называется разность абсолютного и атмосферного давления, или недостаток абсолютного давления над атмосферным.
Давление вакуума может меняться в пределах –∞ < pv < pат.
Сила давления жидкости на наклонную плоскую стенку Представим на рис. 2.4, а открытый сосуд, наполненный жидкостью и имеющий плоскую наклонную стенку ОМ. В плоскости этой стенки наметим оси координат Оу и Ох. Ось Ох направим перпендикулярно к плоскости чертежа.
На стенке сосуда ОМ наметим некоторую плоскую фигуру любого очертания, имеющую площадь S. Эта фигура на рис. 2.4, будет проектироваться в линию (показанную на чертеже жирно). Представим еще на рис. 2-15, б стенку сосуда ОМ, повернутую относительно оси Оу на 90° (совмещенную с плоскостью чертежа). Ясно, что на рис. 2.4 намеченная плоская фигура будет изображаться без искажения. В соответствии с первым свойством гидростатического давления можем утверждать, что во всех точках площади S давление жидкости будет направлено нормально к стенке. Отсюда заключаем, что сила абсолютного гидростатического давления pa, действующая на произвольную плоскую фигуру площадью S, будет также направлена по отношению к стенке нормально (как это показано на рис. 2.4). Поставим перед собой цель найти: а) величину силы P A абсолютного гидростатического давления; б) положение линии действия силы PA Наметим на рассматриваемой фигуре произвольную точку т, заглубленную под уровнем жидкости на величину
где У точки т выделим элементарную площадку
или согласно (2-40)
Интегрируя это выражение по всей площади
Ясно, что:
где уС - координата центра тяжести (точки С) данной плоской фигуры. Подставляя (2-79) в (2-78), получаем:
Так как где
Или
где Формулу (2.37) можно представить еще в виде:
здесь
где Как видно, сила гидростатического давления (абсолютного или избыточного), действующая на плоскую фигуру любой формы, равна площади этой фигуры, умноженной на соответствующее гидростатическое давление ( Точка
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.150 (0.006 с.) |


 .
.
 Рис. 2.62.6 -Давление жидкости на плоскую наклонную фигуру площадью S
Рис. 2.62.6 -Давление жидкости на плоскую наклонную фигуру площадью S
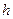 и имеющую координату
и имеющую координату 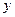 , ясно, что
, ясно, что
 - угол наклона боковой стенки сосуда к горизонту.
- угол наклона боковой стенки сосуда к горизонту.
 . Сила абсолютного гидростатического давления, действующая на эту площадку,
. Сила абсолютного гидростатического давления, действующая на эту площадку, ,
,

 , получаем:
, получаем:

 - статический момент плоской фигуры относительно оси Ох;
- статический момент плоской фигуры относительно оси Ох; .
.

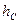 - заглубление центра тяжести
- заглубление центра тяжести  плоской фигуры под горизонтом жидкости, то
плоской фигуры под горизонтом жидкости, то ,
,
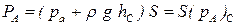 ,
,
 -абсолютное гидростатическое давление в точке, являющейся центром тяжести рассматриваемой плоской фигуры.
-абсолютное гидростатическое давление в точке, являющейся центром тяжести рассматриваемой плоской фигуры. ,
,
 - сила, обусловленная атмосферным (поверхностным) давлением, передающимся через жидкость на плоскую фигуру:
- сила, обусловленная атмосферным (поверхностным) давлением, передающимся через жидкость на плоскую фигуру: ,
,
 - сила избыточного (весового) давления:
- сила избыточного (весового) давления: ,
,
 - избыточное (весовое) давление в центре тяжести фигуры.
- избыточное (весовое) давление в центре тяжести фигуры.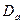 пересечения линии действия силы
пересечения линии действия силы 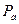 с плоскостью, в которой лежит рассматриваемая фигура, называется центром давления силы
с плоскостью, в которой лежит рассматриваемая фигура, называется центром давления силы  , этим и определится линия действия силы
, этим и определится линия действия силы 


