
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения движения материальной точки. Первая и вторая задачи динамики.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Принимая во внимание то, что ускорение точки есть вторая производная по времени от её радиуса – вектора, а сила может зависеть от времени, положения и скорости точки, равенство (4.1) можно записать в виде:
Это выражение называют дифференциальным уравнением движения свободной точки в векторной форме. Записывая его в проекциях на декартовые оси, получаем дифференциальные уравнения точки в скалярной форме.
а в проекциях на оси естественного трехгранника имеем:
Из уравнений (4.4) следует, что равнодействующая Если точка несвободная, то силу целесообразно записывать в виде:
Где Как видно из дифференциальных уравнений движения, в динамике материальной точки можно решить две задачи. Первая (прямая) задача динамики. Даны уравнения движения точки, например в координатной форме:
Требуется найти действующие на неё силы. Решение этой задачи сводится дифференцированию выражений (4.5) по времени. Вторая (обратная) задача динамики. Даны силы, действующие на точку
требуется найти закон движения точки. Решение этой задачи значительно сложнее. Оно сводится к интегрированию системы дифференциальных уравнений при соответствующих начальных условиях. Число начальных условий равно порядку системы дифференциальных уравнений, в общем случае (4.6) – шести: Задача D1 посвящена второй задаче динамики.
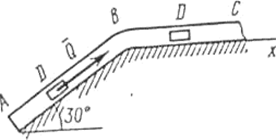
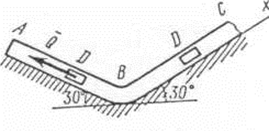
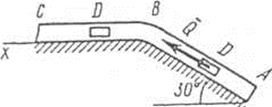
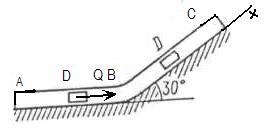
Задача Д1. Груз D массой m, получил в точке A начальную скорость На участке AB на груз кроме силы тяжести действует постоянная сила В точке B груз, не изменяя своей скорости, переходит на участок BC трубы, где на него кроме силы тяжести действуют сила трения (коэффициент трения груза о трубу Считая груз материальной точкой и зная расстояние AB = l или время
Указания. Задача Д1 – на интегрирование дифференциальных уравнений движения точки (решение второй задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке AB, учтя начальные условия. Затем, зная время движения груза на участке, определить скорость груза в точке B. Эта скорость будет начальной для движения груза на участке BC тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке B, и полагая в этот момент t = 0. При интегрировании уравнения движения на участке AB в случае, когда задана длина
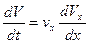 . .
Пример Д1. На вертикальном участке АВ трубы (рис. Д1) на груз D массой т действуют сила тяжести и сила сопротивления R; расстояние от точки А, где
Решение. 1. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы Р =
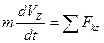 или или 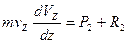 (1) (1)
Далее находим
Введем для сокращения записей обозначения
Где при подсчете принято
Разделяя в уравнении (4) переменные, а затем беря от обеих частей интегралы, получим
По начальным условиям при z = 0
В результате находим
Полагая в равенстве (6) z = l = 2,5 м и заменяя kи п их значениями (3), определим скорость v в груза в точке В (
2. Рассмотрим теперь движение груза на участке ВС; найденная скорость VB будет для движения на этом участке начальной скоростью (у0 = V B). Изображаем груз (в произвольном положении) и действующие на него силы Р — mgJ^,FJ9 и F. Проведем из точки В оси Вх и By и составим дифференциальное уравнение движения груза в проекции на ось Вх:
или
где
Разделив обе части равенства на т, вычислим
Умножая обе части уравнения (10) на dt и интегрируя, найдем
Будем теперь отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t = 0. Тогда при t = 0; v =
При найденном значении
Умножая здесь обе части на dtи снова интегрируя, найдем
Так как при t = 0 x = 0, то
где х — в метрах, t — в секундах.
Механическая система. Основные понятия. Механической системой называется совокупность материальных точек или тел, в которой движение каждой из них зависит от движения остальных. При рассмотрении механических систем различают внешние и внутренние силы. Силы действующие на точку механической системы со стороны точек (или тел) не входящих в систему, называются внешними и обозначаются В соответствии с третьим законом Ньютона, внутренние силы удовлетворяют следующим условиям. 1. Массой механической системы называется сумма масс материальных точек системы
Центром масс механической системы называется геометрическая точка, радиус – вектор которой определяется формулой.
Отсюда следует и скалярные выражения для координат центра масс.
При изучении движения твердого тела, важную роль играют моменты инерции, Моментом инерции относительно оси называется сумма произведений масс точек тела на квадраты их расстояний до этой оси.
Обычно ось, относительно которой вычисляется осевой момент инерции, указывается соответствующим индексом, например: Для определения закона движения точек механической системы на основании второго закона Ньютона можно записать.
Здесь
Вместе с тем во многих задачах в этом нет необходимости. Для описания движения достаточно знать поведение с течением времени интегральных кинетических характеристик системы, которые определяются общими теориями динамики системы.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 740; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.18.220.61 (0.011 с.) |

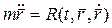 (4.2)
(4.2)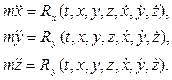 (4.3)
(4.3)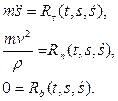 (4.4)
(4.4)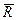 (так же как и ускорение точки
(так же как и ускорение точки  ) лежит в соприкасающейся плоскости.
) лежит в соприкасающейся плоскости.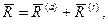
 - соответственно равнодействующие активных сил и реакций связи.
- соответственно равнодействующие активных сил и реакций связи.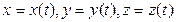 (4.5)
(4.5)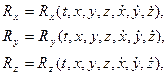 (4.6)
(4.6)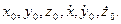
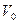 , движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 – Д1.9, табл. Д1).
, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 – Д1.9, табл. Д1).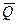 (ее направление показано на рисунках) и сила сопротивления среды
(ее направление показано на рисунках) и сила сопротивления среды  , груза (направлена против движения); трением груза о трубу на участке AB пренебречь.
, груза (направлена против движения); трением груза о трубу на участке AB пренебречь.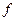 = 0.2) и переменная сила
= 0.2) и переменная сила 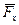 на ось x задана в таблице.
на ось x задана в таблице.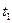 движения груза на участке BC, т.е. x =
движения груза на участке BC, т.е. x = 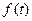 , где x = BD.
, где x = BD. участка, целесообразно перейти к переменному x, учтя, что
участка, целесообразно перейти к переменному x, учтя, что , Н
, Н
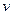 0,8
0,8 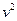 0,5
0,5  -3cos(4t)
2cos(2t)
-6sin(4t)
-3cos(4t)
2cos(2t)
-6sin(4t)
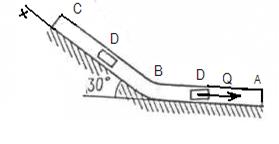
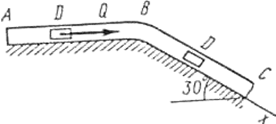

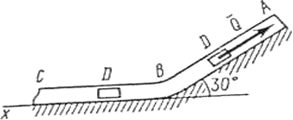
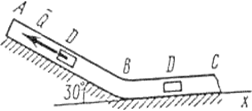
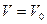 до точки В равно l. На наклонном участке ВС на груз действуют сила тяжести и переменная сила F = F(t), заданная в ньютонах.
до точки В равно l. На наклонном участке ВС на груз действуют сила тяжести и переменная сила F = F(t), заданная в ньютонах.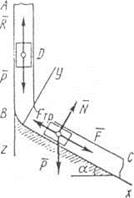 Дано: т = 2 кг, R =
Дано: т = 2 кг, R = 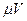 ,где
,где 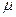 = 0,4 кг/м, V 0 = 5 м/с, l = 2,5 м, Ft = 16sin(4t). Определить: x =
= 0,4 кг/м, V 0 = 5 м/с, l = 2,5 м, Ft = 16sin(4t). Определить: x =  — закон движения груза на участке ВС.
— закон движения груза на участке ВС.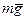 и
и 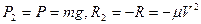 ; подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что
; подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что 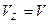 получим
получим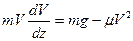 или
или  (2)
(2)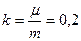
 ,
, 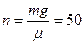
 (3)
(3)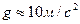 . Тогда уравнение (2) можно представить в виде
. Тогда уравнение (2) можно представить в виде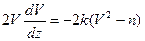 (4)
(4)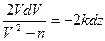 и
и 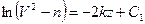 (5)
(5) =
= 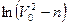 и из равенства (5) находим
и из равенства (5) находим 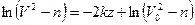 или
или 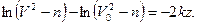 . Отсюда
. Отсюда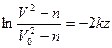 и
и 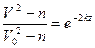
 (6)
(6) м/с, число e = 2,7):
м/с, число e = 2,7):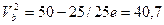 и
и 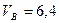 м/с (7)
м/с (7)
 (8)
(8) . Для определения N составим уравнение в проекции на ось By. Так как ау = 0, получим 0 = N —
. Для определения N составим уравнение в проекции на ось By. Так как ау = 0, получим 0 = N — 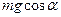 , откуда
, откуда 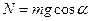 . Следовательно,
. Следовательно, 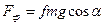 ; кроме того, Fx = 16sin(4t) и уравнение (8) примет вид
; кроме того, Fx = 16sin(4t) и уравнение (8) примет вид (9)
(9) ; 16/m =8 и подставим эти значения в (9). Тогда получим
; 16/m =8 и подставим эти значения в (9). Тогда получим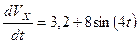 (10)
(10)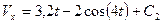 (11)
(11)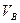 , где Уд дается равенством (7). Подставляя эти величины в (11), получим
, где Уд дается равенством (7). Подставляя эти величины в (11), получим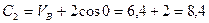
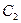 уравнение (11) дает
уравнение (11) дает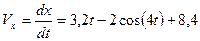 (12)
(12)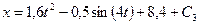 (13)
(13)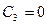 я окончательно искомый закон движения груза будет
я окончательно искомый закон движения груза будет (14)
(14)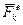 , где k – индекс соответствующей точки системы. Силы, характеризующие взаимодействие точек (или тел) самой системы называются внутренними и обозначаются
, где k – индекс соответствующей точки системы. Силы, характеризующие взаимодействие точек (или тел) самой системы называются внутренними и обозначаются  . В динамике системы активные силы, силы инерции и реакции связей соответственно обозначаются:
. В динамике системы активные силы, силы инерции и реакции связей соответственно обозначаются: 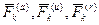 .
.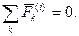 2.
2.  3.
3. 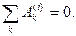 – работа внутренних сил неизменяемой системы равно нулю.
– работа внутренних сил неизменяемой системы равно нулю.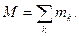 (4.7)
(4.7)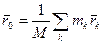 (4.8)
(4.8) (4.9)
(4.9) (4.10)
(4.10) . Момент инерции относительно центральной оси, проходящей через центр масс тела, часто обозначают
. Момент инерции относительно центральной оси, проходящей через центр масс тела, часто обозначают  .
. (k = 1,2,…,n) (4.11)
(k = 1,2,…,n) (4.11)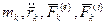 - соответственно масса ускорение k – ой точки системы, результирующая внешних и внутренних сил, приложенных в этой точке. Решение этих уравнений в общем случае оказывается трудным и громоздким, а иногда и невозможным.
- соответственно масса ускорение k – ой точки системы, результирующая внешних и внутренних сил, приложенных в этой точке. Решение этих уравнений в общем случае оказывается трудным и громоздким, а иногда и невозможным.


