
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения движения материальной точки
РАЗДЕЛ 3. ДИНАМИКА. ОСНОВНЫЕ ПОНЯТИЯ КЛАССИЧЕСКОЙ МЕХАНИКИ Динамика — раздел теоретической механики, в котором изучается движение материальных тел (точек) под действием приложенных сил. Материальное тело — тело, имеющее массу. Материальная точка — материальное тело, различие в движении точек которого является несущественным. Это может быть как тело, размерами которого при его движении можно пренебречь, так и тело конечных размеров, если оно движется поступательно. Материальными точками называют также частицы, на которые мысленно разбивается твердое тело при определении некоторых его динамических характеристик. Примеры материальных точек (рис. 1): а — движение Земли вокруг Солнца. Земля — материальная точка; б — поступательное движение твердого тела. Твердое тело — материальная точка, т. к. Инертность — свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил.
Масса тела — это скалярная положительная величина, зависящая от количества вещества, содержащегося в данном теле, и определяющая его меру инертности при поступательном движении. В классической механике масса — величина постоянная.
В динамике наряду с постоянными силами имеют место и переменные силы, которые могут зависеть от времени
Примеры таких сил приведены на рис. 3. а — 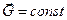 — вес тела, — вес тела,  — сила сопротивления воздуха; б — — сила сопротивления воздуха; б —  — сила тяги электровоза; в — — сила тяги электровоза; в —  — сила отталкивания от центра — сила отталкивания от центра 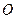 или притяжения к нему. или притяжения к нему.
Движение в механике — это изменение положения тела в пространстве и во времени. Пространство в классической механике трехмерное, подчиняющееся эвклидовой геометрии. Время — скалярная величина, одинаково протекающая в любых системах отсчета. Система единиц — это совокупность единиц измерения физических величин. Для измерения всех механических величин: достаточно трех основных единиц: единицы длины, времени, массы или силы. Все остальные единицы измерения механических величин — производные от этих. Применяются два типа систем единиц: международная система единиц СИ (или более мелкая — СГС) и техническая система единиц — МкГС. ТЕМА 1. ВВЕДЕНИЕ В ДИНАМИКУ МАТЕРИАЛЬНОЙ ТОЧКИ. 1.1. Законы динамики материальной точки (законы Галилея—Ньютона) Первый закон (закон инерции). Изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или движется равномерно и прямолинейно до тех пор, пока приложенные силы не заставят ее изменить это состояние. Движение, совершаемое точкой при отсутствии сил или под действием уравновешенной системы сил, называется движением по инерции.
Второй закон (основной закон динамики).
Произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а ее направление совпадает с направлением ускорения.
Математически этот закон выражается векторным равенством
При При
Третий закон (закон равенства действия и противодействия). Две материальные точки действуют друг на друга с силами, равными по величине и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.
Пояснение (рис. 7). Равнодействующая Вторая (обратная) задача. Зная действующие на точку силы, ее массу и начальные условия движения, определить закон движения точки или какие-либо другие ее кинематические характеристики. Начальные условия движения точки в декартовых осях — это координаты точки Решение задач этого типа сводится к составлению дифференциальных уравнений (или одного уравнения) движения материальной точки и их последующему решению путем непосредственного интегрирования или с использованием теории дифференциальных уравнений. ТЕМА 2. ВВЕДЕНИЕ В ДИНАМИКУ МЕХАНИЧЕСКОЙ СИСТЕМЫ 2.1. Основные понятия и определения Механической системой или системой материальных точек называют совокупность взаимодействующих между собой материальных точек. Примеры механических систем: 1. материальное тело, в том числе и абсолютно твердое, как совокупность взаимодействующих материальных частиц; совокупность взаимосвязанных твердых тел; совокупность планет солнечной системы и т. д. 2. Стая летящих птиц не является механической системой, т. к. между птицами нет силового взаимодействия. Свободная механическая система — система, на движение точек которой не наложено никаких связей. Например: движение планет солнечной системы. Несвободная механическая система — система, на движение точек которой наложены связи. Например: движение деталей в любом механизме, машине и т. п. Классификация сил
Классификацию сил, действующих на несвободную механическую систему, можно представить в виде следующей схемы: Внешние силы — силы, действующие на точки данной механической системы со стороны других систем.
Свойство внутренних сил
РАЗДЕЛ 3. ДИНАМИКА. ОСНОВНЫЕ ПОНЯТИЯ КЛАССИЧЕСКОЙ МЕХАНИКИ Динамика — раздел теоретической механики, в котором изучается движение материальных тел (точек) под действием приложенных сил. Материальное тело — тело, имеющее массу.
Материальная точка — материальное тело, различие в движении точек которого является несущественным. Это может быть как тело, размерами которого при его движении можно пренебречь, так и тело конечных размеров, если оно движется поступательно. Материальными точками называют также частицы, на которые мысленно разбивается твердое тело при определении некоторых его динамических характеристик. Примеры материальных точек (рис. 1): а — движение Земли вокруг Солнца. Земля — материальная точка; б — поступательное движение твердого тела. Твердое тело — материальная точка, т. к. Инертность — свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил.
Масса тела — это скалярная положительная величина, зависящая от количества вещества, содержащегося в данном теле, и определяющая его меру инертности при поступательном движении. В классической механике масса — величина постоянная.
В динамике наряду с постоянными силами имеют место и переменные силы, которые могут зависеть от времени
Примеры таких сил приведены на рис. 3. а — 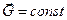 — вес тела, — вес тела,  — сила сопротивления воздуха; б — — сила сопротивления воздуха; б —  — сила тяги электровоза; в — — сила тяги электровоза; в —  — сила отталкивания от центра — сила отталкивания от центра 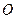 или притяжения к нему. или притяжения к нему.
Движение в механике — это изменение положения тела в пространстве и во времени. Пространство в классической механике трехмерное, подчиняющееся эвклидовой геометрии. Время — скалярная величина, одинаково протекающая в любых системах отсчета. Система единиц — это совокупность единиц измерения физических величин. Для измерения всех механических величин: достаточно трех основных единиц: единицы длины, времени, массы или силы. Все остальные единицы измерения механических величин — производные от этих. Применяются два типа систем единиц: международная система единиц СИ (или более мелкая — СГС) и техническая система единиц — МкГС.
ТЕМА 1. ВВЕДЕНИЕ В ДИНАМИКУ МАТЕРИАЛЬНОЙ ТОЧКИ. 1.1. Законы динамики материальной точки (законы Галилея—Ньютона) Первый закон (закон инерции). Изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или движется равномерно и прямолинейно до тех пор, пока приложенные силы не заставят ее изменить это состояние. Движение, совершаемое точкой при отсутствии сил или под действием уравновешенной системы сил, называется движением по инерции.
Второй закон (основной закон динамики).
Произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а ее направление совпадает с направлением ускорения.
Математически этот закон выражается векторным равенством
При При Третий закон (закон равенства действия и противодействия). Две материальные точки действуют друг на друга с силами, равными по величине и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.
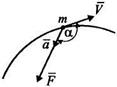
Пояснение (рис. 7). Равнодействующая Дифференциальные уравнения движения материальной точки Пусть на материальную точку действуют одновременно несколько сил, среди которых есть как постоянные, так и переменные силы. Запишем второй закон динамики в виде
Так как Проекции векторного равенства (1.2): на оси декартовых координат (рис. 8, а)
на естественные оси (рис. 8, 6)
 Уравнения (1.3) и (1.4) являются дифференциальными уравнениями движения материальной точки соответственно в декартовых осях координат и естественных осях, т. е. естественными дифференциальными уравнениями, которые обычно применяются при криволинейном движении точки, если траектория точки и ее радиус кривизны известны. Уравнения (1.3) и (1.4) являются дифференциальными уравнениями движения материальной точки соответственно в декартовых осях координат и естественных осях, т. е. естественными дифференциальными уравнениями, которые обычно применяются при криволинейном движении точки, если траектория точки и ее радиус кривизны известны.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 676; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.108.107 (0.008 с.) |
 ; в — вращение тела вокруг оси. Частица тела — материальная точка.
; в — вращение тела вокруг оси. Частица тела — материальная точка.



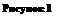



 Сила — количественная мера механического взаимодействия между телами или между телом (точкой) и полем (электрическим, магнитным и т. д.). Сила — векторная величина, характеризующаяся величиной, точкой приложения и направлением (линией действия) (рис. 2:
Сила — количественная мера механического взаимодействия между телами или между телом (точкой) и полем (электрическим, магнитным и т. д.). Сила — векторная величина, характеризующаяся величиной, точкой приложения и направлением (линией действия) (рис. 2:  — точка приложения,
— точка приложения,  — линия действия силы).
— линия действия силы).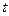 , скорости
, скорости  , расстояния
, расстояния  или от совокупности этих величин, т. е.
или от совокупности этих величин, т. е. ,
,  ,
,  ,
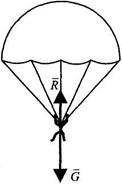
,  .
.


 Система отсчета — система координат, связанная с телом, по отношению к которому изучается движение другого тела. Инерциальная система — система, в которой выполняются первый и второй законы динамики. Это неподвижная система координат либо система, движущаяся равномерно и прямолинейно поступательно.
Система отсчета — система координат, связанная с телом, по отношению к которому изучается движение другого тела. Инерциальная система — система, в которой выполняются первый и второй законы динамики. Это неподвижная система координат либо система, движущаяся равномерно и прямолинейно поступательно. Например: движение тела по гладкой (сила трения равна нулю) горизонтальной поверхности (рис. 4:
Например: движение тела по гладкой (сила трения равна нулю) горизонтальной поверхности (рис. 4:  — вес тела,
— вес тела,  — нормальная реакция плоскости). Так как
— нормальная реакция плоскости). Так как  , то
, то 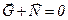 .
.
 При
При  тело движется с той же скоростью; при
тело движется с той же скоростью; при 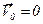 тело покоится (
тело покоится ( — начальная скорость).
— начальная скорость).

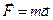 (1.1)
(1.1) — движение точки — равнопеременное (рис. 5: а — движение — замедленное,
— движение точки — равнопеременное (рис. 5: а — движение — замедленное,  ; б — движение — ускоренное,
; б — движение — ускоренное,  .
.  — масса точки,
— масса точки,  — вектор ускорения,
— вектор ускорения,  — вектор силы,
— вектор силы,  — точка движется равномерно и прямолинейно либо при
— точка движется равномерно и прямолинейно либо при  — покоится (закон инерции). Второй закон позволяет установить связь между массой тела
— покоится (закон инерции). Второй закон позволяет установить связь между массой тела  , где
, где  — ускорение свободного падения.
— ускорение свободного падения.
 Так как силы
Так как силы  приложены к разным точкам, то система сил
приложены к разным точкам, то система сил  не является уравновешенной.(рис. 6). В свою очередь
не является уравновешенной.(рис. 6). В свою очередь 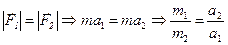 — отношение масс взаимодействующих точек обратно пропорционально их ускорениям.
— отношение масс взаимодействующих точек обратно пропорционально их ускорениям. Четвертый закон (закон независимости действия сил).
Четвертый закон (закон независимости действия сил). Ускорение, получаемое точкой при действии на нее одновременно нескольких сил, равно геометрической сумме тех ускорений, которые получила бы точка при действии на нее каждой силы в отдельности.
Ускорение, получаемое точкой при действии на нее одновременно нескольких сил, равно геометрической сумме тех ускорений, которые получила бы точка при действии на нее каждой силы в отдельности. сил
сил  определяется как
определяется как  . Так как
. Так как  и
и  , то
, то 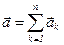 .
. ,
,  ,
,  и проекции начальной скорости
и проекции начальной скорости  на эти оси
на эти оси 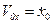 ,
, 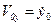 и
и  в момент времени, соответствующий началу движения точки и принимаемый равным нулю.
в момент времени, соответствующий началу движения точки и принимаемый равным нулю.
 Внутренние — силы взаимодействия между точками одной механической системы.
Внутренние — силы взаимодействия между точками одной механической системы. На произвольную точку
На произвольную точку 
 системы (рис. 1) действуют:
системы (рис. 1) действуют:  — равнодействующая внешних сил (индекс
— равнодействующая внешних сил (индекс  — первая буква французского слова exterieur — (внешний));
— первая буква французского слова exterieur — (внешний));  — равнодействующая внутренних сил (индекс
— равнодействующая внутренних сил (индекс  — от слова interieur — (внутренний)). Одна и та же сила реакции связи в зависимости от условия задачи может быть как внешней, так и внутренней.
— от слова interieur — (внутренний)). Одна и та же сила реакции связи в зависимости от условия задачи может быть как внешней, так и внутренней.
 и
и  — взаимодействующие точки механической системы (рис. 2). На основании 3-го закона динамики
— взаимодействующие точки механической системы (рис. 2). На основании 3-го закона динамики 
 С другой стороны:
С другой стороны:  . Поэтому главный вектор и главный момент внутренних сил механической системы равны нулю:
. Поэтому главный вектор и главный момент внутренних сил механической системы равны нулю: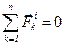 ,
,  . (2.1)
. (2.1) (1.2)
(1.2) ,
,  , где
, где  ,
,  ,
,  (1.3)
(1.3) ,
,  ,
, 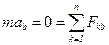 (1.4)
(1.4)




