
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетические характеристики движения механической системы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Количество движения. Количеством движения механической системы называется векторная величина
Где
Здесь Главный момент количества движения или кинетический момент механической системы. Кинетическим моментом механической системы относительно которого центра О называется векторная величина
где Момент количества движения системы относительно оси, проходящей через точку О - есть проекция вектора
Где Кинетическая энергия. Кинетическая энергия механической системы есть величина равная сумме кинетических энергий соответствующих её точек.
При вычислении кинетической энергии механической системы удобно пользоваться формулой
которая следует из теоремы Кёнига. Кинетическая энергия системы складывается из кинетической энергии центра масс и кинетической энергии системы в её движении относительно центра масс. В зависимости от характера движения тела рассмотрим следующие простейшие частные случаи: 1) Кинетическая энергия при поступательном движении, которое характеризуется
М – масса системы; 2) При вращении вокруг неподвижной оси
где 3) В случае плоскопараллельного движения
где
Общие теоремы динамики точки и механической системы. Теорема о движении центра масс системы. Центр масс механической системы движется как материальная точка, масса которой равна массе системы и к которой приложены все внешние силы, действующие на систему.
уравнение движения центра масс системы в векторной форме и в скалярной форме:
Закон сохранения движения центра масс.
Теорема об изменении количества движения материальной точки и механической системы. Для характеристики действия силы, оказываемого на тело за некоторый промежуток времени, вводится понятие об импульсе силы:
Запишем основное уравнение динамики для материальной точки с постоянной массой в форме.
Уравнение (4.23) выражает теорему об изменении количества движения точки. Интегрируя выражение (4.23) по t от 0 до t, и
Уравнение (4.24) выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на неё сил за тот же промежуток времени. Проектируя равенство (4.24) на координатные оси получим скалярные уравнения
которые используются при решении задач.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 885; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.34.50 (0.011 с.) |

 , равная геометрической сумме количеств движений всех точек системы:
, равная геометрической сумме количеств движений всех точек системы: (4.12)
(4.12) - количество движения k – ой точки. Количество движения можно представить также в следующей форме
- количество движения k – ой точки. Количество движения можно представить также в следующей форме (4.13)
(4.13) - масса системы и скорость её центра масс соответственно.
- масса системы и скорость её центра масс соответственно. , равная геометрической сумме моментов количеств движения точек системы относительно центра О.
, равная геометрической сумме моментов количеств движения точек системы относительно центра О. (4.14)
(4.14) - момент количества движения k-ой точки относительно центра О.
- момент количества движения k-ой точки относительно центра О. (4.15)
(4.15) - соответственно момент инерции тела относительно оси
- соответственно момент инерции тела относительно оси  и проекция угловой скорости на эту ось. Если система состоит из нескольких тел, вращающихся вокруг одной оси, то
и проекция угловой скорости на эту ось. Если система состоит из нескольких тел, вращающихся вокруг одной оси, то 
 (4.16)
(4.16) (4.17)
(4.17) (k = 1,2,…,n)
(k = 1,2,…,n) (4.18)
(4.18) и поэтому
и поэтому (4.19)
(4.19) - радиус вращения (расстояние до оси вращения) точки;
- радиус вращения (расстояние до оси вращения) точки; (4.20)
(4.20) - скорость центра масс,
- скорость центра масс,  - момент инерции тела относительно центральной оси. Структура формула (3.20) отражает тот факт, что плоскопараллельное движение является результатом сложения поступательного и вращательного его движения.
- момент инерции тела относительно центральной оси. Структура формула (3.20) отражает тот факт, что плоскопараллельное движение является результатом сложения поступательного и вращательного его движения. (4.21)
(4.21)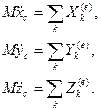 (4.22)
(4.22) , то из выражения (4.21) следует, что
, то из выражения (4.21) следует, что  или
или  . Следовательно, если сумма внешних сил равна нулю, то центр масс системы движется с постоянной скоростью (равномерно и прямолинейно). Таким образом, действие внутренних сил движения центра масс изменить не может.
. Следовательно, если сумма внешних сил равна нулю, то центр масс системы движется с постоянной скоростью (равномерно и прямолинейно). Таким образом, действие внутренних сил движения центра масс изменить не может. , то первое из этих уравнений дает
, то первое из этих уравнений дает 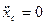 или
или  . При этом порядок системы дифференциальных уравнений снижается на единицу. Если в начальный момент
. При этом порядок системы дифференциальных уравнений снижается на единицу. Если в начальный момент 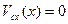 , то и в любой другой момент вращения
, то и в любой другой момент вращения 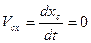 или
или  . В этом случае механическая система совершает плоскопараллельное движение. Порядок системы уравнений (4.22) снижается на две единицы.
. В этом случае механическая система совершает плоскопараллельное движение. Порядок системы уравнений (4.22) снижается на две единицы. - элементарный импульс силы;
- элементарный импульс силы;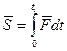 - импульс силы за конечный промежуток времени, причем
- импульс силы за конечный промежуток времени, причем и
и 

 .
. или
или  (4.23)
(4.23) от
от  до
до  , получим
, получим (4.24)
(4.24) (4.25)
(4.25)


