
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип Даламбера для механической системы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для которой точки системы запишем
Принцип. Если в любой момент времени к каждой из точек системы кроме действующих на нее внешних и внутренних сил присоединить соответствующие силы инерции, то полученная система сил будет уравновешенной. Таким образом, принцип Даламбера математически задачи динамики сводит к задачам статики о равновесии, часто упрощая соответствующие расчеты. Выражение (4.49.) суммируем по k = 1,2, …,n и умножив его слева векторно на радиусы-векторы соответствующих точек, снова суммируем по k = 1,2, …,n
Здесь Тогда из равенства (4.32.) получим
где
На основании ранее рассмотренных теорем можно записать
Следовательно, главный вектор сил инерции механической системы равен произведению массы системы на ускорение центра масс и направлен противоположно этому ускорению; главный момент сил инерции механической системы относительно центра О или оси Z равен взятой со знаком минус производной по времени кинетического момента системы относительно того центра или той же оси. Частные случаи. 1. Поступательное движение. В этом случае 2. Вращательное движение. Пусть твердое тело имеет плоскость симметрии
Если тело вращается вокруг центральной оси
симметрии и движется параллельно этой плоскости, то система сил инерции тела приводится к лежащим в плоскости симметрии силе Задача Д4 Вертикальный вал АК (рис.Д4.0 – Д4.9), вращающейся с постоянной угловой скоростью Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять a =0,6 м. Указания. Задача Д-8 – на применение к изучению движения системы принципа Даламбера. При решении задачи учесть, что когда силы инерции частиц тела (в данной задаче стержня) имеют равнодействующую



Пример Д4. Вертикальный вид длинной 3а(АВ = BD = DE = a), Закрепленный подпятником А и подшипником D (рис. Д4,а), вращается с постоянной угловой скоростью Дано: Определить: реакции подпятника А и подшипника D, пренебрегая весом вала. Решение. 1. Изображаем (с учетом заданных углов) вал и прикрепленные к нему в точках B и E стержни (рис. Д4,б). Массы и веса частей 1 и 2 ломанного стержня пропорциональны длинам этих частей и соответственно равны
2. Для определения искомых реакций рассмотрим движение заданной механической системы и применим принцип Даламбера. Проведем вращающиеся вместе с валом координатные оси Согласно принципу Даламбера, присоединим к этим силам силы инерции элементов однородного ломанного стержня и груза, считая его материальной точкой. Так как вал вращается равномерно, то элементы стержня имеют только нормальные ускорения Каждую из полученных систем параллельных сил инерции заменим ее равнодействующей, равной главному вектору этих сил. Так как модуль главного вектора сил инерции любого тела имеет значение
Сила инерции точечной массы 3 должна быть направлена в сторону, противоположную ее ускорению и численно будет равна
Ускорения центров масс частей 1 и 2 стержня и груза 3 равны:
Где
Подставив в (2) и (3) значения (4) и учтя (5), получим числовые значения
При этом линии действия равнодействующих 3. Согласно принципу Даламбера, приложенные внешние силы (активные и реакции связей) и силы инерции образуют уравновешенную систему сил. Составим для этой системы сил три уравнения равновесия. Получим
Где
Подставив в уравнения (7) соответствующие величины из равенств (1), (5), (6), (8) и решив эту систему уравнений (7), найдем искомые реакции. Ответ:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 773; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.008 с.) |

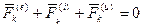 (к = 1, 2,…,4) (4.49)
(к = 1, 2,…,4) (4.49)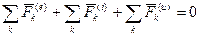 , (4.50)
, (4.50)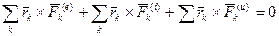
 ,
,  на основании свойств внутренних. Введем обозначения
на основании свойств внутренних. Введем обозначения 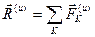 ,
, 
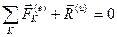 ,
,  , (4.51)
, (4.51) ,
,  – соответственно главный вектор и главный момент относительно центра О системы сил инерции.
– соответственно главный вектор и главный момент относительно центра О системы сил инерции. ,
,  ,
,  (4.52)
(4.52) . Тогда все силы
. Тогда все силы  образуют систему направленных сил и имеют равнодействующую, проходящую через центр, точку масс, точку С.
образуют систему направленных сил и имеют равнодействующую, проходящую через центр, точку масс, точку С. и вращается вокруг оси
и вращается вокруг оси  Тогда
Тогда 
 Таким образом, система сил инерции вращающегося тела, приводится к силе
Таким образом, система сил инерции вращающегося тела, приводится к силе  , определяемым формулой (4.53.)
, определяемым формулой (4.53.) , проходящей через центр масс С тела, то
, проходящей через центр масс С тела, то  = 0. Следовательно, в этом случае система сил инерции тела приводится к паре с моментом
= 0. Следовательно, в этом случае система сил инерции тела приводится к паре с моментом 

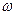 = 10
= 10  , закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (AB=BD=DE=EK=a) К валу жестко прикреплены тонкий однородный ломаный стержень массой m =10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b = 0,1 м, а их массы
, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (AB=BD=DE=EK=a) К валу жестко прикреплены тонкий однородный ломаный стержень массой m =10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b = 0,1 м, а их массы  пропорциональны длинам), и невесомый стержень длиной l = 4 b точечной массой
пропорциональны длинам), и невесомый стержень длиной l = 4 b точечной массой  = 3 кг. На конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы
= 3 кг. На конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы 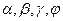 даны в столбцах 5-8.
даны в столбцах 5-8. , то численно
, то численно  , где
, где 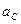 - ускорение центра масс С тела, но линия действия силы
- ускорение центра масс С тела, но линия действия силы 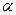 , град
, град
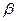 , град
, град
 , град
, град
 ,
град
,
град


 К валу жестко прикреплен в точке Е ломанный однородный стержень массой
К валу жестко прикреплен в точке Е ломанный однородный стержень массой  и длинной 10b, состоящий из двух частей 1 и 2, а в точке B прикреплен невесомый стержень длинной l = 5b с точечной массой
и длинной 10b, состоящий из двух частей 1 и 2, а в точке B прикреплен невесомый стержень длинной l = 5b с точечной массой 

 (1)
(1) так, чтобы стержни лежали в плоскости xy, и изобразим действующие на систему силы: активные силы – силы тяжести
так, чтобы стержни лежали в плоскости xy, и изобразим действующие на систему силы: активные силы – силы тяжести  и реакции связей составляющие реакции подпятника
и реакции связей составляющие реакции подпятника  и реакцию цилиндрического подшипника
и реакцию цилиндрического подшипника  .
. , направленные к оси вращения, а численно
, направленные к оси вращения, а численно  где
где  - расстояние элементов от оси вращения. Тогда силы инерции
- расстояние элементов от оси вращения. Тогда силы инерции 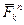 будут направлены от оси вращения, а численно
будут направлены от оси вращения, а численно  где
где 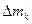 - масса элемента. Так как все
- масса элемента. Так как все 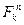 пропорционально
пропорционально  то эпюры этих параллельных сил инерции стержня образуют для части 1 треугольник, а для части 2 – прямоугольник (рис. Д4,б).
то эпюры этих параллельных сил инерции стержня образуют для части 1 треугольник, а для части 2 – прямоугольник (рис. Д4,б).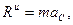 где
где 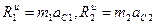 (2)
(2) (3)
(3) (4)
(4) - расстояния центров масс частей стержня от оси вращения, а
- расстояния центров масс частей стержня от оси вращения, а  - соответствующие расстояния груза:
- соответствующие расстояния груза: (5)
(5) и
и 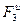 :
: (6)
(6)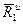 и
и  пройдут через центры тяжестей соответствующих эпюр сил инерции. Так, линия действия
пройдут через центры тяжестей соответствующих эпюр сил инерции. Так, линия действия  от вершины треугольника
от вершины треугольника  , где
, где 
 (7)
(7) - плечи сил
- плечи сил  относительно точки А, равные (при подсчетах учтено, что
относительно точки А, равные (при подсчетах учтено, что  )
)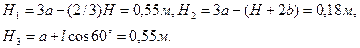 (8)
(8)



