
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Инерциальная система отсчета. Принцип относительности классической динамики.Содержание книги
Поиск на нашем сайте
Система отсчёта, в которой справедлив закон инерции: все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся. Во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму (инвариантны); в этом состоит суть механического принципа относительности или принципа относительности Галилея.
Дифференциальные уравнения движения свободной материальной точки. основное уравнение динамики можно записать так
Естественные уравнения движения свободной материальной точки. mat=åFit; man=åFin; mab=åFib (ab=0 – проекция ускорения на бинормаль), т.е.
Прямая и обратная задачи динамики. Первая или прямая задача: Известна масса точки и закон ее движения, необходимо найти действующую на точку силу.
Вторая или обратная задача: Известна масса точки и действующая на точку сила, необходимо определить закон движение этой точки.
Используя эти начальные условия можно получить шесть алгебраических уравнений для определения шести произвольных постоянных
Теорема об изменении количества движения материальной точки. Изменение количества движения материальной точки равно импульсу сил, приложенных к точке.
Теорема об изменении момента количества движения материальной точки. Производная от вектор момента количества движения относительно центра О равна сумме моментов сил, приложенных к точке относительно того же центра О.
Работа и мощность силы. Элементарная работа силы скалярная величина равная произведению элементарного перемещения на проекцию силы на это перемещение.
Мощностью силы называется величина, определяющая работу, совершаемую силой в единицу времени. В общем случае мощность равна первой производной по времени от работы.
Теорема об изменении кинетической энергии материальной точки. Изменение кинетической энергии материальной точки равно работе сил, приложенных к точке.
Принцип Даламбера для материальной точки и системы материальных точек. Уравнение движения материальной точки относительно инерциальной системы отсчета под действием приложенных активных сил и сил реакции связей имеет вид:
Силой инерции материальной точки называют произведение массы точки на вектор ускорения, взятое с обратным знаком, т.е. Если использовать понятие силы инерции, то основной закон динамики принимает вид: Принцип Даламбера. При движении материальной точки активные силы и силы реакции связей вместе с силой инерции точки образуют равновесную систему сил. Принцип Даламбера называют еще методом кинетостатики. Задачи динамики с помощью этого метода сводятся к задачам статики.
44. Общее уравнение динамики (Принцип Даламбера-Лагранжа). Пусть имеется механическая система, на которую наложены идеальные связи. Приложим ко всем материальным точкам системы реально действующие на них активные силы и реакции связей. Добавим к данным силам соответствующие силы инерции. Тогда согласно принципу Даламбера получим: , где Умножим скалярно данное уравнение на возможное перемещение
или
Записывая аналогичные уравнения для всех точек системы, складывая их почленно и учитывая, что сумма элементарных работ реакций связей для систем с идеальными связями равна нулю, получаем общее уравнение динамики
|
|||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.13.30 (0.008 с.) |

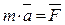
 или так
или так  . Проецируя уравнение
. Проецируя уравнение  на оси координат получаем
на оси координат получаем 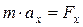

 так как
так как  ,
,  ,
,  , то
, то 


 (r – радиус кривизны траектории в текущей точке).
(r – радиус кривизны траектории в текущей точке).

 Вычисляем вторые производные по времени от координат точки, умножаем их на массу и получаем проекции силы на оси координат
Вычисляем вторые производные по времени от координат точки, умножаем их на массу и получаем проекции силы на оси координат

 Зная проекции силы на оси координат, определяем модуль силы и ее направляющие косинусы:
Зная проекции силы на оси координат, определяем модуль силы и ее направляющие косинусы:

 ,имеем шесть произвольных постоянных:
,имеем шесть произвольных постоянных:  Каждая из координат
Каждая из координат 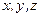 движущейся точки после интегрирования системы уравнений зависит от времени и всех шести произвольных постоянных, т.е.
движущейся точки после интегрирования системы уравнений зависит от времени и всех шести произвольных постоянных, т.е. К этим уравнениям необходимо добавить начальные условия:
К этим уравнениям необходимо добавить начальные условия: ,
, 

 ,
, 

 .
.
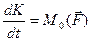


 ,
, 
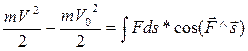
 ,
, - равнодействующая активных сил,
- равнодействующая активных сил,  - равнодействующая сил реакции связей.
- равнодействующая сил реакции связей. .
.

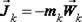
 точки k
точки k





