Приведение плоской системы сил к данному центру. Метод Пуансон.

Задача о приведении системы сил F1, F2,..., Fn к произвольном центру О, т. е. замене данной системы сил другой эквивалентной более простой, решается применением теоремы Пуансо: любая система сил F1, F2,..., Fn действующих на абсолютно твердое тело, при приведении к произвольному центру О заменяется одной силой R, равной главному вектору системы сил, приложенной в центре О и парой сил с моментом Mo, равным главному моменту системы сил относительно центра (точки) О. Главный вектор

R = F1 + F2 +... + Fn = SFk, (k = 1, 2,..., n)

а главный момент системы сил относительно центра (точки) О

Mo = m1 + m2 +... + mn= mo(F1) + mo(F2) +... + mo(Fn) = Smo(Fk). (k = 1, 2,..., n)

Величина главного вектора R не зависит от выбора центра О, а значение главного момента Mo при изменении положения центра О может в общем случае изменяться.

Для плоской системы сил F1, F2,..., Fn главный вектор R лежит в плоскости действия сил, а главный момент перпендикулярен этой плоскости (a = 90°). Поэтому главный момент плоской системы сил относительно центра О определяется как сумма алгебраических моментов сил относительно точки (центра) О

Mo = Smo(Fk), (k = 1, 2,..., n)

и изображается на плоскости дуговой стрелкой.

 

 

Частные случаи приведения плоской системы сил.

При приведении плоской системы сил возможны следующие случаи:

1. R = 0, Mo № 0:- система сил приводится к одной паре, лежащей в плоскости действия сил, с моментом Mo.

2. R № 0, Mo = 0:- система сил приводится к равнодействующей R, приложенной в точке О.

3. R № 0, Mo № 0:- система сил приводится к равнодействующей R, проходящей через точку С,положение которой определяется равенством

ОС = d = | Mo |/R, ОС ^ R.

4. R = 0, Mo = 0:

- уравновешенная система сил:

для равновесия плоской системы сил необходимо и достаточно, чтобы главный вектор этой системы сил и ее главный момент относительно любой точки были равны нулю.

 

Теорема Вариньона.

Если система сил, приложенных к абсолютно твердому телу имеет равнодействующую, то момент равнодействующей относительно произвольного центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).

Векторная запись теоремы:

 

 

Условия равновесия плоской системы пары сил.

Для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на две координатные оси и алгебраическая сумма моментов всех сил относительно произвольной точки равнялись нулю. Второй формой уравнения равновесия является равенство нулю алгебраических сумм моментов всех сил относительно любых трех точек, не лежащих на одной прямой.

F=Fk=0, М=М(Fk)=0

 

Равновесие системы тел.

 

 

Пространственная система сил. Момент силы относительно точки и оси.

Пространственная система сил. Момент силы относительно оси – скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью. Момент >0, если смотря навстречу оси, мы видим поворот, который стремится совершить сила направленный против час.стр. ,

На рис. М>0. Момент силы относительно оси равен 0: 1) если сила параллельна оси (F_xy=0), 2) если линия действия силы пересекает ось (h=0); т.е. если ось и сила лежат в одной плоскости. Аналитические выражения моментов силы относительно осей координат: М_x()=yF_z – zF_y; М_y()=zF_x – xF_z; М_z()=xF_y – yF_x.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Теорема о переносе пары сил в параллельную плоскость.

Действие пары сил на твердое тело не изменится от переноса этой пары в параллельную плоскость.

Доказательство: Пусть на твердое тело действует пара сил в плоскости 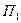. Из точек приложения сил А и В опустим перпендикуляры на плоскость 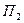и в точках их пересечения с плоскостью приложим две системы сил и 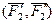, каждая из которых эквивалентна нулю.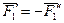

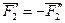
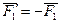
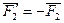
Сложим две равные и параллельные силы и 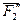. Их равнодействующая параллель-на этим силам, равна их сумме и приложена посредине отрезка 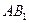в точке О. Сложим две равные и параллельные силы и . И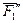х равнодействующая параллель-на этим силам, равна их сумме и приложена посредине отрезка 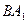в точке О. Так как , то система сил эквивалентна нулю и ее можно отбросить. Таким образом пара сил эквивалентна паре сил , но лежит в другой, параллельной плоскости.