
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение системы сил к заданному центруСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
и одной паре сил с векторным моментом относительно центра приведения O –
Здесь
В качестве центра приведения может быть выбрана любая точка в пространстве. Таким образом, замена системы сил {
Частные случаи
 , ,  , ,
В этом случае
Равновесие твердого тела Для равновесия твердого тела в пространстве, находящегося под действием произвольной системы сил, необходимо и достаточно, чтобы главный вектор и главный момент были равны нулю.
Записывая эти два векторных равенства в проекциях на оси координат, т.е. учитывая выражения (2.11) и (2.12), получим систему из шести уравнений равновесия.
Частные случаи

2 Сходящиеся силы. Необходимым и достаточным условием равновесия этой системы сил является равенство нулю её равнодействующей
3 Плоская система сил. В этом случае необходимыми и достаточными условиями равновесия являются
Уравнения равновесия для плоской системы сил можно записать в трех формах: а) первая формула непосредственно связана с условиями (2.19). С учетом выражений (2.14) можно записать
б) вторая форма уравнений равновесия получается, если одно из двух уравнений проекций в выражении (2.20) заменить уравнением моментов относительно точки, отличной от полюса A.
При этом на рисунках, чертежах прямая AB, соединяющая эти два полюса не должна быть перпендикулярна оси x. в) третья форма уравнений равновесия связана с заменой обоих уравнений проекций уравнениями моментов.
Точки A, B, C не должны лежать на одной прямой. Отметим ещё два простейших случая: 1) в случае плоской системы сходящихся сил уравнение равновесия имеет вид
2) в случае плоской системы параллельных сил
В последнем случае упрощение уравнений равновесия достигается надлежащим выбором системы координат – одну из осей координат направляют параллельно рассматриваемым силам (рис.20).
Здесь же сформулируем теорему Вариньона, которая часто используется при решении задач о равновесии. Если система сил имеет равнодействующую, то векторный момент этой равнодействующей относительно произвольно выбранного центра равен сумме векторных моментов всех сил системы относительно того же центра.
Теорема справедлива также для моментов сил относительно произвольно выбранной оси
и для моментов плоской системы сил относительно произвольно выбранного полюса
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 749; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.9.147 (0.009 с.) |

 Произвольная пространственная система сил {
Произвольная пространственная система сил {  } эквивалентна одной силе
} эквивалентна одной силе  , которая равна векторной сумме всех сил и называется главным вектором системы (рис.16),
, которая равна векторной сумме всех сил и называется главным вектором системы (рис.16), ,
, 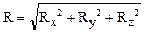 ,
, ,
,  ,
, 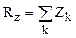 (2.11)
(2.11)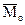 , который равен сумме векторных моментов всех сил относительно того же центра и называется главным моментом системы.
, который равен сумме векторных моментов всех сил относительно того же центра и называется главным моментом системы. ,
,  ,
, ,
,  ,
,  (2.12)
(2.12) – проекции главного вектора на декартовые оси, которые соответственно равны суммам проекций входящих в эту систему сил на эти оси;
– проекции главного вектора на декартовые оси, которые соответственно равны суммам проекций входящих в эту систему сил на эти оси; – проекции главного момента на декартовые оси, которые равны суммам моментов этих сил относительно соответствующих осей.
– проекции главного момента на декартовые оси, которые равны суммам моментов этих сил относительно соответствующих осей. и
и  называется приведением системы сил к заданному центру.
называется приведением системы сил к заданному центру. 1 Система сходящих сил эквивалентна одной равнодействующей силе {
1 Система сходящих сил эквивалентна одной равнодействующей силе {  ,
,  ,
, 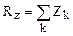 (2.13)
(2.13) 2 Плоская система приводится к главному вектору и главному моменту. Причем главный момент перпендикулярен плоскости, на которой расположена система сил, например, плоскость XOY (рис.18), т.е.
2 Плоская система приводится к главному вектору и главному моменту. Причем главный момент перпендикулярен плоскости, на которой расположена система сил, например, плоскость XOY (рис.18), т.е.  и
и  можно заменить алгебраическим моментом относительно полюса O,
можно заменить алгебраическим моментом относительно полюса O,  (см. рис.12 и 13). Таким образом, в случае плоской системы сил главный момент можно рассматривать как алгебраический момент, равный сумме моментов всех сил относительно полюса O.
(см. рис.12 и 13). Таким образом, в случае плоской системы сил главный момент можно рассматривать как алгебраический момент, равный сумме моментов всех сил относительно полюса O. ,
,  ,
, 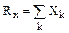 ,
,
 ,
,  (2.15)
(2.15)


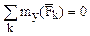 (2.16)
(2.16)

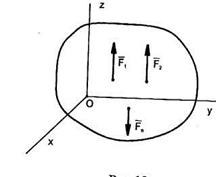 1 Равновесие пространственной системы параллельных сил. Пусть эти силы параллельны оси z. В этом случае очевидно (рис.19), что первые два и последнее уравнения (2.16) тождественно равны нулю, поэтому исключаются из рассмотрения. Уравнения равновесия имеют вид:
1 Равновесие пространственной системы параллельных сил. Пусть эти силы параллельны оси z. В этом случае очевидно (рис.19), что первые два и последнее уравнения (2.16) тождественно равны нулю, поэтому исключаются из рассмотрения. Уравнения равновесия имеют вид:
 (2.17)
(2.17) ,
, , (2.18)
, (2.18) .
. , Мо = 0 (2.19)
, Мо = 0 (2.19)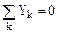 , (2.20)
, (2.20) .
.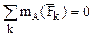 , (2.21)
, (2.21) .
.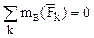 , (2.22)
, (2.22)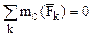 .
.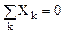
 (2.20¢)
(2.20¢)
 (2.20¢¢)
(2.20¢¢)
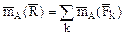 (2.23)
(2.23)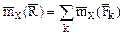 (2.24)
(2.24)


