
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ускорений точек плоской фигурыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ускорения какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки во вращательном движении плоской фигуры вокруг полюса.
 – ускорение точки А, принятой за полюс; – ускорение точки А, принятой за полюс;
где a – угол наклона относительного ускорения В случаях, когда w и e известны, формула (3.44) непосредственно используется для определения ускорений точек плоской фигуры. Однако во многих случаях зависимость угловой скорости от времени неизвестно, поэтому и угловое ускорение неизвестно. Кроме того, линия действия вектора ускорения одной из точек плоской фигуры известно. В этих случаях задача решается проектированием выражения (3.44) на соответствующим образом выбранные оси. Третий подход к определению ускорений точек плоской фигуры основан на использовании мгновенного центра ускорений (МЦУ). В каждый момент времени движения плоской фигуры в своей плоскости, если w и e не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. Эту точку называют мгновенным центром ускорений. МЦУ лежит на прямой, проведенной под углом a к ускорению точки, выбранной в качестве полюса, на расстоянии от которого
При этом угол a надо отложить от ускорения полюса
так как
Ускорение
Из формулы (3.48), (3.49) имеем
Таким образом, ускорение точек фигуры при плоском движении можно определить так же как при чистом её вращении вокруг МЦУ. Определение МЦУ. 1 В общем случае, когда w и e известны и не равны нулю, для угла a имеем
МЦУ лежит на пересечении прямых линий, проведенных к ускорениям точек фигуры под одним и тем же углом a, причем угол a нужно откладывать от ускорений точек в направлении дуговой стрелки углового ускорения (рис. 3.26).
 2 В случае w¹0, e = 0, 2 В случае w¹0, e = 0,  и, следовательно, a = 0. МЦУ лежит в точке пересечения прямых линий, по которым направлены ускорения точек плоской фигуры (рис. 3.27) и, следовательно, a = 0. МЦУ лежит в точке пересечения прямых линий, по которым направлены ускорения точек плоской фигуры (рис. 3.27)
Определение углового ускорения при плоском движении 1 Если известен угол поворота или угловая скорость в зависимости от времени, то угловое ускорение определяется по известной формуле
2 Если в указанной выше формуле
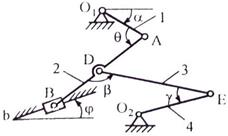
где 3 Иногда угловое ускорение удается найти путем проектирования соотношения типа (3.44) на соответствующим образом выбранные оси координат. При этом ускорение т. А, выбранной в качестве полюса, известно, известна также линия действия ускорения другой т. В фигуры. Из таким образом полученной системы уравнений определяется касательное ускорение Задача КЗ Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна В или Е (рис. К3.0 – К3.7) или из стержней 1, 2, 3 и ползунов В и E (рис. К3.8, К3.9), соединенных друг с другом и с неподвижными опорами O1, О2 шарнирами; точка D находится в середине стержня АВ. Длины стержней равны соответственно l1 = 0,4 м, l2 = 1,2 м,
Определить величины, указанные в таблицах в столбцах «Найти». Дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки (например, угол g на рис. 8 следует отложить от DB по ходу часовой стрелки, а на рис. 9 – против хода часовой стрелки и т.д.). Построение чертежа начинать со стержня, направление которого определяется углом a; ползун с направляющими для большей наглядности изобразить так, как в примере К3 (см. рис. К3б). Заданные угловую скорость и угловое ускорение считать направленными против часовой стрелки, а заданные скорость Указания. Задача К3 – на исследование плоскопараллельного движения твердого тела. При ее решения для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности. При определении ускорений точек механизма исходить из векторного равенства
Пример К3. Механизм (рис. К3а) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами O1 и О2 шарнирами. Дано: a = 60°, b = 150°, g = 90°, j = 30°, q = 30°, AD = DB, l1 = 0,4 м, l2 = 1,2м, l3 = 1,4 м, w1 = 2 с–1, e1 = 7 с–2 (направления w1 и e1 против хода часовой стрелки). Определить: vB, vE, w2, a B, e3. Решение 1 Строим положение механизма в соответствии с заданными углами
2 Определяем vB. Точка В принадлежит стержню АВ. Чтобы найти vB, надо знать скорость какой-нибудь другой точки этого стержня и направление vA = w1× l 1 = 0,8 м/с; Направление vB×cos 30° = vA×cos 60° и vB = 0,46 м/с (2) 3 Определяем
Чтобы вычислить C3D и С3В, заметим, что DAC3B – прямоугольный, так как острые углы в нем равны 30° и 60°, и что С3В = AB×sin 30° = AB×0,5 = BD. Тогда DBC3D является равносторонним и С3В = C3D. В результате равенство (3) дает vD = vB = 0,46 м/с; Так как точка Е принадлежит одновременно стержню O2E, вращающемуся вокруг O2 , то
4 Определяем w2. Так как МЦС стержня 2 известен (точка С2) и
 направлен вдоль AO1, а направлен вдоль AO1, а  – перпендикулярно АО1: изображаем эти векторы на чертеже (см. рис. К3в). Так как точка В одновременно принадлежит ползуну, то вектор – перпендикулярно АО1: изображаем эти векторы на чертеже (см. рис. К3в). Так как точка В одновременно принадлежит ползуну, то вектор  параллелен направляющим ползуна. Изображаем вектор параллелен направляющим ползуна. Изображаем вектор  на чертеже, полагая, что он направлен в ту же сторону, что и на чертеже, полагая, что он направлен в ту же сторону, что и  . Для определения . Для определения  воспользуемся равенством воспользуемся равенством
Изображаем на чертеже векторы
Таким образом, у величин, входящих в равенство (8), неизвестны только числовые значения а В и Чтобы определить а В, спроектируем обе части равенства (8) на направление ВА (ось х), перпендикулярное неизвестному вектору
Подставив в равенство (10) числовые значения всех величин из (7) и (9), найдем, что a B = 0,72 м/с2 (11) Так как получилось a B > 0, то, следовательно, вектор 6 Определяем e3. Чтобы найти e3, сначала определим
Подставив в равенство (12) числовые значения всех величии из (11) и (7), найдем, что
Ответ: vB = 0,46 м/с; vE = 0,46 м/с; w2 = 0,67 с–1; a B = 0,72 м/с2, e3 = 2,50 с–2. Примечание. Если точка В, ускорение которой определяется, движется не прямолинейно (например, как на рис. К3.0 – К3.4, где В движется по окружности радиуса О2В), то направление
При этом вектор Значение После этого в равенстве (13) остаются неизвестными только значения Найдя
ДИНАМИКА Динамика является важнейшим разделом теоретической механики, в котором изучается движение материальных тел в зависимости от действующих на них сил. В динамике на основании объективных законов и процессов устанавливаются количественные соотношения между мерами действия на материальные объекты и мерами их движения. Мерами действия между объектами являются силы, момент силы, импульс силы и работа силы, а мерами механического движения – количество движения, момент количества движения (кинетический момент) и кинетическая энергия.
Законы Ньютона – Галилея В основе динамики лежат законы Ньютона – Галилея и принцип независимости действия сил. В соответствии с первым законом постулируется существование такой системы отсчета, в которой изолированная материальная точка движется равномерно и прямолинейно или покоится. Такая система координат называется инерциальной и является основной. В соответствии со вторым законом Ньютона для свободной материальной точки можно записать:
Здесь
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 901; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.37.82 (0.008 с.) |


 (3.44)
(3.44) – ускорение т. В во вращательном движении вокруг полюса А;
– ускорение т. В во вращательном движении вокруг полюса А;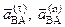 – соответственно касательная и нормальная составляющие
– соответственно касательная и нормальная составляющие 
 (3.45)
(3.45) (3.46)
(3.46) (3.47)
(3.47) и следовательно
и следовательно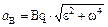 (4.48)
(4.48) (3.49)
(3.49) (3.50)
(3.50)
 3 В случае w = 0, e ¹ 0,
3 В случае w = 0, e ¹ 0, 
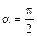 МЦУ лежит в точке пересечения перпендикуляров, восстановленных в точках А, В, С к соответствующим векторам ускорений
МЦУ лежит в точке пересечения перпендикуляров, восстановленных в точках А, В, С к соответствующим векторам ускорений  (рис. 3.28).
(рис. 3.28). (3.51)
(3.51) , Aр – расстояние от точки А плоской фигуры до МЦС, величина постоянная, то угловое ускорение определяется путем дифференцирования угловой скорости по времени
, Aр – расстояние от точки А плоской фигуры до МЦС, величина постоянная, то угловое ускорение определяется путем дифференцирования угловой скорости по времени (3.52)
(3.52) – касательно ускорение точки А.
– касательно ускорение точки А.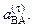 Тогда e вычисляется по известной формуле
Тогда e вычисляется по известной формуле 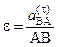 .
.









 и ускорение a B – от точки В к b (на рис. 5 – 9).
и ускорение a B – от точки В к b (на рис. 5 – 9). где А – точка, ускорение
где А – точка, ускорение  ); В –точка, ускорение
); В –точка, ускорение 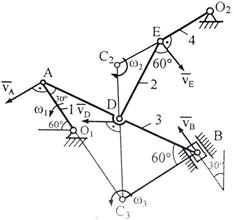


 По данным задачи, учитывая направление w1 можем определить
По данным задачи, учитывая направление w1 можем определить  численно
численно (1)
(1) и направление
и направление 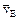 Точка Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить
Точка Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить  строим мгновенный центр скоростей (МЦС) стержня АВ; это точка С3, лежащая на пересечении перпендикуляров к
строим мгновенный центр скоростей (МЦС) стержня АВ; это точка С3, лежащая на пересечении перпендикуляров к  перпендикулярен отрезку C3D, соединяющему точки D и С3, и направлен в сторону поворота. Величину vD найдем из пропорции
перпендикулярен отрезку C3D, соединяющему точки D и С3, и направлен в сторону поворота. Величину vD найдем из пропорции (3)
(3) (4)
(4)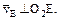 Тогда, восставляя из точек Е и D перпендикуляры к скоростям
Тогда, восставляя из точек Е и D перпендикуляры к скоростям  , построим МЦС C2 стержня DE. По направлению вектора
, построим МЦС C2 стержня DE. По направлению вектора  откуда С2E = С2D. Составив теперь пропорцию, найдем, что
откуда С2E = С2D. Составив теперь пропорцию, найдем, что vE = vD = 0,46 м/с. (5)
vE = vD = 0,46 м/с. (5)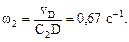 (6)
(6) 5 Определяем
5 Определяем  где численно
где численно (7) (7)
(7) (7) (8)
(8) (вдоль ВА от В к А)и
(вдоль ВА от В к А)и  (в любую сторону перпендикулярно ВА); численно
(в любую сторону перпендикулярно ВА); численно 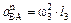 . Найдя w3 с помощью построенного МЦС С3 стержня 3, получим
. Найдя w3 с помощью построенного МЦС С3 стержня 3, получим (9)
(9)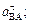 их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси.
их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси. Тогда получим
Тогда получим (10)
(10)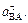 Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим
Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим (12)
(12) Знак указывает, что направление
Знак указывает, что направление 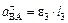 получим
получим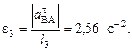
 ) и исходное уравнение (8) примет вид
) и исходное уравнение (8) примет вид (13)
(13)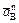 (см., например, рис. К3.0) будет направлен вдоль BO2, а вектор
(см., например, рис. К3.0) будет направлен вдоль BO2, а вектор  перпендикулярно BO2 в любую сторону. Числовые значения
перпендикулярно BO2 в любую сторону. Числовые значения 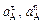 и
и  определяются так же, как в рассмотренном примере (в частности, по условиям задачи может быть
определяются так же, как в рассмотренном примере (в частности, по условиям задачи может быть 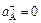 или
или  если точка А движется прямолинейно).
если точка А движется прямолинейно). также вычисляется по формуле
также вычисляется по формуле  где l – радиус окружности O2B, а vB определяется так же, как скорость любой другой точки механизма.
где l – радиус окружности O2B, а vB определяется так же, как скорость любой другой точки механизма.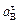 и
и  и они, как и в рассмотренном примере, находятся проектированием обеих частей равенства (13) на две оси.
и они, как и в рассмотренном примере, находятся проектированием обеих частей равенства (13) на две оси. можем вычислить искомое ускорение
можем вычислить искомое ускорение  Величина
Величина  (4.1)
(4.1)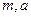 – соответственно масса и ускорение точки,
– соответственно масса и ускорение точки, 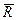 - действующая на неё сила. Если на точку действует несколько сил, то под
- действующая на неё сила. Если на точку действует несколько сил, то под 


