
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о сложении скоростейСодержание книги
Поиск на нашем сайте
При сложном движении точки абсолютная скорость равна геометрической (векторной) сумме относительной и переносной скоростей (рис. 3.13).
Модуль абсолютной скорости определяется по формуле:
В разных учебниках можно встретить следующие обозначения скоростей:
Ускорение точки в сложном движении При определении ускорений точки в сложном движении пользуются теоремой Кориолиса, по которой абсолютное ускорение точки равно сумме трех ускорений: переносного, относительного и поворотного или Кориолисова.
В общем случае, когда и переносное и относительное движения точки криволинейные, формула (3.33) приобретает вид:
где
модуль которого вычисляется:
где we – угловая скорость переносного движения, vr – относительная скорость точки. Ускорение Кориолиса равно нулю в следующих случаях: 1) если 2) если 3) если Направление ускорения Кориолиса определяем по правилу векторного произведения. Векторы
При решении каждой конкретной задачи рекомендуется соблюдать следующий порядок.
2 Выбрать неподвижную и подвижную системы координат. 3 Мысленно остановить переносное движение и определить скорость и ускорение точки в относительном движении. 4 Мысленно отвлекаясь от относительного движения, найти скорость и ускорение переносного движения точки. 5 По угловой скорости переносного движения и скорости точки в относительном движении определить Кориолисово ускорение.
7 Спроектировать векторы ускорений или их составляющих на оси координат. 8 По найденным проекциям определить искомые скорости и ускорения (модули этих векторов и их направляющие косинусы). В случаях, когда число рассматриваемых векторов не превышает трех, что имеет место при определении скоростей и в некоторых частных случаях определения ускорений, можно использовать формулы теоремы синусов и теоремы косинусов, т.е. непосредственно рассмотреть треугольники векторов скоростей и ускорений.
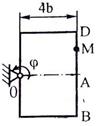
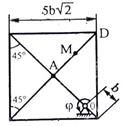
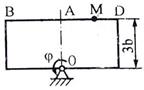
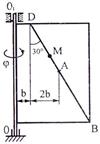
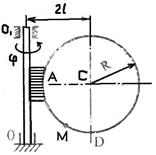
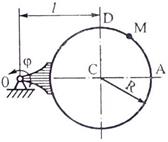
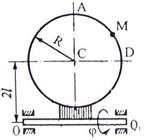
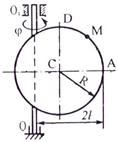
Задача К2 Прямоугольная пластина (рис. К2.0 – К2.4) или круглая пластина радиуса По пластине вдоль прямой BD (рис. 0 – 4) или по окружности радиуса R
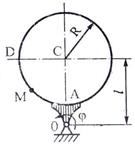
Указания. Задача К2 – на сложное движение точки. Для её решения воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка М на пластине в момент времени t1 = 1 с, и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунках к задаче). В случаях, относящихся к рис. 5 – 9, при решении задачи не подставлять числового значения R, пока не будут определены положение точки М в момент времени t1 = 1 c и угол между радиусами СМ и CA в этот момент. Рассмотрим пример решения этой задачи.
 Начало относительного движения в точке А, положительное направление отсчета s – от А к М. Начало относительного движения в точке А, положительное направление отсчета s – от А к М.
Дано: R = 0,5 м; j = t2 – 0,5t3; Определить: Решение
Найдем положение точки М1 в относительном движении и определим угловую скорость и угловое ускорение плиты при t1 = 1 c. Имеем дуговую координату
которой соответствует центральный угол
Знак (–) свидетельствует о том, что дуговую координату s1 или центральный угол y1 в момент времени t1 = 1 c. Необходимо отложить против хода часовой стрелки, т.е. точка М1 находится слева от точки А. Здесь и далее индекс "1" при символах означает, что соответствующая величина вычислена при t1 = 1 с. Имеем угловую скорость и угловое ускорение плиты:
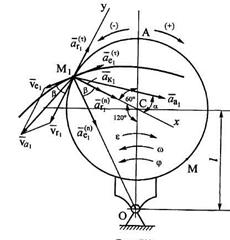
Направления
2 Определение абсолютной скорости. В момент времени t1 = 1 с по формуле (3.31) имеем:
При определении относительной скорости мысленно остановим переносное движение.
Знак (–) показывает, что вектор При определении переносной скорости мысленно остановим относительное движение, т.е. будем считать, что точка находится в положении М1, жестко связана с плитой и вместе с плитой вращается вокруг точки О.
где Модуль абсолютной скорости в момент времени t1 = 1 c найдем по теореме косинусов:
Угол b, в свою очередь, определим по теореме синусов:
Отсюда Тогда 3 Определение абсолютного ускорения. В момент времени t1 = 1 c по формуле (3.34) имеем:
Найдем касательную составляющую относительного ускорения:
Касательное ускорение есть постоянная величина и, как показывает знак
которое направлено к центру кривизны относительной траектории, т.е. к центру окружности радиуса R. Касательная и нормальная составляющие ускорения переносного движения точки определяются соответственно по формулам:
Причем Вычислим модуль Кориолисова ускорения:
где g – угол между векторами Таким образом Направление ускорения Кориолиса определяется по правилу Жуковского. При этом будем учитывать, что Модуль абсолютного ускорения получаем следующим образом. С началом в точке М1 выбираем абсолютную систему координат. Учитывая, что все векторы полученных выше ускорений лежат в одной в плоскости, в плоскости диска, достаточно выбрать двумерную систему координат. Причем оси этой системы рационально направить по взаимоперпендикулярным векторам слагаемых ускорений. Поэтому ось М1х направляем к центру окружности радиуса R, по направлению векторов
Модуль направления вектора абсолютного ускорения точки определяется по формулам:
Таким образом, абсолютная скорость точки М1 при t1 = 1 c
При этом абсолютное ускорение
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 906; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.239.63 (0.007 с.) |

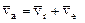 (3.31)
(3.31)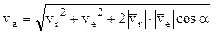 (3.32)
(3.32)
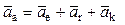 (3.33)
(3.33)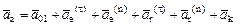 (3.34)
(3.34)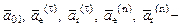 соответственно ускорения начала подвижной системы координат, касательные и нормальные составляющие переносного и относительного ускорений. В случаях, когда переносное движение представляет собой вращение вокруг неподвижной оси начало подвижной системы осей удобно поместить на оси вращения и поэтому
соответственно ускорения начала подвижной системы координат, касательные и нормальные составляющие переносного и относительного ускорений. В случаях, когда переносное движение представляет собой вращение вокруг неподвижной оси начало подвижной системы осей удобно поместить на оси вращения и поэтому 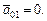 Вектор ускорения Кориолиса определяется по формуле:
Вектор ускорения Кориолиса определяется по формуле: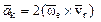 (3.35)
(3.35)
 , т.е. в случаях поступательного переносного движения или в моменты обращения в нуль угловой скорости непоступательного переносного движения;
, т.е. в случаях поступательного переносного движения или в моменты обращения в нуль угловой скорости непоступательного переносного движения; , т.е. в случаях относительного покоя точки или в моменты обращения в нуль относительной скорости точки;
, т.е. в случаях относительного покоя точки или в моменты обращения в нуль относительной скорости точки;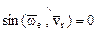 , т.е. в случаях
, т.е. в случаях 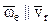 , относительная скорость параллельна оси переносного вращения.
, относительная скорость параллельна оси переносного вращения. составляют правую систему ортогональных векторов. Для определения направления ускорения Кориолиса удобно пользоваться правилом
составляют правую систему ортогональных векторов. Для определения направления ускорения Кориолиса удобно пользоваться правилом 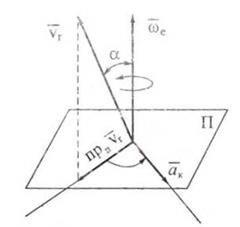 1 Разложить сложное (абсолютное) движение точки на относительное и переносное движения.
1 Разложить сложное (абсолютное) движение точки на относительное и переносное движения.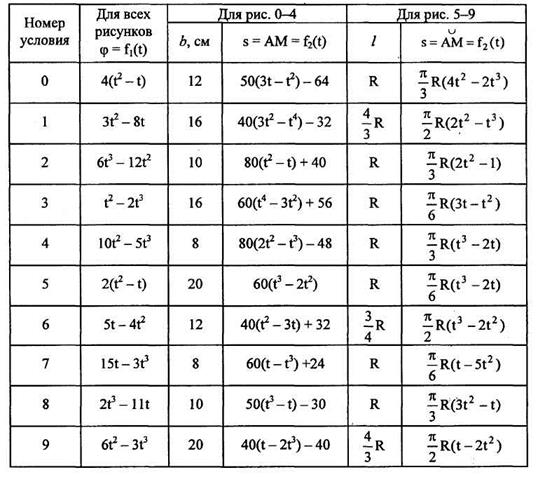

 ; (j – в радианах, s – в метрах,
; (j – в радианах, s – в метрах,  в момент времени t1 = 1 с.
в момент времени t1 = 1 с.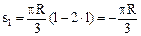 ,
,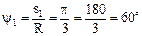
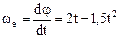 ,
,  = 2×1 – 1,5×1 = 0,5 с–1.
= 2×1 – 1,5×1 = 0,5 с–1. ,
,  = 2 – 3×1 = –1 с–2.
= 2 – 3×1 = –1 с–2.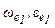 соответственно показаны на рис. К2
соответственно показаны на рис. К2

 направлен в сторону отрицательного отсчета дуговой координаты s.
направлен в сторону отрицательного отсчета дуговой координаты s.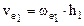
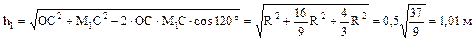 ,
,  = 0,5×1,01» 0,5 м/с.
= 0,5×1,01» 0,5 м/с.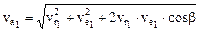 .
.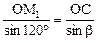
 b = 17°36¢.
b = 17°36¢.
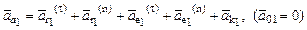
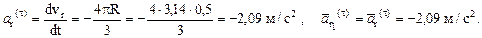
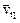 . Нормальное ускорение относительного движения равно
. Нормальное ускорение относительного движения равно ,
,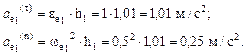
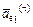 направлено по касательной к траектории переносного движения, к дуге окружности радиуса OM1 = h1 = 1,01 м; а
направлено по касательной к траектории переносного движения, к дуге окружности радиуса OM1 = h1 = 1,01 м; а 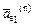 – к центру этой окружности, т.е. к точке О.
– к центру этой окружности, т.е. к точке О.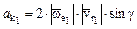
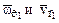 . Из рис. К2 очевидно, что g = 90°.
. Из рис. К2 очевидно, что g = 90°.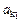 = 2×0,5×1,57×1 = 1,57 м/с2.
= 2×0,5×1,57×1 = 1,57 м/с2.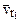 лежит в плоскости, перпендикулярной
лежит в плоскости, перпендикулярной  т.е. в плоскости диска. Тогда поворотом вектора
т.е. в плоскости диска. Тогда поворотом вектора 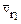 на 90° по ходу переносного вращения получим направление Кориолисова ускорения (рис. К2).
на 90° по ходу переносного вращения получим направление Кориолисова ускорения (рис. К2).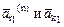 , ось М1у – по касательной к этой окружности, по направлению вектора
, ось М1у – по касательной к этой окружности, по направлению вектора  Затем все слагаемые ускорения спроектируем на эти оси. Вычислив алгебраические суммы одноименных проекций векторов ускорений, определим соответствующие проекции искомого вектора
Затем все слагаемые ускорения спроектируем на эти оси. Вычислив алгебраические суммы одноименных проекций векторов ускорений, определим соответствующие проекции искомого вектора  на эти оси.
на эти оси.
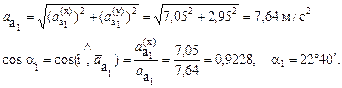
 имеет модуль
имеет модуль 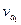 = 2,05 м/с и образует угол с осью М1у (с касательной)
= 2,05 м/с и образует угол с осью М1у (с касательной) .
.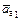 имеет модуль а а1 = 7,64 м/с2 и образует с осью М1х угол a = 22°40¢.
имеет модуль а а1 = 7,64 м/с2 и образует с осью М1х угол a = 22°40¢.


