
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ускорение точки при прямолинейном движенииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Ускорение точки при прямолинейном движении Если вектор
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным. Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное, вообще говоря, не верно) Ускорение точки при движении по окружности w = wτ + wn Тангенциальное ускорение — направлено по касательной к траектории, обозначается wτ (aτ). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.
Центростремительное или Нормальное ускорение — возникает при движении точки по окружности, обозначается wn. Является составляющей вектора ускорения w. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:
2. Зако́ны Ньюто́на — три закона, лежащие в основе классической механики и позволяющие записать уравнения движения для любой механической системы, если известны силовые взаимодействия для составляющих её тел. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год). Первый закон Ньютона Основная статья: Инерция Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела. Современная формулировка В современной физике первый закон Ньютона принято формулировать в следующем виде[1]:
Закон верен также в ситуации, когда внешние воздействия присутствуют, но взаимно компенсируются (это следует из 2-го закона Ньютона, так как скомпенсированные силы сообщают телу нулевое суммарное ускорение). Историческая формулировка Ньютон в своей книге «Математические начала натуральной философии» сформулировал первый закон механики в следующем виде:
С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает. С другой стороны, в произвольной (скажем, вращающейся) системе отсчёта закон инерции неверен. Поэтому ньютоновская формулировка нуждается в уточнениях. Второй закон Ньютона Основная статья: Второй закон Ньютона Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО). Современная формулировка
где — ускорение материальной точки; Или в более известном виде:
В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:
где — скорость точки; — время; Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:
или
Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности. Нельзя рассматривать частный случай (при) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО. Историческая формулировка Исходная формулировка Ньютона:
Третий закон Ньютона Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой, а второе — на первое с силой. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются. Современная формулировка
Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами. Историческая формулировка
Выводы Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, если потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел, то возникает закон сохранения суммарной механической энергии взаимодействующих тел:
Законы Ньютона являются основными законами механики. Из них могут быть выведены уравнения движения механических систем. Однако не все законы механики можно вывести из законов Ньютона. Например, закон всемирного тяготения или закон Гука не являются следствиями трёх законов Ньютона. Сила инерции Законы Ньютона справедливы только в инерциальных системах отсчета. Если мы честно запишем уравнение движения тела в неинерциальной системе отсчета, то оно будет по виду отличаться от второго закона Ньютона:, где - это ускорение, наблюдаемое в рассматриваемой системе отсчёта, и - ускорение данной точки этой неинерциальной системы отсчёта относительно любой инерциальной системы отсчёта. Однако часто, для упрощения рассмотрения, вводят фиктивную «силу инерции», и тогда эти уравнения движения переписываются в виде, идентичном второму закону Ньютона. Математически здесь всё корректно (правильно), но с точки зрения физики новую фиктивную силу нельзя рассматривать как нечто реальное, как результат некоторого реального воздействия на тело. Ещё раз подчеркнём: «сила инерции» — это лишь удобная параметризация того, как отличается движение в инерциальной и неинерциальной системах отсчета. Решение уравнений движения Уравнение является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию(перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости. Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.
3. Вращением твёрдого тела вокруг неподвижной оси называется такое его движение, при котором две точки тела остаются неподвижными в течение всего времени движения. При этом также остаются неподвижными все точки тела, расположенные на прямой, проходящей через его неподвижные точки. Эта прямая называется осью вращения тела.
Положение плоскости Положение тела относительно выбранной системы отсчета однозначно определяется в любой момент времени, если задано уравнение
Рис. 4-4
У тела, совершающего вращение вокруг неподвижной оси, одна степень свободы, так как его положение определяется заданием только одного параметра – угла Угол Для характеристики вращательного движения твердого тела вокруг неподвижной оси введём понятия угловой скорости и углового ускорения. Алгебраической угловой скоростью тела в какой-либо момент времени называется первая производная по времени от угла поворота в этот момент, то есть Угловая скорость является положительной величиной при вращении тела против часовой стрелки, так как угол поворота возрастает с течением времени, и отрицательной – при вращении тела по часовой стрелке, потому что угол поворота при этом убывает. Размерность угловой скорости по определению: В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернётся на угол
Алгебраическим угловым ускорением тела называется первая производная по времени от угловой скорости, то есть вторая производная от угла поворота т.е. Размерность углового ускорения по определению: Введем понятия векторов угловой скорости и углового ускорения тела.
Рис. 4-5
Если
ВРАЩАЮЩИЙ МОМЕНТ - мера внеш. воздействия на вращающееся тело, изменяющего угл. скорость вращения. В. м. равен алгебраич. сумме моментов всех действующих на вращающееся тело сил относительно оси вращения (см. Момент силы).В. м. может быть также выражен через угл. ускорение тела Результаты выполненных экспериментов можно записать в виде:
Это основное уравнение динамики вращательного движения тела: угловое ускорение вращающегося тела прямо пропорционально сумме моментов всех действующих на него сил относительно оси вращения тела и обратно пропорционально моменту инерции тела относительно этой оси вращения. Полученное уравнение аналогично по форме записи выражению второго закона Ньютона для поступательного движения тела. Ускорению поступательного движения тела а соответствует угловое ускорение вращательного движения
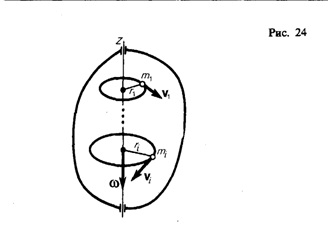
4. Слово «энергия» в переводе с греческого означает «действие». Энергичным мы называем человека, который активно двигается, производя при этом множество разнообразных действий. Энергия в физике И если в жизни энергию человека мы можем оценивать в основном по последствиям его деятельности, то в физике энергию можно измерять и изучать множеством различных способов. Ваш бодрый друг или сосед, скорее всего, откажется повторить тридцать-пятьдесят раз одно и то же действие, когда вдруг вам взбредет на ум исследовать феномен его энергичности. А вот в физике вы можете повторять почти любые опыты сколь угодно много раз, производя необходимые вам исследования. Так и с изучением энергии. Ученые-исследователи изучили и обозначили множество видов энергии в физике. Это электрическая, магнитная, атомная энергия и так далее. Но сейчас мы поговорим о механической энергии. А конкретнее о кинетической и потенциальной энергии. Потенциальная энергия В физике потенциальной энергией называют энергию, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела. То есть, если тело поднято над землей, то оно обладает возможностью падая, произвести какую-либо работу. И возможная величина этой работы будет равна потенциальной энергии тела на высоте h. Для потенциальной энергии формула определяется по следующей схеме: A=Fs=Fт*h=mgh, или Eп=mgh, где Eп потенциальная энергия тела, Причем за нулевое положение тела может быть принято любое удобное нам положение в зависимости от условий проводимых опыта и измерений, не только поверхность Земли. Это может быть поверхность пола, стола и так далее. Кинетическая энергия В случае, когда тело движется под влиянием силы, оно уже не только может, но и совершает какую-то работу. В физике кинетической энергией называется энергия, которой обладает тело вследствие своего движения. Тело, двигаясь, расходует свою энергию и совершает работу. Для кинетической энергии формула рассчитывается следующей образом: A = Fs = mas = m * v / t * vt / 2 = (mv^2) / 2, или Eк= (mv^2) / 2, где Eк кинетическая энергия тела, Из формулы видно, что чем больше масса и скорость тела, тем выше его кинетическая энергия. Каждое тело обладает либо кинетической, либо потенциальной энергией, либо и той, и другой сразу, как, например, летящий самолет. Формула энергии в физике всегда показывает, какую работу совершает или может совершить тело. Соответственно, единицы измерения энергии такие же, как и работы джоуль (1 Дж). абсолютно твердое тело (см. § 1), вращающееся около неподвижной оси z, проходящей через него (рис. 24). Мысленно разобьем это тело на маленькие объемы с элементарными массами т 1, т 2 ,..., тn, находящиеся на расстоянии r 1, r 2,..., rn от оси. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi опишут окружности различных радиусов ri, и имеют различные линейные скорости vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
или
Используя выражение (17.1), получаем
где Jz — момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела
Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела движущегося поступательно (T=mv 2/2 ), следует, что момент инерции — мера инертности тела при вращательном движении. Формула (17.2) справедлива для тела вращающегося вокруг неподвижной оси. В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:
где m — масса катящегося тела; vc — скорость центра масс тела; Jc — момент инерции тела относительно оси, проходящей через его центр масс; w — угловая скорость тела.
Гироско́п (от др.-греч. γῦρος «круг» и σκοπέω «смотрю») — устройство, способное реагировать на изменение углов ориентации связанного с ним тела относительно инерциальной системы координат, как правило, основанное на законе сохранения вращательного момента (момента импульса) поведение гироскопа описывается уравнением:
где векторы Отсюда следует, что момент силы
то есть Прецессия гироскопа Прецессия — явление, при котором момент импульса тела меняет своё направление в пространстве под действием момента внешней силы. Наблюдать прецессию достаточно просто. Нужно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем его верхняя точка постепенно опускается и движется по расходящейся спирали. Это и есть прецессия оси волчка.
Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии. С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимостью законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем. В различных разделах физики по историческим причинам закон сохранения энергии формулировался независимо, в связи с чем были введены различные виды энергии. Говорят, что возможен переход энергии одного типа в другой, но полная энергия системы, равная сумме отдельных видов энергий, сохраняется. Ввиду условности деления энергии на различные виды, такое деление не всегда может быть произведено однозначно. Для каждого вида энергии закон сохранения может иметь свою, отличающуюся от универсальной, формулировку. Например, в классической механике был сформулирован закон сохранения механической энергии, в термодинамике — первое начало термодинамики, а в электродинамике —теорема Пойнтинга. С математической точки зрения закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени. Философское значение закона. Открытие закона сохранения энергии оказало влияние не только на развитие физических наук, но и на философию XIX века. С именем Роберта Майера связано возникновение так называемого естественно-научного энергетизма — мировоззрения, сводящего всё существующее и происходящее к энергии, её движению и взаимопревращению. В частности, материя и дух в этом представлении являются формами проявления энергии. Главным представителем этого направления энергетизма является немецкий химик Вильгельм Оствальд, высшим императивом философии которого стал лозунг «Не растрачивай понапрасну никакую энергию, используй её!»
Закон сохранения и превращения энергии является одним из важнейших законов природы. Закон сохранения и превращения энергии является одним из фундаментальных законов природы и может быть сформулирован так: во всех процессах, происходящих в природе, энергия не исчезает и не создается, а переходит от одного тела к другому и превращается из одного вида в другой в эквивалентных количествах.
Закон сохранения и превращения энергии имеет глубокий философский смысл. Он блестяще подтверждает одно из основных положений диалектического материализма о том, что движение является неотъемлемым свойством материи, что оно несотворимо и неуничтожимо, а лишь преобразуется из одних форм в другие. Закон сохранения и превращения энергии строго выполняется в любых физических процессах, происходящих в природе и технике. В любом потребителе энергия переменного тока не исчезает, а лишь превращается из одной формы в другую в равной количественной мере. С помощью электродвигателя переменного тока происходит преобразование энергии электромагнитных колебаний в механическую энергию, а в лампах накаливания, в спиралях электрических плит и электрических печей электрическая энергия переменного тока преобразуется во внутреннюю энергию нагреваемых тел.
5. Внутренняя энергия включает в себя энергию всевозможных видов движений внутри системы и энергию взаимодействия всех нее частиц. Из формулы (2.2.11) Любая энергия передается в виде двух форм: теплоты и работы. Если энергия передается на молекулярном уровне, то есть в ее передаче участвуют мельчайшие частицы вещества, то это будет передача энергии в форме теплоты. Количество энергии, передаваемое при тепловом взаимодействии тел, называется количеством тепла. Понятие «количество тепла» обозначается Q, измеряется в
Если при передаче энергии наблюдается перемещение рабочего тела, то это передача энергии в форме работы. Полная работа обозначается L и измеряется в системе СИ в Удельная работа – есть полная работа отнесенная к массе вещества:
Теплота и работа имеют знак: если теплота подводится – положительный «+», если отводится– отрицательный «-». Работа, совершаемая системой под действием внешних сил при увеличении объема (dV>0) является положительной (работа расширения). Работа, совершаемая внешними силами над системой при уменьшении объема (dV<0) является отрицательной (работа сжатия). При l>0 работу совершает сам газ, при l<0 – окружающая среда.
6. Каждое тело имеет вполне определенную структуру, оно состоит из частиц, которые хаотически движутся и взаимодействуют друг с другом, поэтому любое тело обладает внутренней энергией. Внутренняя энергия — это величина, характеризующая собственное состояние тела, т. е. энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц. Внутренняя энергия одноатомного идеального газа определяется по формуле U=3/2 • т/М • RT. Внутренняя энергия тела может изменяться только в результате его взаимодействия с другими телами. Существуют два способа изменения внутренней энергии: теплопередача и совершение механической работы (например, нагревание при трении или при сжатии, охлаждение при расширении). Теплопередача — это изменение внутренней энергии без совершения работы: энергия передается от более нагретых тел к менее нагретым. Теплопередача бывает трех видов: теплопроводность (непосредственный обмен энергией между хаотически движущимися частицами взаимодействующих тел или частей одного и того же тела); конвекция (перенос энергии потоками жидкости или газа) и излучение (перенос энергии электромагнитными волнами). Мерой переданной энергии при теплопередаче является количество теплоты (Q). Эти способы количественно объединены в закон сохранения энергии, который для тепловых процессов читается так. Изменение внутренней энергии замкнутой системы равно сумме количества теплоты, переданной системе, и работы, внешних сил, совершенной над системой. D U= Q + А, где D U— изменение внутренней энергии, Q — количество теплоты, переданной системе, А — работа внешних сил. Если система сама совершает работу, то ее условно обозначают А'. Тогда закон сохранения энергии для тепловых процессов, который называется первым законом термодинамики, можно записать так: Q = Α' + D U, т. е. количество теплоты, переданное системе, идет на совершение системой работы и изменение ее внутренней энергии. При изобарном нагревании газ совершает работу над внешними силами Α' = p(V1-V2) = pΔV, где V1, и V2 — начальный и конечный объем газа. Если процесс не является изобарным, величина работы может быть определена площадью фигуры, заключенной между линией, выражающей зависимость p(V) и начальным и конечным объемом газа (рис. 13). Рассмотрим применение первого закона термодинамики к изопроцессам, происходящим с идеальным газом.
В изотермическом процессе температура постоянная, следовательно, внутренняя энергия не меняется. Тогда уравнение первого закона термодинамики примет вид: Q = А', т. е. количество теплоты, переданное системе, идет на совершение работы при изотермическом расширении, именно поэтому температура не изменяется. В изобарном процессе газ расширяется и количество теплоты, переданное газу, идет на увеличение его внутренней энергии и на совершение им работы: Q = D U + А'. При изохорном процессе газ не меняет своего объема, следовательно, работа им не совершается, т. е., А = О, и уравнение первого закона имеет вид: Q = D U, т. е. переданное количество теплоты идет на увеличение внутренней энергии газа. Адиабатным называют процесс, протекающий без теплообмена с окружающей средой. Q = 0, следовательно, газ при расширении совершает работу за счет уменьшения его внутренней энергии, следовательно, газ охлаждается, Α' = D U. Кривая, изображающая адиабатный процесс, называется адиабатой.
7. Теплоемкостью тела C называют физическую величину, численно равную количеству тепла, которое необходимо сообщить телу для нагревания его на один градус. Если сообщить телу количество тепла dQ, то температура тела повысится на dT градусов и его теплоемкость определится по формуле: C = dQ/dT. (10.8) Размерность теплоемкости равна [ C ] = Дж / К. Теплоемкость моля вещества называется молярной и обозначается символом Cm. Теплоемкость единицы массы называется удельной и обозначается c удили c, причем легко видеть. что Cm = mc уд. Теплоемкость произвольной массы m равна C = c уд m. Отсюда следует, что достаточно знать теплоемкость моля, чтобы рассчитать теплоемкость тела произвольной массы. Согласно первому началу термодинамики dQ = dU + dA. Отсюда следует, что количество тепла dQ, сообщенное телу при повышении его температуры на dT, будет затрачено не только от изменение внутренней энергии dU, но и на работу dA, которую газ при этом совершит. Так как процесс расширения газа на диаграмме p-V можно провести бесчисленным количеством способов, то теплоемкость газа может иметь такое же число значений. Для практических целей наиболее важными являются теплоемкость при постоянном давлении C p и постоянном объеме С v . Рассчитаем теплоемкость моля газа при постоянном объеме C vm. Первое начало термодинамики для изохорного процесса имеет вид dQ = dU m. Выражение (10.8) запишем в виде C vm = dU m /dT. (10.9) Учитывая формулу (10.2), получим C vm = i R /2, (10.10) где i - число степеней свободы движения молекул газа, R - универсальная газовая постоянная. Из выражения (10.10) следует, что теплоемкость C vm моля произвольного газа является постоянной величиной и зависит лишь от числа степеней свободы движения молекул. Следует однако заметить, что выражение (10.10) для воздуха не является справедливым при низких и высоких температурах (рис.10.4). При высоких температурах у молекул возбуждается колебательное движение и часть энергии теплового движения передается колебаниям атомов в молекуле. Число колебательных степеней свободы движения равно 2. При низких температурах, наоборот, наблюдается “замораживание” вращательных степеней свободы движения, объясняемое квантовой механикой. Поэтому зависимость теплоемкости от температуры имеет сложный вид.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1045; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.019 с.) |

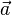 не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:
не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы: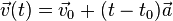
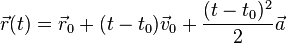 .
.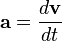
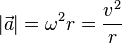
 Пусть точки A и B неподвижны. Вдоль оси вращения направим ось
Пусть точки A и B неподвижны. Вдоль оси вращения направим ось 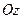 . Через ось вращения проведём неподвижную плоскость
. Через ось вращения проведём неподвижную плоскость  и подвижную
и подвижную  , скреплённую с вращающимся телом (при
, скреплённую с вращающимся телом (при 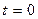
 ).
). . Угол
. Угол 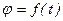 , где
, где 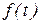 - любая дважды дифференцируемая функция времени. Это уравнение называется уравнением вращения твёрдого тела вокруг неподвижной оси.
- любая дважды дифференцируемая функция времени. Это уравнение называется уравнением вращения твёрдого тела вокруг неподвижной оси. .
.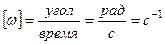
 , где n - число оборотов в минуту. Разделив этот угол на число секунд в минуте, получим
, где n - число оборотов в минуту. Разделив этот угол на число секунд в минуте, получим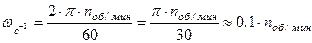

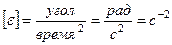
 и
и  , где
, где 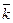 - единичный вектор оси вращения. Векторы
- единичный вектор оси вращения. Векторы 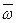 и
и 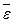 можно изображать в любых точках оси вращения, они являются скользящими векторами.
можно изображать в любых точках оси вращения, они являются скользящими векторами.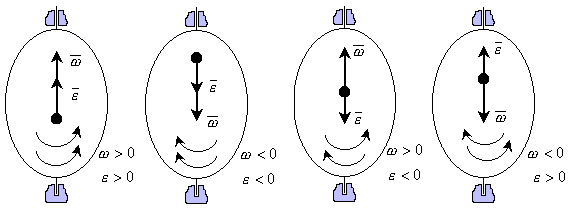
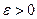 при
при 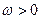 , то алгебраическая угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов
, то алгебраическая угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов  .
.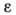 равенством
равенством 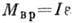 , где I - момент инерции тела относительно оси вращения.
, где I - момент инерции тела относительно оси вращения. (2.1)
(2.1) . Аналогом силы F при поступательном движении, является момент силы М во вращательном движении, а аналогом массы тела m при поступательном движении, служит момент инерции тела I при вращательном движении.
. Аналогом силы F при поступательном движении, является момент силы М во вращательном движении, а аналогом массы тела m при поступательном движении, служит момент инерции тела I при вращательном движении.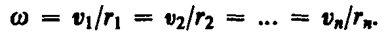 (17.1)
(17.1)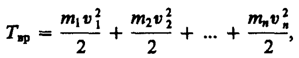
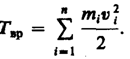
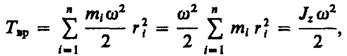
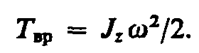 (17.2)
(17.2)
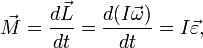
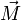 и
и 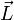 являются, соответственно, моментом силы, действующей на гироскоп, и его моментом импульса, скаляр
являются, соответственно, моментом силы, действующей на гироскоп, и его моментом импульса, скаляр 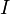 — его моментом инерции, векторы
— его моментом инерции, векторы  и
и 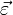 угловой скоростью и угловым ускорением.
угловой скоростью и угловым ускорением.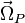 гироскопа определяется его моментом импульса и моментом приложенной силы[10]:
гироскопа определяется его моментом импульса и моментом приложенной силы[10]: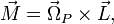
 видно, что внутренняя энергия идеального газа зависит только от его температуры, следовательно, является однозначной функцией состояния системы. Значение
видно, что внутренняя энергия идеального газа зависит только от его температуры, следовательно, является однозначной функцией состояния системы. Значение 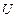 в каком-либо состоянии системы не зависит от того, каким образом система пришла в это состояние. Иначе говоря, изменение внутренней энергии
в каком-либо состоянии системы не зависит от того, каким образом система пришла в это состояние. Иначе говоря, изменение внутренней энергии 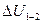 при переходе системы из состояния
при переходе системы из состояния  в состояние
в состояние  не зависит от вида процесса перехода и равно разности значений
не зависит от вида процесса перехода и равно разности значений 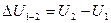 . Поэтому если в результате какого-либо процесса система возвращается в исходное состояние, то изменение ее внутренней энергии равно нулю:
. Поэтому если в результате какого-либо процесса система возвращается в исходное состояние, то изменение ее внутренней энергии равно нулю: 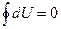 . Следовательно, элементарное изменение внутренней энергии является полным дифференциалом.
. Следовательно, элементарное изменение внутренней энергии является полным дифференциалом. или
или  (1 ккал = 4,19 кДж). Количество теплоты, отнесенное к массе вещества, называется удельной теплотой:
(1 ккал = 4,19 кДж). Количество теплоты, отнесенное к массе вещества, называется удельной теплотой: , [Дж/кг] (1.8)
, [Дж/кг] (1.8)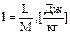 (1.9).
(1.9).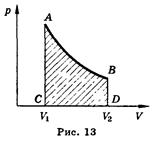
 Рассмотрим теплоемкость при постоянном да
Рассмотрим теплоемкость при постоянном да 


