
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика вращательного движения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ВВЕДЕНИЕ
Физика принадлежит к числу фундаментальных наук, и без знания её основ невозможна успешная инженерная деятельность ни в одной области современной техники. Изуче- ние физики позволяет также формировать интеллектуальные качества, необходимые специалисту для самостоятельной творческой работы. Однако освоение курса физики требует от студента – заочника огромных усилий, длительной и кропотливой работы с различными учебниками и пособиями. Для оказания помощи в изучении первой части курса физики и написано данное пособие, включающее основы механики, молекулярную физику и термодинамику, электродинамику и законы постоянного тока. Теоретический материал представлен в кратком изложе- нии и доступной форме, основное внимание при этом обращается на физическую сущность основных понятий и законов. Наряду с теоретическими основами в пособии рассматриваются практические приёмы решения типовых задач. В конце пособия представлен фонд контрольных зада- ний с таблицами вариантов контрольных работ. В приложе- ниях даются некоторые сведения из математики, а также основные справочные данные.
Выписка из типовой программы дисциплины Физика за 2011 год (1 семестр) Введение Физика в системе естественных наук. Общая структура и задачи дисциплины «Физика». Экспериментальная и теоретическая физика. Физические величины, их измерение и оценка погрешностей. Системы единиц физических величин. Краткая история физических идей, концепций и открытий. Физика и научно-технический прогресс. Механика. Кинематика. Основные кинематические характеристики криволиней- ного движения: скорость и ускорение. Нормальное и тангенциальное ускорение. Кинематика вращательного движения: угловая скорость и угловое ускорение, их связь с линейной скоростью и ускорением. Динамика. Инерциальные системы отсчета и первый закон Ньютона. Второй закон Ньютона. Масса, импульс, сила. Уравнение движения материальной точки. Третий закон Ньютона и закон сохранения импульса. Закон всемирного тяготения. Силы сопротивления. Момент импульса. Момент импульса материальной точки и механической системы. Момент силы. Уравнение моментов. Закон сохранения момента импульса механической системы. Энергия. Сила, работа и потенциальная энергия. Консервативные и неконсервативные силы. Работа и кинетическая энергия. Закон сохранения полной механической энергии в поле потенциальных сил. Динамика вращательного движения. Основное уравнение динамики вращательного движения твердого тела с закрепленной осью вращения. Момент импульса тела. Момент инерции. Формула Штейнера. Кинетическая энергия вращающегося твердого тела. Элементы механики сплошных сред. Общие свойства жидкостей и газов. Стационарное течение идеальной жидкости. Уравнение Бернулли. Идеально упругое тело. Упругие напряжения и деформации. Закон Гука. Модуль Юнга. Коэффициент Пуассона. Релятивистская механика. Принцип относительности и преобразования Галилея. Экспериментальные обоснования специальной теории относи- тельности. Постулаты специальной теории относительности (СТО) Эйнштейна. Относительность одновременности и преобразования Лоренца. Сокращение длины и замедление времени в движущихся системах отсчета. Релятивистский импульс. Взаимосвязь массы и энергии. СТО и ядерная энергетика.
Термодинамическое равновесие и температура. Нулевое начало термодинамики. Эмпирическая температурная шкала. Квазистатические процессы. Уравнение состояния в термодинамике. Обратимые и необратимые процессы. Первое начало термодинамики. Теплоемкость. Уравнение Майера. Изохорический, изобарический, изотермический, адиабати- ческий процессы в идеальных газах. Преобразование теплоты в механическую работу. Цикл Карно и его коэффициент полезного действия. Энтропия. Молекулярно-кинетическая теория. Давление газа с точки зрения МКТ. Теплоемкость и число степеней свободы молекул газа. Распределение Максвелла для модуля и проекций скорости молекул идеального газа. Экспериментальное обоснование распреде- ления Максвелла. Распределение Больцмана и барометри- ческая формула. Элементы физической кинетики. Явления переноса. Диффузия, теплопроводность, внутреннее трение. Броуновское движение.
Электростатика. Закон Кулона. Напряженность и потенциал электростатического поля. Теорема Гаусса в интегральной форме и ее применение для расчета электрических полей. Проводники в электрическом поле. Равновесие зарядов в проводнике. Основная задача электростатики проводников. Эквипотенциальные поверх- ности и силовые линии электростатического поля между проводниками. Электростатическая защита. Емкость провод- ников и конденсаторов. Энергия заряженного конденсатора. Диэлектрики в электрическом поле. Электрическое поле диполя. Диполь во внешнем электри- ческом поле. Поляризация диэлектриков. Ориентационный и деформационный механизмы поляризации. Вектор электри- ческого смещения (электрической индукции). Диэлектричес- кая проницаемость вещества. Электрическое поле в однород- ном диэлектрике. Постоянный электрический ток. Сила и плотность тока. Уравнение непрерывности для плотности тока. Закон Ома в интегральной и дифференциаль- ной формах. Закон Джоуля-Ленца. Закон Видемана-Франца. Электродвижущая сила источника тока. Правила Кирхгофа.
Методические указания
Студенту заочнику рекомендуется: 1. Прослушать курс установочных лекций по физике. На основании полученных рекомендаций продолжить самостоя- тельное изучение теоретического материала, соответствую- щего рабочей программе по физике для данной специальности. В качестве основной литературы целесообразно использовать один из рекомендуемых учебников (см. список литературы). В качестве дополнительного материала можно использовать теоретическое введение в настоящем пособии. 2. После изучения очередного раздела теории внимательно ознакомиться с примерами решения типовых задач, представленных в данном пособии. Решение задач помогает уяснить физический смысл явлений, закрепляет в памяти основные формулы, прививает навыки практического применения теоретических знаний. Типовые задачи в пособии подобраны так, что содержат элементы задач, предлагаемых для контрольных работ. Разбор их решения несомненно поможет при выполнении контрольного задания. 3. Решение контрольных задач должно сопровож- даться исчерпывающими, но краткими объяснениями. Прежде всего необходимо сделать чертёж, поясняющий содержание задачи. Затем указать основные законы и формулы, на которых базируется решение задачи. Числовые значения подставляются только в окончательную формулу, выражающую искомую величину. При этом все вычисления следует проводить в системе СИ, руководствуясь правилом приближённых вычислений. Наконец, при записи ответа численные значения следует представить в стандартном виде, т.е. как произведение десятичной дроби с одной значащей цифрой перед запятой на соответствующую степень при основании десять. Например, вместо 1350 надо записать 1,35·103, вместо 0, 0386 записать 3,86·10-2 и т.д. 4. Студент должен решить контрольные задачи того варианта, номер которого совпадает с последней цифрой его зачетки (шифра). Контрольные работы выполняются в обыч- ной школьной тетради, (каждую работу в отдельной тетради), на обложке которой приводятся сведения об исполнителе по следующему образцу: Контрольная работа по физике №1 студента группы РК-001 Шифр 257320 Иванова Петра Ивановича Контрольные работы, представленные без соблюдения указанных правил, а также работы, выполненные не по своему варианту, зачитываться не будут. Если контрольная работа не зачтена, студент обязан представить её на повторную рецензию, включив в неё те задачи, решение которых оказалось неверным. Зачтённые контрольные работы предъявляются экзаменатору. Студент должен быть готов дать во время экзамена пояснения по существу решения задач, входящих в его контрольные работы. МЕХАНИКА Механика изучает законы движения материальных объектов и те причины, которые вызывают или изменяют это движение. Основные законы механики установлены для физических моделей, к которым относятся материальная точка и абсолютно твердое тело. Материальная точка– это тело, размерами которого в условиях данной задачи можно пренебречь. Абсолютно твердое тело – это тело, деформа- цией которого в условиях данной задачи можно пренебречь. Абсолютно твердое тело можно рассматривать как систему материальных точек, жестко связанных между собой. Примеры решения задач по кинематике Пример 1. Движение частицы в плоскости ХУ описы- вается кинематическими уравнениями: Решение 1) Для нахождения уравнения траектории движения частицы необходимо исключить параметр
Полученное уравнение представляет собой уравнение параболы. 2) Вектор скорости частицы в момент времени
где Дифференцируя уравнения
и, следовательно, Модуль вектора скорости равен
Вектор ускорения представляет собой первую производ- ную от вектора скорости
где Следовательно, Знак «-» в полученном выражении свидетельствует о том, что ускорение направлено в сторону, противоположную оси У.
Модуль ускорения равен
3) Вектор средней скорости определяется выражением
где
Окончательно,
Пример 2. Камень брошен с вышки в горизонтальном направлении со скоростью υ = 30 м/c. Определить скорость, тангенциальное и нормальное ускорение камня в конце третьей секунды после начала движения. Решение Движение горизонтально брошенного тела под действием силы тяжести состоит из равномерного движения в горизон- тальном направлении со скоростью υx и свободного падения в вертикальном направлении со скоростью
Вектор полного ускорения тела
Как следует из рисунка, модуль нормального ускорения an тела равен: Тогда с учётом (1) получим
Модуль тангенциального ускорения
Выполняя вычисления, получим
Пример 3. Маховик, вращающийся с постоянной частотой Решение При равнозамедленном вращательном движении уравнения угловой скорости и углового пути имеют вид:
Решение этой системы уравнений дает соотношение, связывающее угловое ускорение с начальной
или Но так как
Подставив числовые значения в выражение (4), найдём
Угловое ускорение получилось отрицательным, так как маховик вращался замедленно. Продолжительность торможения определяем из уравнения (1):
С учетом (4) окончательно получим
Подставив числовые значения, найдем: Твердого тела Основными динамическими характеристиками абсолют- но твердого тела при вращательном движении являются момент инерции и момент импульса. Примеры решения задач по динамике поступательного и вращательного движения тел Пример 1. В системе, показанной на рисунке, массы тел равны
Решение Укажем все силы, действующие на грузы. Если считать нити, связывающие грузы, невесомыми и нерастяжимыми, а также пренебречь массой блоков, то силы натяжения нити с обеих сторон от каждого блока равны, в частности,
Выразим из уравнения (2) силу Т, получим
Приравняв правые части выражений (1) и (3), найдём
Откуда
Запишем уравнения движения грузов m1 и m2 в проекциях на ось oy:
Решая систему уравнений с учётом (4), получим
Пример 2. Моторная лодка массой m = 400 кг начинает двигаться по озеру. Сила тяги мотора F = 0,2 кН. Считая силу сопротивления пропорциональной скорости, определить скорость лодки через t = 20 с после начала её движения. Коэффициент сопротивления Решение На лодку в горизонтальном направлении действуют две силы: сила тяги мотора и сила сопротивления, величина которой пропорциональна скорости, т.е.
Для решения данного дифференциального уравнения разделим переменные
и выполним интегрирование:
Подставив пределы интегрирования, проведём преобразование
или
Окончательно получим
Произведя вычисления, найдем υ = 6.3 м /с. Пример 3. Через блок в виде диска массой m0 перекинута нить, к концам которой прикреплены грузы массами m1 и m2 (m2 > m1). Найти ускорение грузов. Трением пренебречь. Решение
На каждый из движущихся грузов действуют две силы: сила тяжести Уравнения движения этих тел в проекции на ось y имеют вид -m1a = m1g-T1, (1) m2a = m2g-T2. (2) Вращение блока вызывается действием сил натяжения нити, поскольку моменты сил тяжести блока и реакции оси равны нулю. Тогда основное уравнение динамики вращатель- ного движения для блока имеет вид
где R - радиус блока, Учтено также, что по третьему закону Ньютона силы натяжения нити с каждой из сторон блока одинаковы по модулю, т.е.
Если нить не проскальзывает относительно блока, то касательное ускорение его точек, соприкасающихся с нитью, равно ускорению нити в любой её точке, а следовательно а =εR. Решение системы полученных уравнений дает искомый результат
Пример 4. Однородный шар скатывается без скольже- ния с наклонной плоскости, образующей с горизонтом угол Решение На шар действует сила тяжести
 , (1) , (1)
где а – ускорение центра масс шара, Учитывая, что
Решая уравнения (1) и (3) совместно, получим
Примеры решения задач на работу и мощность Пример 1. Потенциальная энергия частицы имеет вид
Решение Используя выражение, связывающее потенциальную энергию частицы с силой, действующей на неё, получим
Работа сил потенциального поля равна убыли потенциальной энергии
По известным координатам точек M и N находим
Пример 2. Частица совершает перемещение в плоско- сти ХУ из точки с координатами (1,2) м в точку с координатами (2,3) м под действием силы Решение Элементарная работа, совершаемая силой
Работа при перемещении частицы из точки 1 в точку 2 определится интегрированием
Подставляя числовые значения, получим
Пример 3. Тело массой m =1,0 кг падает с высоты h =20 м. Пренебрегая сопротивлением воздуха найти среднюю мощность, развиваемую силой тяжести на пути h, и мгновен- ную мощность на высоте h/ 2. Решение Средняя мощность Nср , развиваемая силой тяжести на пути h, определяется выражением
Запишем выражение координаты y(t) тела от времени при свободном падении с высоты h с нулевой начальной скоростью:
где g – ускорение свободного падения. Полное время t падения тела с высоты h определим из этого выражения при условии y = 0: Среднее значение скорости равно
тогда
Мгновенная мощность, развиваемая силой тяжести на высоте h/ 2, равна
Расстояние, пройденное телом за промежуток времени t1, равно
откуда Мгновенная скорость υ1 тела на высоте h /2, равна
Тогда
Выполняя вычисления, получим
Пример 4. Маховиквращается по закону, выражаемому уравнением Решение Средняя мощность по определению
где t- время торможения до полной остановки, А- работа, совершаемая за это время. Работа при вращательном движении
С учётом основного уравнения динамики вращательного движения M=Iε, получим
где Время торможения до остановки найдём из условия
откуда С учётом значений t, найдём После интегрирования (2) получим абсолютное значение работы сил торможения
Подставляя (3) в (1) найдём
Законы сохранения
Любое тело (или совокупность тел) представляет собой, по существу, систему материальных точек. Состояние системы характеризуется одновременным заданием координат и скоро- стей всех ее частиц.При движении системы ее состояние изменяется со временем. Существуют, однако, такие функции координат и скоростей, образующих систему частиц, которые способны сохраняться во времени. К ним относятся энергия, импульс и момент импульса. В соответствии с этим имеют место три закона сохране- ния – закон сохранения энергии, закон сохранения импульса и закон сохранения момента импульса, которые выполняются в замкнутых системах. Система называется замкнутой, если она не обменивается с другими телами, не входящими в эту систему, соответ- ственно энергией, импульсом, моментом импульса. Законы сохранения энергии, импульса и момента импульса можно получить исходя из основных уравнений динамики, однако, следует иметь в виду, что эти законы обладают гораздо большей общностью, чем законы Ньютона, и должны рас- сматриваться как самостоятельные фундаментальные принци- пы физики, относящиеся к основным законам природы. Законы сохранения являются эффективным инструмен- том исследования. С помощью законов сохранения можно без решения уравнения движения получить ряд важнейших данных о протекании механических процессов.
Закон сохранения импульса
Импульс системы
Изменение импульса системы, согласно законам динамики, равно результирующему вектору импульса внешних сил:
В соответствии с этим уравнением, импульс системы может изменяться под действием только импульса внешних сил. Импульсы внутренних сил не могут изменить импульс системы. Отсюда непосредственно вытекает условие замкнутости системы
Примеры решения задач на законы сохранения Пример 1. Пуля массой m =15 г, летящая с горизон- тальной скоростью Решение
После удара, пренебрегая силами сопротивления воздуха, можно воспользо- ваться законом сохранения механической энергии
Решая совместно полученные уравнения, найдем
Пример 2. Шар массой m 1= 8 кг движется со скоро- стью υ1 = 2 м/с и сталкивается с шаром массой m2 = 4 кг, который движется ему навстречу со скоростью υ2 = 5 м/с. Найти скорость шаров после прямого центрального удара. Удар считать абсолютно упругим. Решение При абсолютно упругом ударе выполняются законы сохранения импульса и механической энергии:
где u1 и u 2 скорости шаров после упругого удара.
Направления векторов скоростей шаров послу удара выберем произвольно и проведем ось x параллельно векторам скорости. В проекциях на ось x закон сохранения импульса примет вид:
или
Закон сохранения механической энергии можно представить в виде или Из этого уравнения с учётом (1) получим:
откуда
Подставляя полученное выражение (2) в (1), получим:
Далее найдём
Подставим полученное выражение (3) в (2):
после преобразования найдём
Выполним вычисления:
Пример 3. Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направ- лении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью υ1 = 600 м/с, а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью υ2 = 580 м/с. С какой скоростью откатилось при этом орудие? Решение Система “орудие - снаряд” является замкнутой, поэтому можно применить закон сохранения импульса. Так как в начальный момент система покоилась, то импульс системы в процессе взаимодействия должен быть равен нулю. Пусть υ1 – скорость снаряда без отката орудия, υ2 – скорость снаряда с откатом орудия, u – скорость отката орудия, m1 – масса снаряда, m2 – масса орудия, тогда закон сохранения импульса имеет вид: m1υ2 – m2u = 0, откуда
Работа пороховых газов идёт на увеличение кин
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 735; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.17.3 (0.014 с.) |

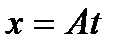 ;
; 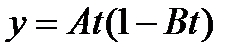 , где А и В – константы. Определить: 1) уравнение траектории
, где А и В – константы. Определить: 1) уравнение траектории 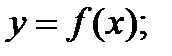 2) векторы скорости, ускорения и их численные значения; 3) вектор средней скорости за первые t секунд движения и его модуль.
2) векторы скорости, ускорения и их численные значения; 3) вектор средней скорости за первые t секунд движения и его модуль.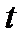 из кинематиче- ских уравнений:
из кинематиче- ских уравнений: .
. ,
,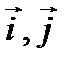 - единичные векторы вдоль осей Х и У, а
- единичные векторы вдоль осей Х и У, а 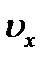 и
и 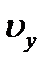 - проекции вектора скорости на соответствующие оси.
- проекции вектора скорости на соответствующие оси.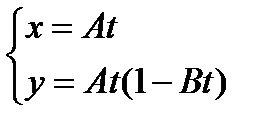 по времени, получим:
по времени, получим: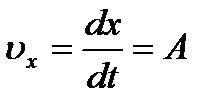 ;
; 
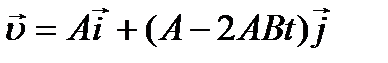 .
. .
.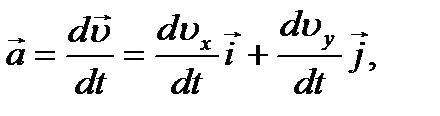
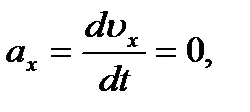
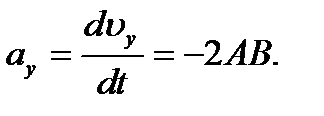
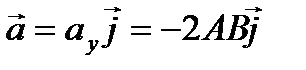 .
.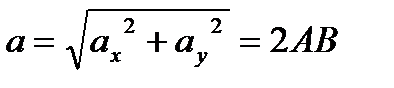 .
.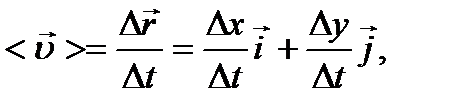
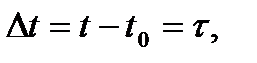 поскольку
поскольку 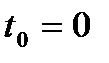 ,
, 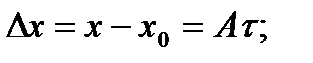
 .
.
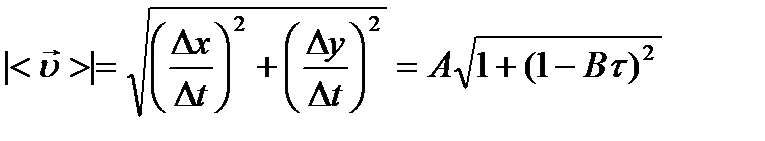 .
.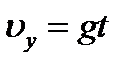 . Мгновенная скорость
. Мгновенная скорость 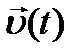 движения тела определяется сложением векторов
движения тела определяется сложением векторов 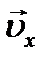 и
и 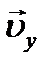 . Модуль скорости
. Модуль скорости 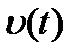 определим в соответ- ствии с теоремой Пифагора
определим в соответ- ствии с теоремой Пифагора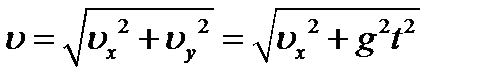 . (1)
. (1)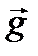 (ускорение свобод- ного падения) равен векторной сумме тангенциального
(ускорение свобод- ного падения) равен векторной сумме тангенциального 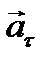 и нормального
и нормального  ускорений.
ускорений. .
.
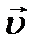
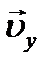
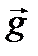
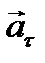
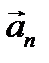
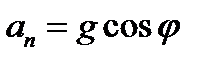 , где φ угол между векторами
, где φ угол между векторами  .
.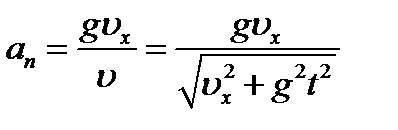 . (2)
. (2)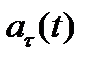 определим в соответствии с теоремой Пифагора:
определим в соответствии с теоремой Пифагора: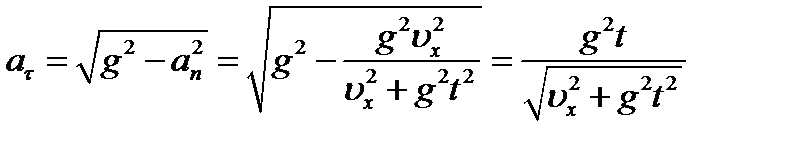 . (3)
. (3)

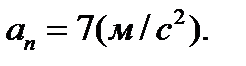
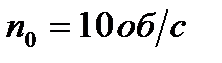 , при торможении начал вращаться равно- замедленно. Когда торможение прекратилось, частота враще- ния оказалась равной
, при торможении начал вращаться равно- замедленно. Когда торможение прекратилось, частота враще- ния оказалась равной  . Определить угловое ускоре- ние e маховика и продолжительность
. Определить угловое ускоре- ние e маховика и продолжительность  .
. , (1)
, (1)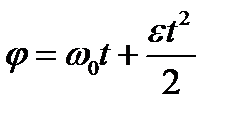 . (2)
. (2)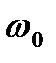 и конечной
и конечной 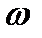 угловыми скоростями
угловыми скоростями ,
,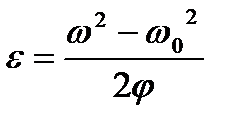 . (3)
. (3)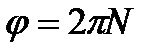 и
и 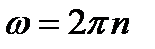 , то
, то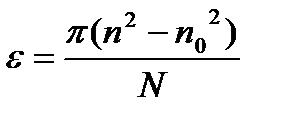 . (4)
. (4)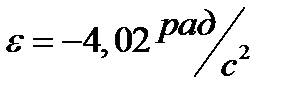 .
.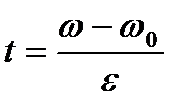 .
.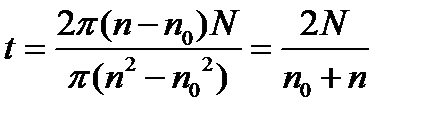 .
.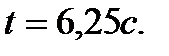
 , трения нет, массы блоков пренебрежимо малы. Найти ускорение тела массой
, трения нет, массы блоков пренебрежимо малы. Найти ускорение тела массой  относительно стола и ускорения грузов m1 и m2 относительно подвижного блока.
относительно стола и ускорения грузов m1 и m2 относительно подвижного блока.







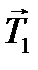







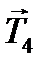

 ,
,  . Выберем положительные направления координатных осей х и y, запишем в скалярном виде уравнения движения груза
. Выберем положительные направления координатных осей х и y, запишем в скалярном виде уравнения движения груза  и системы грузов
и системы грузов  в соответствии со вторым законом Ньютона:
в соответствии со вторым законом Ньютона: ; (1)
; (1) . (2)
. (2)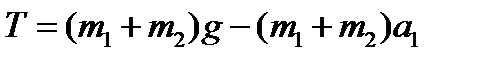 . (3)
. (3) .
. . (4)
. (4)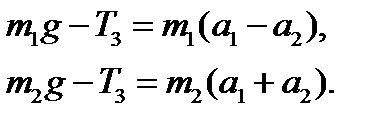
 .
. = 20 кг/с.
= 20 кг/с. . Уравнение движения лодки имеет вид:
. Уравнение движения лодки имеет вид: .
.
 .
.
 .
. .
.







 и сила натяжения нити
и сила натяжения нити  (см. рис.).
(см. рис.). , (3)
, (3)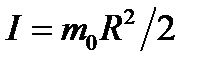 - его момент инерции, ε - угловое ускорение.
- его момент инерции, ε - угловое ускорение. .
.
 . Найдите ускорение центра инерции шара.
. Найдите ускорение центра инерции шара. , сила реакции
, сила реакции  и сила трения
и сила трения  . Последняя является силой трения покоя, которая и создает вращающий момент относительно мгновен- ной оси, проходящей через центр инерции. Под действием этих сил шар участвует в двух движениях (поступательном и вращательном), уравнения которых имеют следующий вид
. Последняя является силой трения покоя, которая и создает вращающий момент относительно мгновен- ной оси, проходящей через центр инерции. Под действием этих сил шар участвует в двух движениях (поступательном и вращательном), уравнения которых имеют следующий вид


 , (2)
, (2) - момент инерции шара относительно его центра масс,
- момент инерции шара относительно его центра масс, 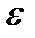 - угловое ускорение.
- угловое ускорение. ,
,  и
и  , преобразуем уравнение (2) к виду
, преобразуем уравнение (2) к виду . (3)
. (3) . (4)
. (4) , где а – константа. Найти: а) силу
, где а – константа. Найти: а) силу  , действую- щую на частицу; б) работу А, совершаемую над частицей силами поля при её перемещении из точки М (1,1,1,) в точку N (2,2,3).
, действую- щую на частицу; б) работу А, совершаемую над частицей силами поля при её перемещении из точки М (1,1,1,) в точку N (2,2,3).
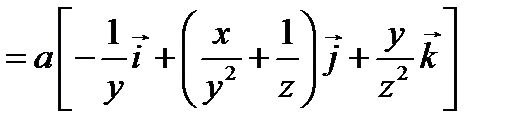 .
. .
. ,
,  ,
,  .
. Н. Определить работу данной силы.
Н. Определить работу данной силы. при перемещении
при перемещении  , равна скалярному произведению этих векторов
, равна скалярному произведению этих векторов .
. .
. .
.
 ,
, , откуда
, откуда 
 ,
, .
.
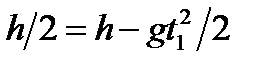 ,
,




 , где А = 2 рад, В = 32 рад/с, С = -4 рад/с2. Найти среднюю мощность
, где А = 2 рад, В = 32 рад/с, С = -4 рад/с2. Найти среднюю мощность  , развиваемую силами, действующими на маховик при его вращении, до остановки, если момент инерции I = 100 кг·м2.
, развиваемую силами, действующими на маховик при его вращении, до остановки, если момент инерции I = 100 кг·м2. , (1)
, (1) .
. , (2)
, (2) - угловое ускорение,
- угловое ускорение,  - углы поворота при t = 0 и в момент остановки.
- углы поворота при t = 0 и в момент остановки. .
. ,
,
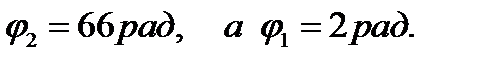
 (3)
(3)
 равен векторной сумме импульсов ее отдельных частиц, т.е.
равен векторной сумме импульсов ее отдельных частиц, т.е. , (1.60) где
, (1.60) где 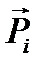 - импульс i -й частицы.
- импульс i -й частицы. . (1.61)
. (1.61) и закон сохранения импульса: импульс замкнутой механической системы остается постоянным:
и закон сохранения импульса: импульс замкнутой механической системы остается постоянным: . (1.62)
. (1.62)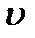 =500 м/с, попадает в баллистический маятник M = 6 кг и застревает в нем. Определить высоту h, на которую поднимется маятник после удара.
=500 м/с, попадает в баллистический маятник M = 6 кг и застревает в нем. Определить высоту h, на которую поднимется маятник после удара.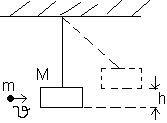 При неупругом ударе выполняется только закон сохранения импульса, в соответствии с которым
При неупругом ударе выполняется только закон сохранения импульса, в соответствии с которым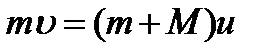 .
.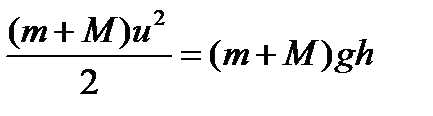 .
.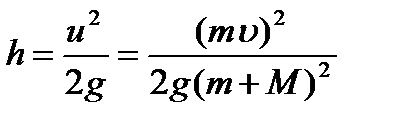 ; h = 7,9 см.
; h = 7,9 см.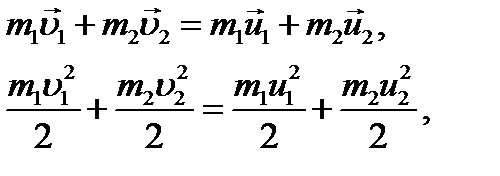
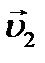
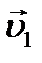
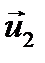
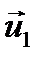
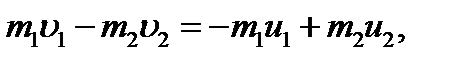
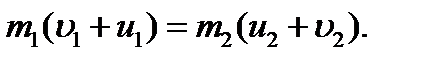 (1)
(1)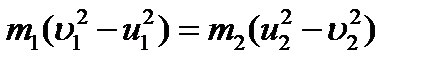 ,
,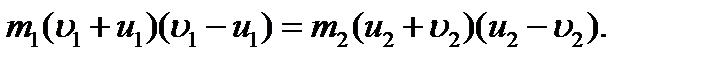
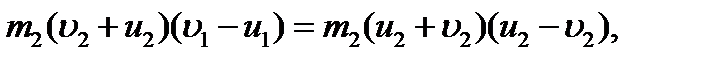
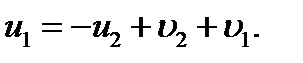 (2)
(2)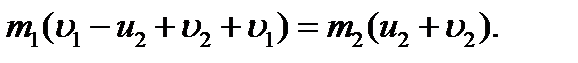
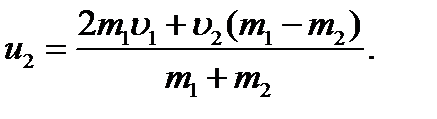 (3)
(3)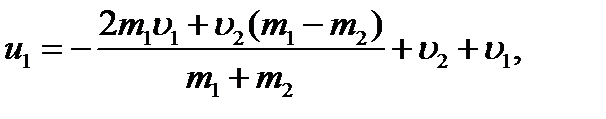
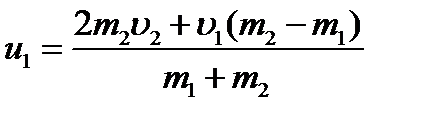 .
.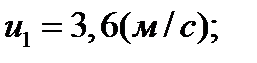
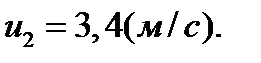
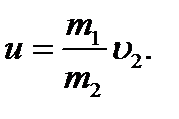 (1)
(1)


