Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение динамики вращения твердого телаСодержание книги
Поиск на нашем сайте Момент инерции. Твердое тело можно представить в виде системы жестко связанных между собой материальных точек.
Теорема Штейнера. Момент инерции тела Момент силы. Момент силы относительно точки Уравнение динамики твердого тела, вращающегося вокруг неподвижной оси: Вопрос 15.3 Основной закон динамики вращательного движения твердого тела новной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела где F – сила, приложенная к телу массой m; а – линейное ускорение тела. Если к твердому телу массой m в точке А (рис. 5) приложить силу F, то в результате жесткой связи между всеми материальными точками тела все они получат угловое ускорение где где mi – масса i- й точки; Умножая левую и правую части уравнения (1.7) на ri, получают где Плечом силы называют кратчайшее расстояние от оси вращения “ОО” (рис. 5) до линии действия силы
Рис. 5. Твердое тело, вращающееся под действием силы F около оси “ОО” Выражение (1.8) можно записать так: Просуммируем левую и правую части (1.9) по всем точкам тела: Обозначим Уравнение (1.10) – основной закон динамики вращательного движения твердого тела. Величина Мгновенное значение углового ускорения где Если в выражение основного закона (1.10) поставить значение мгновенного ускорения (1.11), то где Поэтому основной закон динамики вращательного движения твердого тела формулируется так: “Импульс момента силы Вопрос 16
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 446; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.006 с.) |

 .
.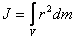 .
.
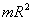
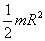




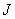 относительно любой оси вращения равен моменту инерции
относительно любой оси вращения равен моменту инерции 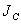 относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы
относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы 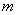 тела на квадрат расстояния
тела на квадрат расстояния  между осями:
между осями:  .
. .
. на эту ось.
на эту ось. .
. лежит в плоскости перпендикулярной оси вращения, то проекция момента силы на ось равна произведению величины силы на плечо. Плечо силы — это длина перпендикуляра, опущенного на прямую, вдоль которой направлена сила.
лежит в плоскости перпендикулярной оси вращения, то проекция момента силы на ось равна произведению величины силы на плечо. Плечо силы — это длина перпендикуляра, опущенного на прямую, вдоль которой направлена сила.
 ,
,  .
.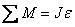 .
.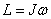 , уравнение динамики твердого тела можно представить в виде
, уравнение динамики твердого тела можно представить в виде .
.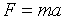 , (1.6)
, (1.6) и соответственные линейные ускорения, как если бы на каждую точку действовала сила
и соответственные линейные ускорения, как если бы на каждую точку действовала сила 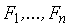 . Для каждой материальной точки можно записать:
. Для каждой материальной точки можно записать: ,
,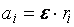 , поэтому
, поэтому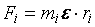 , (1.7)
, (1.7)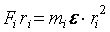 , (1.8)
, (1.8)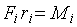 – момент силы – это произведение силы
– момент силы – это произведение силы  на ее плечо
на ее плечо 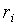 .
.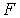 .
.
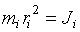 – момент инерции i -й материальной точки.
– момент инерции i -й материальной точки.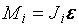 . (1.9)
. (1.9) .
. через М, а
через М, а  через J, тогда
через J, тогда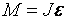 (1.10)
(1.10)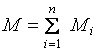 – геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение
– геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение 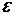 .
.  – алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение».
– алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение».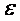 , есть первая производная угловой скорости
, есть первая производная угловой скорости  по времени
по времени  , то есть
, то есть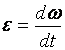 , (1.11)
, (1.11) – элементарное изменение угловой скорости тела за элементарный промежуток времени
– элементарное изменение угловой скорости тела за элементарный промежуток времени 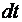 .
. или
или 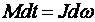 , (1.12)
, (1.12) – импульс момента силы – это произведение момента силы
– импульс момента силы – это произведение момента силы 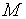 на промежуток времени
на промежуток времени 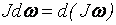 – изменение момента импульса тела,
– изменение момента импульса тела, 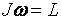 – момент импульса тела есть произведение момента инерции J на угловую скорость
– момент импульса тела есть произведение момента инерции J на угловую скорость 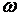 , а
, а 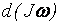 есть
есть  .
.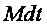 , действующий на вращательное тело, равен изменению его момента импульса
, действующий на вращательное тело, равен изменению его момента импульса  ”:
”: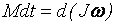 или
или