
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Адиабатический и политропный процессы. Ур. Адиабт проц.Содержание книги
Поиск на нашем сайте
Адиабатическим называется процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой. Адиабатическим процессами можно считать все быстропротекающие процессы. Таковым, например, можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько большая по значению, что обмен энергией между средой и волной произойти не успевает. Адиабатические процессы происходят в двигателях внутреннего сгорания (сжатие и расширение горючей смеси в цилиндрах), в холодильных установках и т. д. Из первого начала термодинамики (δQ=dU+δA) для адиабатического процесса следует, что
т. е. внешняя работа совершается за счет изменения внутренней энергии системы. Используя формулы δA=pdV и CV=dUm/dT, для произвольной массы газа перепишем уравнение (1) в виде
применив дифференцирование уравнение состояния для идеального газа pV=(m/M)RT получим
Исключим из (2) и (3) температуру Т.
Разделив переменные и учитывая, что Сp/СV=γ, найдем
Проинтегрируя это уравнение в пределах от p1 до p2 и соответственно от V1 до V2, и потенцируя, придем к выражению
Так как состояния 1 и 2 выбраны произвольно, то можно записать
Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона. Для перехода к переменным Т, V или p, Т исключим из (55.4) с помощью уравнения Менделеева-Клапейрона
соответственно давление или объем:
Выражения (4) — (6) представляют собой уравнения адиабатического процесса. В них безразмерная величина
называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i =3, γ=1,67. Для двухатомных газов (Н2, N2, О2 и др.) i =5, γ=1,4. Значения γ, вычисленные по формуле (55.7), хорошо подтверждаются экспериментом. Диаграмма адиабатического процесса (адиабата) в координатах р, V есть гипербола (рис. 1). На рисунке видно, что адиабата (pVγ = const) более крута, чем изотерма (pV = const) по причине, что при адиабатическом сжатии 1—3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.
Рис.1
Вычислим работу, которую совершает газ в адиабатическом процессе. Запишем уравнение (1) в виде
Если газ адиабатически расширяется от объема V1 до V2, то его температура уменьшается от T1 до T2 и работа расширения идеального газа
Используя те же приемы, что и при выводе формулы (5), выражение (8) для работы при адиабатическом расширении можно привести к виду
где p1V1=(m/M)RT1 Работа, которую совершает газом при адиабатическом расширении 1—2 (определяется площадью, заштрихованной на рис. 2), меньше, чем при изотермическом, по причине, что при адиабатическом расширении осуществляется охлаждение газа, тогда как при изотермическом — температура поддерживается постоянной за счет притока извне такого же количества теплоты. Рассмотренные изобарный, изохорный, изотермический и адиабатический процессы имеют общую особенность — они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны СV и Сp, в изотермическом процессе (dT=0) теплоемкость равна ±∞, в адиабатическом (δQ=0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается неизменной, называется политропным. Исходя из первого начала термодинамики при условии постоянства теплоемкости (C=const) можно вывести уравнение политропы:
где n=(С—Сp)/(С—СV)—показатель политропы. Очевидно, что при С=0, n=γ, из (55.9) получается уравнение адиабаты; при С = 0, n = 1 — уравнение изотермы; при С=Сp, n=0 —уравнение изобары, при С=СV, n=±∞ — уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса. Вопрос 49 Круговой процесс Циклом или круговым процессом называется совокупность термодинамических процессов, возвращающих систему в первоначальное состояние. Число таких процессов может быть любым.
На термодинамической поверхности цикл графически изображается замкнутым контуром, вид которого всецело определяется числом и формой составляющих цикл процессов. На рис. 1 изображен цикл D-E-F-D, состоящий из трех процессов: D-E, E-F и F-D. Последовательное перемещение по этим кривым приводит в исходную точку, т. е. к восстановлению первоначального состояния системы. Графическое изучение циклов, изображенных в пространственной системе координат, было бы еще более трудным, чем отдельных процессов. Поэтому и в этом случае используется тот же метод, что и при изучении процессов, т. е. цикл проектируется и изучается на одной из координатных плоскостей в сочетании с уравнением состояния. Проекцию D' E' F' D' на плоскость v-p также принято называть циклом. Следует отметить, что координатная плоскость v-p при изучении циклов имеет важное значение. Циклы графически изображаются на плоскости в координатах p – v, T – s или i-s. Если цикл совершается по часовой стрелке, то он называется прямым, если против – то обратным. Прямой цикл характерен для тепловых двигателей, обратный цикл — для холодильных машин и тепловых насосов. Машина, работающая по тепловому циклу, всегда работает при определенном перепаде температур. Это означает, что для работы такой машины необходимо иметь, по крайней мере, два источника теплоты, из которых один с более высокой температурой и другой с меньшей температурой. В термодинамике источник теплоты с более высокой температурой, от которого машина получает теплоту, принято называть горячим или высшим, а источник с меньшей температурой — холодным (часто холодильником)или низшим. В машинах – двигателях: -в координатах p – v площадь c1a2d равна положительной работе цикла в процессе подвода теплоты от горячего источника, а c1b2d – работе, затраченной на сжатие при возврате из состояния 2 в состояние 1 и отводе теплоты к холодному источнику.
Если цикл совершается против часовой стрелки(холодильный цикл), то направления потоков теплоты q1 и q2 меняются на противоположные по отношению к прямому циклу. В холодильной машине теплота, переданная горячему источнику, равна сумме теплоты, отведённой от холодного источника, и теплоты, эквивалентной механической работе, затраченной на осуществление цикла.
Особенностью диаграмм в координатах Ts является то, что линии адиабат являются перпендикулярами к оси s, а изотермы – к оси Т. Поэтому в этих координатах точки А и В соответствуют минимальному и максимальному значению энтропии s. Наглядны также точки минимальной и максимальной температур цикла. Изменение внутренней энергии u и энтальпии i в любом цикле равны нулю. Работа цикла lо соответствует площади, заключенной внутри замкнутого контура цикла, причем в прямом цикле работа положительна, а в обратном цикле - отрицательна. Обозначим q1 количество тепла, заимствованного 1 кг рабочего тела от внешнего (или верхнего) источника тепла и через q2 — количество тепла, отданного 1 кг рабочего тела внешнему охладителю (или нижнему источнику). В координатах T-s (рис. 2.) поступление q1 начинается в точке А, где контура касается линия адиабаты, и заканчивается в точке В (тепловой цикл). Отвод q2 , соответственно, происходит между точками В и А. Таким образом, в точках А и В поток теплоты меняет знак. В координатах T – s площадь A1A1BB1 равна подведённой к рабочему телу теплоте q1, а площадь A1A2BB1 - отведённой к холодному источнику теплоте q2. Площадь, заключенная внутри замкнутого контура цикла представляет собой величину работы за один цикл lо, причемработа положительна, если цикл совершается по часовой стрелке, и отрицательна, если он совершается против часовой стрелки. В любом случае lо= q1 - q2. В прямом цикле это полезно использованное в цикле тепло, в обратном – затраченная работа на осуществление цикла. Вопрос 50 Энтропия Термодинамическая энтропия {\displaystyle S}, часто именуемая просто энтропией, — физическая величина, используемая для описаниятермодинамической системы, одна из основных термодинамических величин. Энтропия является функцией состояния и широко используется в термодинамике, в том числе технической (анализ работы тепловых машин и холодильных установок) и химической (расчёт равновесий химических реакций).
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.54.147 (0.007 с.) |

 (1)
(1) (2)
(2) (3)
(3)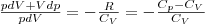

 или
или 
 (4)
(4)
 (6)
(6)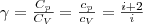 (7)
(7)

 (8)
(8)
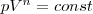 (9)
(9)





