
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи для контрольных заданийСодержание книги
Поиск на нашем сайте
1. Движение материальной точки задано уравнением x = At + Bt2, где А = 4 м/с, В = – 0,05 м/с2. Определить момент времени, в который скорость точки равна нулю. Найти координату и ускорение в этот момент. 2. Путь, пройденный точкой по окружности радиусом 2 м, выражен уравнением S = A + Bt + Ct2. Найти нормальное, тангенциальное и полное ускорения точки через время, равное 0,5 с после начала движения, если С = 3 м/с2, В = 1 м/с. 3. Точка движется по окружности так, что зависимость пути от времени дается уравнением S = A + Bt + Ct2, где В = – 2 м/с, С = 1 м/с2. Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорения через t1 =3 c после начала движения, если известно, что нормальное ускорение точки при t2 =2 c равно 0,5 м/с2. 4. Материальная точка движется прямолинейно. Уравнение движения имеет вид x = At + Bt3, где А = 3 м/с, В = 0,06 м/с3. Найти скорость и ускорение точки в моменты времени t = 0 и t = 3 с. Каковы средние значения скорости и ускорения за первые 3 с движения? 5. Точка движется по прямой согласно уравнению х = At + Bt3, где А =6 м/с, В =0,125 м/с3. Определить среднюю скорость точки в интервале времени от t = 2 с до t = 6 с. 6. Тело брошено под углом α=300 к горизонту со скоростью υ = 30 м/с. Определить тангенциальное и нормаль- ное ускорения камня в конце первой секунды после начала движения. 7. Точка движется по окружности радиусом 2 м согласно уравнению S=At3, где А = 2 м/с3. В какой момент времени нормальное ускорение точки будет равно тангенциальному? Определить полное ускорение в этот момент. 8. Найти, во сколько раз нормальное ускорение точки, лежащей на ободе вращающегося колеса, больше ее тангенциального ускорения для того момента, когда вектор полного ускорения этой точки составляет угол 30° с вектором ее линейной скорости. 9. Радиус – вектор частицы изменяется со временем по закону 10. Две материальные точки движутся согласно уравнениям x1=A1 + В1t + C1t2 и x2 = A2 + C2t2, где А1 =10 м, В1 = 32 м/с, С1 = – 3 м/с2, А2 = 5 м, С2 = 5 м/с2. В какой момент времени скорости этих точек одинаковы? Чему равны скорости и ускорения точек в этот момент? 11. Якорь электромотора, вращающийся с частотой n = 50 об/с, двигаясь после выключения тока равнозамедленно, остановился, сделав N = 1680 об. Найти угловое ускорение якоря.
12. Ротор электродвигателя, имеющий частоту враще- ния n = 955 об/мин, после выключения остановился через t = 10 с. Считая вращение равнозамедленным, определить угловое ускорение ротора после выключения электро- двигателя. Сколько оборотов сделал ротор до остановки? 13. Колесо радиусом R = 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением j = А + Вt + Ct3, где В =2 рад/с, С=1 рад/с3. Для точек, лежащих на ободе колеса, найти через время t = 2 с после начала движения следующие величины: а) угловую скорость, б) линейную скорость, в) угловое ускорение, г) тангенциальное ускорение, д) нормальное ускорение. 14. Колесо вращается вокруг неподвижной оси так, что угол его поворота изменяется со временем по закону j = Вt2, где В = 0,20 рад/с2. Найти полное ускорение точки на ободе колеса в момент t = 2,5 с, если линейная скорость точки в этот момент υ = 0,65 м/с. 15. Твердое тело вращается вокруг неподвижной оси по закону j = Аt – Вt3, где А = 6,0 рад/с, В = 2,0 рад/с3. Найти средние значения угловой скорости и углового ускорения за промежуток времени от начала движения до остановки. Определить угловое ускорение в момент остановки тела. 16. Маховик, вращающийся с постоянной частотой n1 =10 об/с, начал вращаться равнозамедленно. Когда торможение прекратилось, вращение снова было равномерным с частотой n2 =6 об/с. Определить угловое ускорение маховика и продолжительность торможения, если за время равнозамедленного движения маховик сделал N = 50 об. 17. Диск радиусом 10 см, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением e = 0,5 рад/с2. Найти тангенциальное, нормальное и полное ускорение точек на окружности диска в конце второй секунды после начала вращения. 18. Колесо радиусом R = 0,3 м вращается согласно уравнению j = Аt+ Вt3, где А = 1 рад/с, В = 0,1 рад/с3. Определить полное ускорение точек на окружности колеса в момент времени t =2 с. 19. Диск вращается с угловым ускорением e = ‑ 2 рад/с2. Сколько оборотов N сделает диск при изменении частоты вращения от n1 = 240 мин–1 до n2 = 90 мин–1? Найти время Dt, в течение которого это произойдет. 20. Маховик начал вращаться из состояния покоя равноускоренно и, сделав 40 полных оборотов, приобрёл угловую скорость 10 21. Тело массой m =1кг движется так, что пройденное расстояние от времени дается уравнением 22. Тело массой m =1 кг движется так, что его коорди- наты х и у изменяются от времени следующим образом:
23. Определить ускорение грузов массы
24. За какое время тело соскользнёт с наклонной плоскости высотой h = 0,9 м и углом наклона β = 600, если по наклонной плоскости с углом наклона α= 300 оно движется вниз равномерно?
25. В установке, показанной на рисунке, массы тел равны m 1, m 2 и m 3, масса блока пренебрежимо мала и трения в блоке нет. Найти ускорение, с которым опускается тело m 3, и силу натяжения нити, связывающей тела m 1 и m 2, если коэффициент трения между этими телами и горизонтальной поверхностью равен k.
Массой блока пренебречь.
32. На горизонтальной поверхности лежат два бруска массами m1 = 100 г и m2 = 200 г. Между ними вставлена лёгкая пружина, сжатая нитью на величину Δ l = 1 см. В некоторый момент нить пережигают, и бруски разъезжаются в разные стороны. Меньший брусок останавливается, пройдя путь L =34 см. Определите жёсткость пружины, если коэф- фициент трения брусков о плоскость равен 0,1.
33. Мяч, летящий со скоростью υ 0 = 15 м/с, отбрасывается ракеткой в противоположную сторону со скоростью υ 1= 20 м/с. Найти изменение импульса, если изменение кинетической энергии ΔW = 8,75 Дж. 34. Два шара массой m 1 = 9 кг и m 2 = 12 кг подвешены на нитях длиной l = 1,5 м. Первоначально шары соприкасаются между собой, затем меньший шар отклонили на угол α = 30º и отпустили. Считая удар неупругим, определить высоту h, на которую поднимутся оба шара после удара. 35. Два шара подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Масса первого шара 0,2 кг, масса второго – 0,1 кг. Первый шар отклоняют так, что его центр тяжести поднимается на высоту 4,5 см, и отпускают. На какую высоту поднимутся шары после соударения, если: а) удар упругий, б) удар неупругий? 36. Шар массой m 1 = 6 кг движется со скоростью υ1 =2 м/с и сталкивается с шаром массой m 2 = 4 кг, который движется ему навстречу со скоростью υ 2 = 5 м/с. Найти скорость шаров после прямого центрального удара. Удар считать абсолютно упругим. 37. Шар массой m 1 = 5 кг движется со скоростью υ1 =2 м/с и сталкивается с покоящимся шаром массой m 2 =3 кг. Вычислить работу, совершенную при деформации шаров при прямом центральном ударе. 38. На покоящийся шар налетает со скоростью υ = 4 м/с другой шар одинаковой с ним массы. В результате столкнове- ния шар изменил направление движения на угол 30°. Опреде- лить скорости шаров после удара. Удар считать упругим. 39. На железнодорожной платформе, движущейся по инерции со скоростью υ 0 = 3 км/ч, укреплено орудие. Масса платформы с орудием М = 10 т. Ствол орудия направлен в сторону движения платформы. Снаряд массой m = 10 кг вылетает из ствола под углом α = 60º к горизонту. Определить скорость снаряда (относительно Земли), если после выстрела скорость платформы уменьшилась в n = 2 раза. 40. Частица массы m 1 налетела со скоростью υ на неподвижную частицу массы m 2, которая после упругого удара полетела под углом α к первоначальному направлению движения налетающей частицы. Определите скорость частицы m 2 после удара. 41. Подсчитать работу поднятия груза массой m = =200 кг по наклонной плоскости длиной l = 5 м, составляющей с горизонтом угол α = 30º, если ускорение тела при подъёме равно а = 0,5 м/с2, коэффициент трения μ = 0,1. 42. Вагон массой m = 20 т, двигаясь равнозамедленно с начальной скоростью υ0 = 54 км/ч, останавливается через некоторое время под действием силы трения, которая изменяется с расстоянием по закону F = – ax, где a = 100 Н/м. Найти работу силы трения и расстояние, которое пройдёт вагон до остановки. 43. На какую глубину погрузится тело, падая с высоты h в воду, если плотность тела ρ меньше плотности воды ρ 1? Трением тела о воздух и воду пренебречь. 44. Сила, действующая на частицу, имеет вид 45. Тело массой m начинает двигаться под действием силы 46. Спортсмен с высоты h = 12 м падает на упругую сетку. Пренебрегая массой сетки, определить, во сколько раз наибольшая сила давления спортсмена на сетку больше его силы тяжести, если прогиб сетки, под действием только силы тяжести спортсмена х0 = 15 см. 47. Пуля массой m = 15 г, летящая горизонтально, падает в баллистический маятник длиной l = 1 м и массой М = 1,5 кг и застревает в нём. Маятник в результате этого отклонился на угол φ = 30º. Определить скорость пули. 48. Потенциальная энергия частицы имеет вид U = d/r, где r – модуль радиус-вектора частицы, d = const. Найти силу 49. Конькобежец, стоя на льду, бросил вперёд гирю массой m 1=5 кг и вследствие отдачи покатился назад со скоростью υ 2=1 м / с. Масса конькобежца m 2 = 60 кг. Определить работу А, совершённую конькобежцем при бросании гири. 50. На барабан, представляющий однородный цилиндр радиусом R = 0,2 м и массой m 1 = 9 кг, намотан шнур, к концу которого привязан груз массой m 2 = 2 кг. Найти ускорение груза и кинетическую энергию системы спустя время t =3 с. 51. На горизонтальную ось насажены маховик и лёгкий шкив радиусом R =5 см. На шкив намотан шнур, к которому привязан груз массой m =0,4 кг. Опускаясь равноускоренно, груз прошел путь S =1,8 м за время t = 3 c. Определить момент инерции I маховика. Массу шкива считать пренебрежимо малой. 52. В установке, показанной на рисунке, известны масса однородного сплошного цилиндра m, его радиус R и массы тел m1 и m2. Найти угловое ускорение цилиндра и отношение натяжений Т2/Т1 вертикальных участков нити в процессе движения.
53. В системе, показанной на рисунке, известны массы тел m 1 и m 2, коэффициент трения k между телом m 1 и горизонтальной плоскостью, а также масса блока m, который можно считать однородным диском. Найти ускорение тела m 2 и работу силы трения, действующей на тело m 1, за первые t секунд после начала движения.
56. Вал массой m =100 кг и радиусом R = 5 см вращается с частотой n = 8 с- 1. К цилиндрической поверхности вала прижали тормозную колодку с силой F = 40 Н, под действием которой вал остановился через t =10 с. Определить коэф- фициент трения μ. 57. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязаны грузики массой m1 =100 г и m2 =110 г. С каким ускорением a будут двигаться грузики, если масса блока m равна 400 г. Трение при вращении ничтожно мало. 58. На барабан радиусом R = 20 см, момент инерции которого J = 0,1 кг∙м2, намотан шнур, к концу которого привя- зан груз массой m = 0,5 кг. До начала вращения барабана груз находился на высоте h = 1 м над полом. Через какое время груз опустится на пол и какова будет при этом кинетическая энергия системы?
60. На барабан радиусом R = 20 см, момент инерции которого J = 0,1 кг∙м2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана груз находился на высоте h = 1 м над полом. Через какое время груз опустится на пол и какова будет при этом кинетическая энергия системы? 61. Маховик в виде сплошного диска, момент инерции которого J = 1,5 кг∙м2, вращаясь равнозамедленно, за время t = 1 мин уменьшил частоту своего вращения с n 0 = 240 об/мин до n 1 = 120 об/мин. Определить: 1) угловое ускорение маховика; 2) момент силы торможения; 3) работу торможения. 62. На скамье Жуковского сидит человек и держит в вытянутых руках гири по 10 кг каждая. Расстояние от каждой гири до оси вращения скамьи l1=50 см. Скамья вращается с частотой n 1=1 с–1. Как изменится частота вращения скамьи и какую работу произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l2=20 см? Суммарный момент инерции человека и скамьи относительно оси вращения J = 2,5 кг м2.
63. На краю свободно вращающегося достаточно большого горизонтального диска, имеющего радиус R и момент инерции J, стоит человек массой m. Диск совершает n1 об/мин. Как изменится скорость вращения диска, если человек перейдет от края диска к центру? Какую работу совершит человек при переходе? Размерами человека по сравнению с радиусом диска можно пренебречь. 64. Шарик массой m =50 г, привязанный к концу нити длиной l1=1 м, вращается с частотой n 1=1 об/с, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси вращения до расстояния l2=0,5 м. С какой часто- той будет при этом вращаться шарик? Какую работу совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь. 65. На краю горизонтальной платформы, имеющей форму диска радиусом R = 2 м, стоит человек. Масса платформы M = 240 кг, масса человека m = 80 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль ее края со скоростью υ = 2 м/с относительно платформы. 66. Человек стоит на скамье Жуковского и держит в руках стержень, расположенный вертикально вдоль оси вращения скамейки; стержень служит осью вращения колеса, расположенного на верхнем конце стержня. Скамья непод- вижна, колесо вращается с частотой n 1=10 с–1. Радиус колеса равен 20 см, его масса m =3 кг. Определить частоту вращения n 2 скамьи, если человек повернет стержень на угол 180°? Суммарный момент инерции человека и скамьи равен 6 кг×м2. 67. Вертикально расположенный однородный стержень массы M и длины l может вращаться вокруг своего верхнего конца. В нижний конец стержня попала, застряв, горизонталь- но летевшая пуля массы m, в результате чего стержень отклонился на угол a. Считая m << M, найти скорость летевшей пули. 68. Два горизонтально расположенных диска свободно вращаются вокруг вертикальной оси, проходящей через их центры. Моменты инерции дисков относительно этой оси равны J1 и J2, а угловые скорости w1 и w2. После падения верхнего диска на нижний оба диска благодаря трению между их поверхностями начинают вращаться как единое целое. Найти установившуюся угловую скорость дисков и приращение кинетической энергии вращения этой системы. 69. Стержень длиной l=1.5 м и массой M =10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня. В середину стержня попадает пуля массой m =10 г, летящая в горизонтальном направлении со скоростью υ = 500 м/с, и застревает в стержне. На какой угол отклонится стержень после удара? 70. Бревно высоты h = 3 м и массы m = 50 кг начинает падать из вертикального положения на землю. Определить скорость верхнего конца и момент импульса бревна в момент падения на землю. 71. Плотность смеси азота и водорода при температуре t = 47 °С и давлении P = 2.105 Па равна r = 0,3 г/л. Найти концентрации молекул азота (n1) и водорода (n2) в смеси. 72. В баллоне емкостью 2 дм3 содержится смесь азота N2 и окиси азота NO. Определить массу окиси азота, если масса смеси равна 14 г, температура 300 К и давление 0,6×106 Па. 73. Найти плотность газовой смеси, состоящей по массе из одной части водорода и восьми частей кислорода при давлении Р = 100 кПа и температуре Т = 300 К. 74. В баллоне, объём которого 0,25 м 3, находится газ, состоящий из смеси СО2 и паров воды. Температура газа 327° С. Число молекул углекислого газа N 1 = 6,6.1021. Найти давление и молярную массу газовой смеси. 75. Определить давление и молекулярную массу смеси газов, состоящей из 10 г кислорода и 10 г азота, которые занимают объём 20 л при температуре 150° С. 76. Какому давлению необходимо подвергнуть углекислый газ при температуре Т = 300 К, чтобы его плотность оказалась равной r = 500 г/л? 77. На какой высоте h плотность кислорода уменьшается на 1 %? Температура кислорода 27 ° С. 78. На сколько уменьшится атмосферное давление Р = 100 кПа при подъёме наблюдателя над поверхностью Земли на высоту h = 200 м? Считать, что температура воздуха Т = 290 К и не изменяется с высотой. 79. Масса m каждой из пылинок, взвешенных в воздухе, равна 1 г. Отношение концентрации n1 пылинок на высоте h1 =1 м к концентрации n0 их на высоте h0 = 0 равна 0,787. Температура воздуха Т = 300 К. Найти по этим данным значение постоянной Авогадро. 80. Установленная вертикально закрытая с обоих концов труба наполнена кислородом. Высота трубы h = 200 м, объем V = 200 л. Стенки трубы имеют всюду одинаковую температуру Т = 293 К. Давление газа внутри трубы, вблизи ее основания равно Р0 = 105 Па. Определить количество молекул кислорода, содержащихся в трубе. 81. Вычислить наиболее вероятную, среднюю и среднюю квадратичную скорости молекул газа, плотность которого при нормальном атмосферном давлении r =1,0 г/л. 82. Найти относительное число молекул газа, скорости которых отличаются не более, чем на ∆h =1% от наиболее вероятной скорости. 83. Какая часть молекул кислорода при 0 ° С обладает скоростью от 100 м/с до 110 м/с? 84. Найти относительное число молекул газа, скорости которых отличаются не более, чем на ∆h = 1,5% от средней квадратичной скорости. 85. Какая часть молекул газа имеет скорости, превышающие наиболее вероятную скорость? 86. Азот находится при нормальных условиях. Найти: а) число столкновений, испытываемых в среднем каждой молекулой за одну секунду; б) число всех столкновений, происходящих между молекулами в 1 см3 азота, ежесекундно. Эффективный диаметр молекул принять равным 3,75×10-10 м . 87. Найти число столкновений, которые происходят в течение секунды между всеми молекулами, находящимися в объёме V = 1,0 мм3 водорода при нормальных условиях. Принять для водорода d =2,3 .10-10 м. 88. Какова плотность разреженного водорода, если средняя длина свободного пробега молекул равна 1 см? 89. При каком давлении средняя длина свободного пробега молекул равна 2.5 см, если его температура 68° С? 90. Найти среднюю длину свободного пробега и частоту столкновений молекул при нормальных условиях. Эффективный диаметр молекулы воздуха d = 3.10-10 м, масса одного моля М = 29 г/моль. 91. Газообразный водород, находившийся при нормаль- ных условиях в закрытом сосуде объемом V = 5,0 л, охладили на DТ = 55 К. Найти приращение внутренней энергии газа и количество отданного им тепла. 92. Идеальный газ с g = 1,4 расширяется изотермически от объема V 1 = 0,1 м3 до объема V 2 = 0,3 м3. Конечное давление газа P 2 = 2,0×105 П а. Определить приращение внутренней энергии газа, совершенную газом работу и количество полученного газом тепла. 93 При изобарном нагревании от 0 до 100 ° С моль идеального газа поглощает Q = 3,35 кДж тепла. Определить: 1) значение g; 2) приращение внутренней энергии газа DU; 3) работу, совершенную газом. 94. При адиабатном сжатии кислорода массой m = 20 г его внутренняя энергия увеличилась на DU = 8 кДж и температура повысилась до Т2 = 900 К. Найти: 1) повышение температуры DТ; 2) конечное давление газа Р 2, если начальное давление Р 1 = 200 кПа. 95. Какое количество теплоты выделяется при изотер- мическом сжатии 10 л газа, находившегося под давлением 1,5.105 Па, до объёма 2 л? 96. Чему равны удельные теплоемкости Сv и Cp некоторого двухатомного газа, если плотность этого газа при нормальных условиях равна r 0 = 1,43 кг×м3? Какой это газ? 97. Определить удельные теплоёмкости Cр и Cv для газа, состоящего по массе из 85 % О2 и 15 % озона (О3). 98. 25 % молекул кислорода диссоциировано на атомы. Определить удельные теплоемкости Сv и Cp такого газа. 99. Азот занимает объём V 1=2 м3 и находится под давлением P 1 = 105 Па. Газ нагревают сначала при постоянном объёме до давления P 2 = 5.105 Па, а затем при постоянном давлении до объёма V 2 = 4 м3. Масса азота m = 3 кг. Определить изменение внутренней энергии газа, совершенную работу и количество тепла, переданное газу. 100. Воздух, занимавший объём V 1= 10 л при давлении P 1 = 100 кПа, был адиабатно сжат до объёма V 2 = 1 л. Под каким давлением P 2 находится воздух после сжатия? 101. Идеальный двухатомный газ в количестве ν =1 моль совершает цикл, состоящий из двух изохор и двух изобар. Наименьший объём газа 10 л, наибольший – 20 л, наименьшее давление 2,46.105 Па, наибольшее – 4,1.105 П а. Начертить график цикла. Определить температуры газа для характерных точек цикла и его КПД. 102. Один моль идеального двухатомного газа, находя- щийся под давлением P 1 = 0,1 МПа при температуре Т 1 = 300 К, нагревают при постоянном объеме до давления P 2 = 0,2 МПа. После этого газ изотермически расширяется до начального давления и затем изобарически сжимается до начального объема. Начертить график цикла. Определить температуру газа для характерных точек цикла и его КПД. 103. Идеальный газ совершает цикл Карно. Темпера- тура Т 1 нагревателя равна 470 К, температура Т 2 холодильника – 270 К. При изотермическом расширении газ совершает работу А = 100 Дж. Определить КПД цикла и количество теплоты Q 2, которое газ отдаёт охладителю при изотерми- ческом сжатии. 104. Идеальный газ совершает цикл Карно. Работа А 1 изотермического расширения газа равна 5 Дж. Определить работу А 2 изотермического сжатия, если КПД цикла 0,2. 105. Идеальный газ, совершающий цикл Карно, 2/3 количества теплоты Q1, полученного от нагревателя, отдаёт холодильнику. Температура холодильника 275 К. Определить температуру нагревателя. 106. Найти изменение энтропии при следующих процессах: а) при превращении 1 кг воды при 0 ° С в пар при 100 ° С; б) при превращении 30 г льда в пар при 100 °С, если начальная температура льда - 40 ° С. 107. Найти приращение энтропии одного моля углекис- лого газа при увеличении его абсолютной температуры в n = 2 раза, если процесс нагревания: а) изохорный; б) изобарный. 108. Гелий массой m = 1,7 г адиабатически расширили в n = 3 раза и затем изобарически сжали до первоначального объема. Найти приращение энтропии газа в этом процессе. 109. Смешали воду массой m = 2 кг при температуре Т1 =280 К с водой массой m2 =10 кг при температуре Т2 =350 К. Найти 1) температуру смеси; 2) изменение энтропии, происходящее при смешивании. 110. Кислород массой m = 2 кг. Увеличил свой объём в N =5 раз один раз адиабатически, другой изотермически. Найти изменения энтропии в каждом из двух процессов. 111. Четыре одинаковых точечных заряда q = 10 нКл расположены в вершинах квадрата со стороной a = 10 см. Найти силу, действующую со стороны трех зарядов на четвертый. 112. Четыре одинаковых по модулю точечных заряда |q | =20 нКл, два из которых положительны, а два отрица- тельны, расположены в вершинах квадрата со стороной a = 20 см. Найти силу, действующую на помещенный в центр квадрата положительный точечный заряд Q =20 нКл. 113. Три одинаковых точечных заряда q =20.10-9 Кл расположены в вершинах равностороннего треугольника. На каждый заряд действует сила F =10 мН. Найти длину a стороны треугольника. 114. Три одинаковых точечных заряда q = 9 нКл распо- ложены в вершинах равностороннего треугольника. Какой точечный заряд q0 нужно поместить в центре треугольника, чтобы система находилась в равновесии? 115. Два положительных точечных заряда находятся на расстоянии 0,5 м один от другого. Один заряд вдвое больше другого. На прямой, их соединяющей, находится в равновесии заряженный шарик. Найти расстояние от этого шарика до большего заряда. Будет ли равновесие устойчивым? 116. Заряды q1 = 40 нКл и q2 = -10 нКл расположены на расстоянии r =10 см друг от друга. Какой надо взять третий заряд и где следует его поместить, чтобы система находилась в равновесии? 117. Два шарика массой m =0,1 г каждый подвешены в одной точке на нитях длиной l =20 см каждая. Получив одина- ковые заряды, шарики разошлись так, что нити образовали между собой угол 2 a = 60о. Найти заряд каждого шарика. 118. Два одинаковых заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол a. Шарики погружаются в масло с плотностью rо = 8.102 кг/м3. Определить диэлектрическую проницаемость e масла, если угол расхождения нитей при погружении шариков в масло останется неизменным. Плотность материала шариков r =1,6.103 кг/м3. 119. Два одинаковых шарика подвешены в воздухе на нитях так, что их поверхности соприкасаются. После того, как каждому шарику был сообщен заряд q =0,4 мкКл, шарики разошлись на угол 2a = 60о. Найти массу шариков, если расстояние от центров шариков до точки подвеса l =0,2 м. 120. Маленький шарик массой m =0,01 мг, несущий заряд q =10 нКл, помещен в однородное электрическое поле, направленное горизонтально. Шарик приходит в движение без начальной скорости и через время t = 4 с приобретает скорость u =50 м/с. Найти напряженность поля. 121. Расстояние d между точечными положительными зарядами q1 = 9 q и q2 = q равно 8 см. На каком расстоянии r от первого заряда находится точка, в которой напряженность Е поля зарядов равна нулю? Где находилась бы эта точка, если бы второй заряд был отрицательным? 122. Электрическое поле создано двумя точечными зарядами q1 =40 нКл и q2 = -10 нКл, находящимися на расстоя- нии d =10 см друг от друга. Определить напряженность Е в точке, удаленной от первого заряда на r1 = 12 см и от второго на r2 = 6 см. 123. В вершинах квадрата со стороной a = 5 см нахо- дятся одинаковые положительные заряды q = 2 нКл. Опреде- лить напряженность поля в середине одной из сторон квадрата. 124. Электростатическое поле создано двумя бесконеч- ными параллельными плоскостями, заряженными с поверхно- стной плотностью s1 =1 нКл/м2 и s2 = -2 нКл/м2. Определить напряженность электростатического поля: 1) между плоскостями; 2) за пределами плоскостей. Построить график Е(x). 125. Одинаковые по модулю, но разные по знаку заряды | q |=18 нКл расположены в вершинах равностороннего треуголь- ника со стороной a = 2 м. Найти напряженность поля Е в третьей вершине треугольника. 126. Две бесконечные параллельные плоскости находят ся на расстоянии d =1 см друг от друга. На плоскостях равномерно распределены заряды с поверхностными плотностями s1 = 0,2 мкКл/м2 и s2 = -0,3 мкКл/м2. Определить разность потенциалов между плоскостями. 127. В двух вершинах равностороннего треугольника помещены одинаковые заряды q1 = q2 = q = 5 мкКл. Какой точечный заряд необходимо поместить в середину стороны, соединяющей заряды q1 и q2, чтобы напряженность электриче- ского поля в третьей вершине треугольника оказалась равной нулю? 128. Электрическое поле создано двумя бесконечными параллельными пластинами, несущими одинаковый равномерно распределенный по площади заряд (s =1 нКл/м2). Определить напряженность Е поля: 1) между пластинами; 2) вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам. 129. Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распреде -ленный по площади заряд с поверхностными плотностями s1 =1 нКл/м2 и s2 =3 нКл/м2. Определит
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 632; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.79.165 (0.015 с.) |

 . Найти: а) векторы скорости и ускорения; б) модуль скорости в момент t = 1 c.
. Найти: а) векторы скорости и ускорения; б) модуль скорости в момент t = 1 c. . Определить угловое ускорение маховика и продолжительность равноускоренного вращения.
. Определить угловое ускорение маховика и продолжительность равноускоренного вращения. , где а =5см,
, где а =5см,  . Найти ускорение, силу и импульс тела через
. Найти ускорение, силу и импульс тела через  с после начала движения.
с после начала движения. ,
,  , где
, где 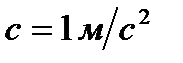 ,
, 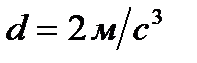 . Опреде- лить ускорение и действующую на тело силу к концу пятой секунды.
. Опреде- лить ускорение и действующую на тело силу к концу пятой секунды.
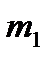 ,
,  ,
,  в системе. Массой блоков пренебречь. Трение отсутствует.
в системе. Массой блоков пренебречь. Трение отсутствует.
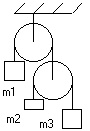 29. Определить ускорение грузов массы
29. Определить ускорение грузов массы  и
и  , а также силу натяжения нитей в системе блоков, если
, а также силу натяжения нитей в системе блоков, если  . Массой блоков пренебречь. Трение отсутствует.
. Массой блоков пренебречь. Трение отсутствует.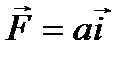 , где а – константа. Вычислить работу, совершаемую над частицей этой силой на пути от точки с координатами (1,2,3) м до точки с координатами (7,8,9) м.
, где а – константа. Вычислить работу, совершаемую над частицей этой силой на пути от точки с координатами (1,2,3) м до точки с координатами (7,8,9) м. . Найти мощность, развиваемую силой в момент времени t.
. Найти мощность, развиваемую силой в момент времени t. , действующую на частицу, работу, совершаемую этой силой над частицей при её переходе из точки М (1,2,3) в точку N (2,3,4).
, действующую на частицу, работу, совершаемую этой силой над частицей при её переходе из точки М (1,2,3) в точку N (2,3,4).


