
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение вращательного движенияСодержание книги Поиск на нашем сайте
ТВЕРДОГО ТЕЛА
Цель работы: изучить основной закон динамики вращательного движения твердого тела, экспериментально определить момент инерции крестообразного маховика и установить зависимость момента инерции маховика от распределения его массы относительно оси вращения. Приборы и принадлежности: экспериментальная установка, секундомеры, штангенциркуль, набор гирь, линейка. Краткая теория.
Определим величину работы
Произведение вращающей силы F на радиус r есть момент вращающей силы, действующий на данное тело, и обозначается через М (напомним, что моментом данной силы относительно какой-нибудь оси называется произведение этой силы на ее плечо, т.е. на длину перпендикуляра, проведенного от указанной оси до направления действия силы). Таким образом, в формуле (1)
Если вращающий момент (сила F или ее плечо r) с течением времени изменяется, то совершаемая работа определяется как сумма:
Момент вращающей силы представляется в виде вектора, совпадающего с осью вращения; положительную ориентировку этого вектора выбирают в том направлении, в котором перемещался бы правый винт, вращаемый этим моментом. Вращающий момент М, приложенный к телу, сообщает ему некоторое угловое ускорение e; согласно выбранным нами направлениям векторов Работа движущей силы равна изменению кинетической энергии тела, к которому эта сила приложена:
где w – угловая скорость. Здесь предполагается, что момент инерции тела J при вращении не изменяется. Разделив уравнение (4) на dt и сократив на
Формула (5) выражает основной закон динамики вращательного движения твердых тел, для которых J = const. Момент инерции точки относительно оси вращения равен произведению массы точки на квадрат расстояния от оси вращения до данной точки. В основном законе динамики вращательного движения твердого тела J – момент инерции тела относительно оси вращения. Момент инерции тела есть величина, характеризующая инертность тела при вращении. В уравнениях вращательного движения роль момента инерции аналогична роли массы в уравнениях поступательного движения. Момент инерции тела относительно некоторой оси равен сумме моментов инерции всех элементов (точек) тела относительно этой оси и выражается формулой:
где r – плотность тела, Любое тело независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от состояния своего движения. Измеряется момент инерции в
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.116.34 (0.008 с.) |



 Предположим, твердое тело А может вращаться вокруг некоторой неподвижной оси. Для того чтобы вызвать вращение тела (изменить его угловую скорость), необходимо внешнее воздействие. Однако сила
Предположим, твердое тело А может вращаться вокруг некоторой неподвижной оси. Для того чтобы вызвать вращение тела (изменить его угловую скорость), необходимо внешнее воздействие. Однако сила  , направление которой проходит через ось вращения, или
, направление которой проходит через ось вращения, или  , параллельная оси вращения, не могут изменить угловую скорость тела. Поэтому из приложенной к телу внешней силы R необходимо выделить составляющие
, параллельная оси вращения, не могут изменить угловую скорость тела. Поэтому из приложенной к телу внешней силы R необходимо выделить составляющие  Заметим, что при вращении тела составляющие
Заметим, что при вращении тела составляющие  , которую совершает вращающая сила, если точка приложения ее смещается по окружности радиуса r на
, которую совершает вращающая сила, если точка приложения ее смещается по окружности радиуса r на  . Предположим, что величина силы F при этом остается постоянной. Тогда
. Предположим, что величина силы F при этом остается постоянной. Тогда (1)
(1) , следовательно, работа, совершаемая вращающим моментом, равна произведению этого момента на угол поворота тела:
, следовательно, работа, совершаемая вращающим моментом, равна произведению этого момента на угол поворота тела: (2)
(2) ;
;  . (3)
. (3) и
и  , они ориентированы по оси вращения в одну и ту же сторону. Связь между величиной вращающего момента и величиной сообщаемого им углового ускорения можно получить следующим образом.
, они ориентированы по оси вращения в одну и ту же сторону. Связь между величиной вращающего момента и величиной сообщаемого им углового ускорения можно получить следующим образом. . Тогда для вращающегося тела, согласно формуле
. Тогда для вращающегося тела, согласно формуле  , имеем:
, имеем: (4)
(4) получаем:
получаем: . (5)
. (5) , (6)
, (6) расстояние от элемента массы до оси вращения, V – объем тела. Интегрирование производится по всему объему тела. Таким образом, момент инерции зависит не только от массы тела, но и от ее распределения относительно оси вращения.
расстояние от элемента массы до оси вращения, V – объем тела. Интегрирование производится по всему объему тела. Таким образом, момент инерции зависит не только от массы тела, но и от ее распределения относительно оси вращения.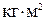 .
.


