
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение момента инерции шаров малого радиусаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: экспериментальным путём определить моменты инерции шара, выяснить физический смысл этой величины. Приборы и принадлежности: штатив, два желоба, шары малых радиусов, линейка, штангенциркуль. Краткая теория При изучении вращения твёрдых тел пользуются понятием момента инерции. Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс материальных точек системы на квадраты их расстояний до рассматриваемой оси: J = В случае непрерывного распределения масс эта сумма сводится к интегралу: J= где интегрирование производится по всему объёму тела. Величина r в этом случае есть функция положения точки с координатами x, y, z.
 В качестве примера найдём момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси. Разобьём цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r + dr. Момент инерции каждого полого цилиндра dJ = r2dm (так как dr << r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm – масса всего элементарного цилиндра; его объем В качестве примера найдём момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси. Разобьём цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r + dr. Момент инерции каждого полого цилиндра dJ = r2dm (так как dr << r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm – масса всего элементарного цилиндра; его объем  . Если . Если  – плотность материала, то dm = 2 – плотность материала, то dm = 2  и dJ = 2 и dJ = 2  . .
Тогда момент инерции сплошного цилиндра: J = Так как J = Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс Стела, сложенному с произведением массы m тела на квадрат расстояния а между осями: J = Jc + ma2; Значения моментов инерции для некоторых тел приводятся в таблице 1. Таблица 1
Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси Z, проходящей через него. Мысленно разобьем это тело на малые объёмы с элементарными массами m1, m2, …, mn, находящиеся на расстоянии r1, r2,…rn от оси. При вращении твёрдого тела вокруг неподвижной оси отдельные его элементарные объёмы массами mi опишут окружности различных радиусов ri с различными линейными скоростями vi. Но так как мы рассматриваем абсолютное твёрдое тело, то угловая скорость вращения этих объёмов одинакова:
Кинетическую энергию вращающегося тела найдём как сумму кинетических энергий его элементарных объёмов:
Используя выражение (1), получаем:
где Jz – момент инерции тела относительно оси Z. Таким образом, кинетическая энергия вращающегося тела:
Из сравнения формулы (2) с выражением для кинетической энергии тела, движущегося поступательно (Епост = mv2/2) следует, что момент инерции – мера инертности тела при вращательном движении. Формула (2) справедлива для тела, вращающегося вокруг неподвижной оси. В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:
где m – масса катящегося тела; vc – скорость центра масс тела; Jс – момент инерции тел относительно оси, проходящей через его центр масс;
На штативе закреплены два желоба АВ и А’B’C’ диаметром 1,9 см и толщиной 0,1см. Желоб А’В’С’ изогнут под углом Шар массой m, помещенный в точку А, обладает относительно горизонтального уровня BD запасом потенциальной энергии mgh. При его скатывании по желобу АВ потенциальная энергия преобразуется в кинетическую энергию поступательного движения mv2/2 (v – линейная скорость центра масс относительно желоба), кинетическую энергию вращательного движения J
При этом квадраты линейной и угловой скорости можно найти по формулам:
где Н – высота края желоба над поверхностью стола, l – дальность полёта шара до поверхности стола. Для вычисления работы трения Атр пускают тот же шар из точки А’ по желобу А’В’С’. Он, скатившись с высоты h по левой стороне желоба, поднимается на высоту h’< h по его правой половине. Подъём шара на высоту h’ определяют с помощью линейки. После проведения экспериментов шар извлекают через отверстие B’. Очевидно, изменение потенциальной энергии шара mg (h–h’) равно работе сил трения Атр, т.е. Атр = mg(h’– h). (6) Работа А1 совершается на пути длиной Аl = Умножив эту величину на А’B’ = h/sin
Подставляя выражения (5) и (8) в соотношение (4) и решая его относительно J, получим:
По этой формуле определяют момент инерции шара после измерений m, R, H, h, h’, l.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.241.205 (0.007 с.) |

 2.
2.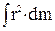 ,
, .
. – масса цилиндра, то момент инерции
– масса цилиндра, то момент инерции




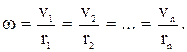 (1)
(1) или
или 

 . (2)
. (2) (3)
(3) – угловая скорость тела.
– угловая скорость тела.
 (радиус изгиба r = 2,5 см, расстояние А’В’ = 55 см, В’С’ = 45 см); желоб АВ идентичен части А’В’. В работе используются шары радиусами r = 0,25 – 0,35см.
(радиус изгиба r = 2,5 см, расстояние А’В’ = 55 см, В’С’ = 45 см); желоб АВ идентичен части А’В’. В работе используются шары радиусами r = 0,25 – 0,35см. /2 (
/2 ( . (4)
. (4) , (5)
, (5) , (где
, (где  – угол наклона желоба), следовательно, на единицу длины пути совершается работа сил трения, равная
– угол наклона желоба), следовательно, на единицу длины пути совершается работа сил трения, равная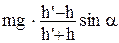 . (7)
. (7) . (8)
. (8) (9)
(9)


