
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Погрешности результатов измеренийСодержание книги Поиск на нашем сайте
Запрещается - переставлять на лабораторном столе приборы; - включать приборы в сеть без разрешения преподавателя; - касаться руками выводных клемм выпрямителя и клемм электромагнита.
При выполнении лабораторной работы № 4: запрещается находиться в плоскости вращения маховика.
При выполнении лабораторной работы № 5: - во избежание выхода из строя индикатора часового типа навешивать грузы рекомендуется плавно, без рывков; - грузы навешивать только на грузоприемную тарелку; - после выполнения работы снять грузы и грузоприемную платформу; запрещается держать руки под навешенными грузами.
При выполнении лабораторной работы № 6: - после выполнения работы остановить маятники; запрещается находиться в плоскости качания маятников.
При выполнении лабораторной работы № 7: - при приведении системы в колебательное движение не растягивать пружину до предела; - после выполнения работы снять грузы и пружины со штативов.
При выполнении лабораторной работы № 8: - после выполнения работы секундомер оставить включенным, микроскоп уложить в футляр; запрещается переставлять на столе сосуды с жидкостью. При выполнении лабораторной работы № 9: - проверить герметичность соединения шланга и резервуара с водой; запрещается: - касаться руками выходных клемм генератора; - наклонять установку.
При выполнении лабораторной работы № 10: запрещается: - касаться руками выводных клемм осциллографа и генераторов; - вставлять в разъемы и вынимать соединительные провода при включенных приборах.
При выполнении лабораторной работы № 11: - проверить надежность фиксации желобов в штативах. При выполнении лабораторной работы № 12: запрещается: - изменять наклон плоскости во время проведения опыта; - находиться в плоскости качаний маятника. Студенты НЕ ДОПУСКАЮТСЯ к выполнению лабораторных работ без предварительного инструктажа по технике безопасности. ЛАБОРАТОРНАЯ РАБОТА № 1
ИЗУЧЕНИЕ ЗАКОНОВ КИНЕМАТИКИ И ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
Цель работы: опытным путем проверить основные законы кинематики и динамики поступательного движения на машине Атвуда. Приборы и принадлежности: Машина Атвуда, электросекундомер СЭД-1М, грузы, перегрузки, выпрямитель ВС-24М.
Краткая теория. Кинематика Кинематикой называется раздел механики, в котором изучаются законы движения без учета причин этого движения. Различают два простейших вида движений твердого тела: поступательное движение и вращательное движение. Рассмотрим основные законы и формулы поступательного движения. При движении точки радиус-вектор, проведенный из начала координат в точку, и координаты точки, представляющие собой проекции радиус-вектора на соответствующие оси, изменяются и являются функциями времени:
Расстояние S, пройденное точкой также является функцией времени: S = S(t) (2) Равенства (1) и (2) называются кинематическими уравнениями движения точки. Если за время
Мгновенное ускорение определяется как предел отношения (3) при Одним из простейших видов механического движения является прямолинейное движение точки с постоянным ускорением. Для такого движения
При равномерном прямолинейном движении скорость точки с течением времени не изменяется: Динамика Динамика изучает движение тел с учетом причин, обусловливающих данное движение. При этом следует различать динамику поступательного движения и динамику вращательного движения. Рассмотрим основные законы и формулы динамики поступательного движения. Механическое движение тел изменяется в результате их взаимодействия. Количественной мерой такого взаимодействия является сила. Если на тело действуют несколько сил одновременно, то их действия можно заменить действием одной силы Основу динамики составляют три закона Ньютона.
Первый закон Ньютона. Существуют системы отсчета, относительно которых тело движется прямолинейно и равномерно или находится в покое, если равнодействующая всех сил, действующих на тело равна нулю. Такие системы отсчета называют инерциальными. При Второй закон Ньютона. Ускорение тела прямо пропорционально равнодействующей всех сил и обратно пропорционально массе тела: Третий закон Ньютона. Силы, с которыми тела действуют друг на друга, равны по величине и противоположны по направлению.
Основные законы кинематики и динамики могут быть проверены опытным путем на машине Атвуда. Описание экспериментальной Установки
Корпус (1) с сантиметровыми делениями, градуированная часть которого составляет 860 мм, имеет на обратной стороне паз с двумя токоведущими шинами, через которые с помощью приемного столика включается счетчик-секундомер. В нижней части корпуса имеются гнезда для подключения пускателя. Узел блока (2) состоит из блока диаметром 140 мм и кронштейна. По диаметру блока имеется проточка, по которой при проведении опыта с системой грузов перемещается нить. На боковой части блока проставлена его масса 109,9 г. Электромагнитный пускатель (3) служит для пуска и остановки грузов (4). Приемный столик (5) предназначен для разрыва цепи счетчика-секундомера и прекращения отсчета времени в момент удара грузом по чашке столика. Движущая система состоит из двух грузов (4), соединенных нитью, каждый из грузов состоит из двух цилиндров с полостями для засыпки дроби при тарировке. ЛАБОРАТОРНАЯ РАБОТА № 2 Краткая теория Тяжелое тело, свободно колеблющееся вокруг оси, не проходящей через центр тяжести, называется физическим маятником. Рассмотрим колебания абсолютно твердого тела в вертикальной плоскости относительно горизонтальной неподвижной оси. Так как ось вращения не проходит через центр тяжести, то момент силы тяжести относительно этой оси в отклоненном от равновесия состоянии, отличен от нуля. Если центр тяжести лежит в точке А на расстоянии l от оси вращения, то момент силы тяжести относительно оси:
где Момент силы направлен так, что тело движется к положению равновесия, в котором момент М становится равным нулю. Напишем уравнение моментов, полагая, что трение отсутствует:
где J – момент инерции маятника относительно оси качания. Ограничиваясь случаем малых отклонений
Обозначив
Как нетрудно убедиться простой подстановкой, решением уравнения (4) является функция:
Решением уравнения (4) является также функция
Колебания, происходящие со временем по закону синуса или косинуса, называются гармоническими. Так как Период колебаний физического маятника тем больше, чем больше его момент инерции и чем меньше расстояние от оси качания до его центра тяжести.
Сравнивая выражение для периода физического маятника с выражением для периода математического маятника Так как период колебаний физического маятника зависит от ускорения силы тяжести, то с его помощью можно определить величину g. Ньютон, впервые наблюдая качания маятников, изготовленных из различных материалов, установил, что ускорение силы тяжести в данной точки земной поверхности для всех тел одно и то же. Ускорение силы тяжести определяется особым оборотным маятником, в котором точка подвеса и центр качания обладают следующим свойством: при переносе точки подвеса физического маятника в центр качания прежняя точка подвеса становится новым центром качания.
ЛАБОРАТОРНАЯ РАБОТА № 3 ИЗУЧЕНИЕ СОУДАРЕНИй ШАРОВ
Цель работы: проверить закон сохранения импульса, вычислить коэффициент восстановления, определить энергию остаточной деформации при упругом и неупругом ударах. Приборы и принадлежности: Экспериментальная установка, шары разных диаметров, весы, масштабная линейка, выпрямитель ВС 4-12. Краткая теория
В механике под ударом следует понимать кратковременное взаимодействие двух или более тел, возникающее при их соприкосновении. Например, столкновение шаров, удар молотка о наковальню, попадание пули в мишень и т.д. Если в результате удара механическая энергия не изменяется, то удар называется абсолютно упругим. При ударе во время соприкосновения шаров происходит их деформация, точки соприкосновения переходят в круглые площадки. Кинетическая энергия ударяющегося тела переходит в энергию упругой деформации. При этом возникают упругие силы, возрастающие с увеличением деформации. Под действием этих сил шары начинают отталкиваться. Потенциальная энергия деформации переходит в кинетическую энергию движения, пока шары не разойдутся. Идеально упругому удару соответствует полное восстановление формы соударяющихся тел. Время соударения зависит от упругих констант материала тел, их относительной скорости в момент начала удара и их массы. Идеально упругих ударов не существует в природе, т.к. всегда часть энергии затрачивается на необратимую деформацию тел и увеличение их внутренней энергии. Но в отдельных случаях (например, когда шары стальные) потерями механической энергии можно пренебречь.
Если направление движения двух соударяющихся шаров в момент их соприкосновения совпадает с прямой, соединяющей центры шаров, то удар называется центральным. В данной работе рассматриваются центральные удары. Рассмотрим центральный абсолютно упругий удар двух шаров. Пусть шары массой
Записав эти равенства в виде
и разделив второе на первое, получим:
Таким образом, при центральном абсолютно упругом ударе шаров их относительная скорость меняет свое направление на противоположное, оставаясь неизменной по величине. В случае реального удара часть кинетической энергии шаров переходит при соударении в энергию остаточной деформации. Тогда
то есть относительная скорость шаров меняет свое направление и уменьшается по абсолютной величине. Для количественной оценки уменьшения относительной скорости вводится коэффициент восстановления К:
Величину коэффициента восстановления удобно определять при центральном ударе шаров одинаковой массы. Если оба шара отклонить на равные углы и одновременно освободить их, то они, сталкиваясь друг с другом, в любой момент времени будут иметь скорости, равные по величине, но разные по знаку. Коэффициент восстановления в этом случае равен
Уменьшение скорости после первого удара может оказаться небольшим, что приведет к большой погрешности при определении коэффициента восстановления. Поэтому целесообразно измерить скорость не после первого соударения, а после 10 – 15 соударений. Для n последовательных соударений может быть написано n уравнений:
Пренебрегая силами трения (при этом
Отношение скоростей может быть заменено отношением расстояний (дуг), проходимых шарами. Если шар опускается по вертикали на высоту h, то скорость v может быть представлена в виде:
где g – ускорение силы тяжести. Пусть l – длина подвеса шара, a – угол отклонения шара, S – расстояние, проходимое шаром. Тогда для малых углов отклонения
При
Уравнения (8) – (11) дают
где Формула (12) получена в предположении, что силы трения отсутствуют. В действительности имеет место сила трения шаров о воздух, что приводит к уменьшению амплитуды каждого последующего колебания даже при отсутствии соударений (т.е. при колебаниях одного шара). Закон амплитуды может быть представлен в виде
где В процессе колебаний с соударениями уменьшение амплитуды происходит не только в результате действия сил трения, но также и вследствие неполного восстановления скорости при соударениях. Так как амплитуда пропорциональна скорости в нижней точке, то
ЛАБОРАТОРНАЯ РАБОТА №4 ТВЕРДОГО ТЕЛА
Цель работы: изучить основной закон динамики вращательного движения твердого тела, экспериментально определить момент инерции крестообразного маховика и установить зависимость момента инерции маховика от распределения его массы относительно оси вращения. Приборы и принадлежности: экспериментальная установка, секундомеры, штангенциркуль, набор гирь, линейка. Краткая теория.
Определим величину работы
Произведение вращающей силы F на радиус r есть момент вращающей силы, действующий на данное тело, и обозначается через М (напомним, что моментом данной силы относительно какой-нибудь оси называется произведение этой силы на ее плечо, т.е. на длину перпендикуляра, проведенного от указанной оси до направления действия силы). Таким образом, в формуле (1)
Если вращающий момент (сила F или ее плечо r) с течением времени изменяется, то совершаемая работа определяется как сумма:
Момент вращающей силы представляется в виде вектора, совпадающего с осью вращения; положительную ориентировку этого вектора выбирают в том направлении, в котором перемещался бы правый винт, вращаемый этим моментом. Вращающий момент М, приложенный к телу, сообщает ему некоторое угловое ускорение e; согласно выбранным нами направлениям векторов Работа движущей силы равна изменению кинетической энергии тела, к которому эта сила приложена:
где w – угловая скорость. Здесь предполагается, что момент инерции тела J при вращении не изменяется. Разделив уравнение (4) на dt и сократив на
Формула (5) выражает основной закон динамики вращательного движения твердых тел, для которых J = const. Момент инерции точки относительно оси вращения равен произведению массы точки на квадрат расстояния от оси вращения до данной точки. В основном законе динамики вращательного движения твердого тела J – момент инерции тела относительно оси вращения. Момент инерции тела есть величина, характеризующая инертность тела при вращении. В уравнениях вращательного движения роль момента инерции аналогична роли массы в уравнениях поступательного движения. Момент инерции тела относительно некоторой оси равен сумме моментов инерции всех элементов (точек) тела относительно этой оси и выражается формулой:
где r – плотность тела, Любое тело независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от состояния своего движения. Измеряется момент инерции в ЛАБОРАТОРНАЯ РАБОТА № 5 Краткая теория Деформацией тела называется изменение его формы и размеров, обычно сопровождающееся и изменением объема тела. В некоторых случаях, например при деформации сдвига, изменение объема тела может и не наблюдаться. Деформации тела вызываются изменением температуры или воздействием на него внешних сил. В общих чертах, при деформации происходит смещение частиц, находящихся в узлах кристаллической решетки твердых тел, из первоначальных положений равновесия в новые. В результате в твердом теле возникают внутренние упругие силы. Если после прекращения действия сил деформация исчезает, то ее называют упругой. Неупругие деформации твердого тела сопровождаются необратимой перестройкой кристаллической решетки тела. В этом случае наблюдается остаточная или пластическая деформация тела. Упругие деформации имеют место тогда, когда внешние силы, вызывающие деформацию, не превосходят некоторого предела, называемого пределом упругости. При установившейся упругой деформации результирующая внутренняя упругая сила, возникающая в теле, в любом сечении тела уравновешивает внешние силы, действующие на тело. Поэтому при упругой деформации величина внутренних упругих сил может быть определена по величине внешних сил, приложенных к телу. Величину внутренних упругих сил характеризуют напряжением s, численно равным отношению результирующей упругой силы к площади поперечного сечения тела S:
Когда сила F направлена по нормали к поверхности S, напряжения называют нормальными. Если же сила направлена по касательной к этой поверхности, то напряжения называют касательными, или тангенциальными. Мерой деформации является относительная деформация e, равная отношению абсолютной деформации
Английский физик Р. Гук в 1675 г. опытным путем установил, что напряжения, возникающие в упруго деформированном теле, прямо пропорционально величине относительной деформации:
где Е – коэффициент пропорциональности для деформации сжатия и растяжения, называемый модулем Юнга. Соотношение (3) выражает закон Гука для любого вида упругих деформаций. Упругая деформация продольного растяжения, например проволоки, проявляется в изменении ее длины при изменении действующего на нее продольного натяжения. Для этого к проволоке должна быть приложена растягивающая сила, действие которой равномерно распределено по всему сечению. Относительную деформацию e в этом случае называют относительным удлинением При этом закон Гука примет вид:
Из соотношений (1) и (4) следует:
Модуль Юнга является постоянной величиной для данного вещества, поэтому его значение зависит только от материала, из которого изготовлено деформируемое тело. ЛАБОРАТОРНАЯ РАБОТА № 6 Краткая теория Среди множества различных незатухающих колебаний простейшим является гармоническое колебательное движение, описываемое функцией синуса или косинуса: Фаза колебания определяет значение колеблющейся величины в данный момент времени. Начальная фаза определяет значение х в начальный момент времени: для синусоидального колебания при t = 0 Простейший пример гармонического колебания – движение математического маятника.
Если точечное тело совершает гармоническое колебание, то согласно второму закону Ньютона на него должна действовать сила, равная
где Таким образом, чтобы тело совершало гармоническое колебательное движение, на него должна действовать сила, всегда направленная к положению равновесия, а по величине – прямо пропорциональная смещению от этого положения. Возвращающей силой, действующей на математический маятник, является проекция силы тяжести
где k – коэффициент пропорциональности между действующей на тело силой F и смещением х этого тела от положения равновесия. В этом случае колебания можно полагать гармоническими. Сравнивая выражение (2) с выражением (1), получим:
где l – длина маятника, g – ускорение силы тяжести. Если определить непосредственно Т, то можно измерить g. Однако при этом необходимо точно измерить l, что вызывает трудности. Чтобы обойти эти трудности, поступают следующим образом: измеряют периоды
Таким образом, достаточно измерить разность длин маятников, что проще, чем измерять длины
Возвращающим моментом является момент силы тяжести, имеющий знак, противоположный знаку угла отклонения a и равный
 (6) (6)
пропорционален углу отклонения и колебания маятника будут гармоническими. Выразим возвращающий момент как произведение углового ускорения на момент инерции колеблющегося тела:
Сравнив выражения (6) и (7), можно получить
Следовательно,
Таким образом, период малых колебаний физического маятника определяется по формуле (9), где J – момент инерции относительно оси качания, m-масса маятника, ЛАБОРАТОРНАЯ РАБОТА № 7 ПРУЖИННОГО МАЯТНИКА
Цель работы: измерить коэффициенты упругости и периоды собственных колебаний двух различных пружин и пружинных систем, полученных в результате их последовательного и параллельного соединения. Измерить величину логарифмического декремента затухания и рассчитать коэффициент сопротивления для пружинного маятника с воздушным демпфером. Приборы и принадлежности: экспериментальная установка, секундомер, набор пружин, набор грузов, воздушный демпфер. Краткая теория Колебания, происходящие при отсутствии переменных внешних сил, называются собственными; частота собственных колебаний зависит от свойств системы. Допустим, что в системе действуют только две силы:
где m – масса колеблющегося тела. Разделим это уравнение на массу тела и введем обозначения:
Получим дифференциальное уравнение:
Решением этого уравнения является функция:
где Таким образом, если на тело, кроме силы упругости действует сила трения, пропорциональная первой степени скорости, то тело будет совершать колебательное (не гармоническое!) движение с частотой, зависящей от m, k, b. Амплитуда колебаний (т.е. значение х при
называется коэффициентом затухания. Она определяет быстроту убывания амплитуды колебаний с течением времени. Произведение коэффициента затухания на период колебаний Т
равное логарифму отношения двух соседних амплитуд
есть безразмерная величина, которая называется логарифмическим декрементом затухания. Он пропорционален величине коэффициента сопротивления, периоду и обратно пропорционален массе системы. Пружинный маятник – это система, состоящая из груза массой m, подвешенного на пружине, массой которой можно пренебречь. В состоянии равновесия сила тяжести груза уравновешивается равной по величине, но противоположно направленной силой упругости пружины
где | |||||||||
|
| Поделиться: |

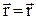 (t);
(t);  (t);
(t); 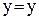 (t). (1)
(t). (1)
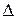 t точка переместится на расстояние
t точка переместится на расстояние 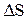 , то ее средняя скорость перемещения за это время
, то ее средняя скорость перемещения за это время 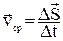 . Скорость в данный момент времени – мгновенную скорость – можно определить как предел этого отношения при условии, что
. Скорость в данный момент времени – мгновенную скорость – можно определить как предел этого отношения при условии, что 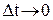 :
: 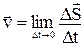 . Если за время
. Если за время  мгновенная скорость изменилась от
мгновенная скорость изменилась от 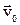 до
до  , то среднее ускорение точки за это время
, то среднее ускорение точки за это время . (3)
. (3)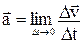 .
.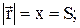
 . Законы изменения скорости и перемещения с течением времени имеют вид:
. Законы изменения скорости и перемещения с течением времени имеют вид: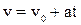 (4)
(4)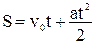 (5)
(5)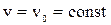 . В уравнениях (4) и (5) нужно положить
. В уравнениях (4) и (5) нужно положить  . При равноускоренном движении (v > v0) во всех формулах кинематики следует считать a > 0, а при равнозамедленном a < 0.
. При равноускоренном движении (v > v0) во всех формулах кинематики следует считать a > 0, а при равнозамедленном a < 0.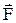 , называемой равнодействующей данных сил:
, называемой равнодействующей данных сил:  .
.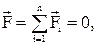
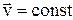 .
. или
или 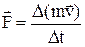 , где
, где 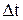 – промежуток времени, в течение которого произошло изменение импульса
– промежуток времени, в течение которого произошло изменение импульса 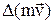 под действием силы
под действием силы 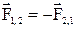


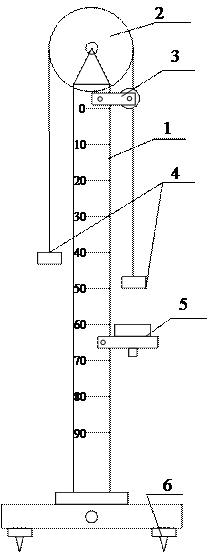 Машина Атвуда состоит из следующих основных узлов и деталей: корпуса (1), узла блока (2), электромагнитного пускателя (3), грузов (4), приемного столика (5), подставки (6).
Машина Атвуда состоит из следующих основных узлов и деталей: корпуса (1), узла блока (2), электромагнитного пускателя (3), грузов (4), приемного столика (5), подставки (6). (1)
(1)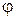 – угол, на который отклонена линия ОА от вертикали.
– угол, на который отклонена линия ОА от вертикали. или
или  , (2)
, (2) , находим:
, находим: . (3)
. (3) через
через  (w – круговая частота), мы приведем уравнение к виду:
(w – круговая частота), мы приведем уравнение к виду: . (4)
. (4) . (5)
. (5) . (6)
. (6) , то наибольшее смещение маятника от положения равновесия, называемое амплитудой колебаний
, то наибольшее смещение маятника от положения равновесия, называемое амплитудой колебаний  . Величину wt + j
. Величину wt + j 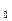 называют фазой колебаний с круговой частотой
называют фазой колебаний с круговой частотой  и периодом
и периодом  .
. , можно видеть, что физический маятник колеблется с тем же периодом, что и математический, имеющий длину
, можно видеть, что физический маятник колеблется с тем же периодом, что и математический, имеющий длину  . Длина математического маятника, имеющего тот же период колебания, что и физический, называется приведенной длиной данного физического маятника.
. Длина математического маятника, имеющего тот же период колебания, что и физический, называется приведенной длиной данного физического маятника. и
и 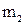 движутся до соударения со скоростями
движутся до соударения со скоростями  и
и  , а после соударения – со скоростями
, а после соударения – со скоростями  и
и  соответственно. Применяя законы сохранения импульса и энергии, можно записать:
соответственно. Применяя законы сохранения импульса и энергии, можно записать: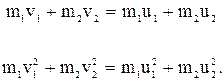 (1)
(1) (2)
(2) . (3)
. (3) (4)
(4) (5)
(5) (6)
(6) (7)
(7)
 и т.д.) из уравнений (7) получаем:
и т.д.) из уравнений (7) получаем: (8)
(8) (9)
(9) ;
;  (10)
(10)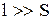 из этих уравнений получаем:
из этих уравнений получаем: (11)
(11) (12)
(12) – расстояние, проходимое шаром после n-го удара,
– расстояние, проходимое шаром после n-го удара,  – расстояние, проходимое шаром до первого соударения.
– расстояние, проходимое шаром до первого соударения. (13)
(13)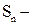 амплитуда n-го колебания шара без соударения, q – некоторая постоянная
амплитуда n-го колебания шара без соударения, q – некоторая постоянная  .
. , откуда
, откуда  , т.е. для определения коэффициента восстановления получаем следующую формулу, учитывающую силы трения
, т.е. для определения коэффициента восстановления получаем следующую формулу, учитывающую силы трения (14)
(14)

 Предположим, твердое тело А может вращаться вокруг некоторой неподвижной оси. Для того чтобы вызвать вращение тела (изменить его угловую скорость), необходимо внешнее воздействие. Однако сила
Предположим, твердое тело А может вращаться вокруг некоторой неподвижной оси. Для того чтобы вызвать вращение тела (изменить его угловую скорость), необходимо внешнее воздействие. Однако сила  , направление которой проходит через ось вращения, или
, направление которой проходит через ось вращения, или  , параллельная оси вращения, не могут изменить угловую скорость тела. Поэтому из приложенной к телу внешней силы R необходимо выделить составляющие
, параллельная оси вращения, не могут изменить угловую скорость тела. Поэтому из приложенной к телу внешней силы R необходимо выделить составляющие  Заметим, что при вращении тела составляющие
Заметим, что при вращении тела составляющие  , которую совершает вращающая сила, если точка приложения ее смещается по окружности радиуса r на
, которую совершает вращающая сила, если точка приложения ее смещается по окружности радиуса r на  . Предположим, что величина силы F при этом остается постоянной. Тогда
. Предположим, что величина силы F при этом остается постоянной. Тогда (1)
(1) , следовательно, работа, совершаемая вращающим моментом, равна произведению этого момента на угол поворота тела:
, следовательно, работа, совершаемая вращающим моментом, равна произведению этого момента на угол поворота тела: (2)
(2) ;
;  . (3)
. (3) и
и  , они ориентированы по оси вращения в одну и ту же сторону. Связь между величиной вращающего момента и величиной сообщаемого им углового ускорения можно получить следующим образом.
, они ориентированы по оси вращения в одну и ту же сторону. Связь между величиной вращающего момента и величиной сообщаемого им углового ускорения можно получить следующим образом. . Тогда для вращающегося тела, согласно формуле
. Тогда для вращающегося тела, согласно формуле  , имеем:
, имеем: (4)
(4) получаем:
получаем: . (5)
. (5) , (6)
, (6) расстояние от элемента массы до оси вращения, V – объем тела. Интегрирование производится по всему объему тела. Таким образом, момент инерции зависит не только от массы тела, но и от ее распределения относительно оси вращения.
расстояние от элемента массы до оси вращения, V – объем тела. Интегрирование производится по всему объему тела. Таким образом, момент инерции зависит не только от массы тела, но и от ее распределения относительно оси вращения.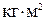 .
. (1)
(1) к первоначальному значению величины x, характеризующей размеры или объем тела:
к первоначальному значению величины x, характеризующей размеры или объем тела: (2)
(2) (3)
(3)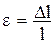 .
. . (4)
. (4) . (5)
. (5)
 , где х – колеблющаяся величина (смещение, скорость, сила и т.д.); t – время; х0 – амплитуда, w – круговая частота; j – начальная фаза. Величина
, где х – колеблющаяся величина (смещение, скорость, сила и т.д.); t – время; х0 – амплитуда, w – круговая частота; j – начальная фаза. Величина 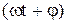 называется фазой колебаний.
называется фазой колебаний. .
. Математический маятник представляет собой точечное тело массой m, подвешенное на невесомой и нерастяжимой нити длиной l. Размеры тела малы по сравнению с длиной нити, а масса велика по сравнению с массой нити.
Математический маятник представляет собой точечное тело массой m, подвешенное на невесомой и нерастяжимой нити длиной l. Размеры тела малы по сравнению с длиной нити, а масса велика по сравнению с массой нити. , (1)
, (1)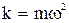 . Направление силы совпадает с направлением ускорения, а вектор ускорения при гармонических колебаниях всегда направлен к положению равновесия.
. Направление силы совпадает с направлением ускорения, а вектор ускорения при гармонических колебаниях всегда направлен к положению равновесия. на направление движения тела. Имеем
на направление движения тела. Имеем 
 , где a выражается в радианах. Так как эта сила всегда направлена к положению равновесия и поэтому имеет знак противоположный знаку х, то
, где a выражается в радианах. Так как эта сила всегда направлена к положению равновесия и поэтому имеет знак противоположный знаку х, то , (2)
, (2)
 ;
;  ;
;  (3)
(3) и
и  колебаний маятников каких-либо длин
колебаний маятников каких-либо длин  и
и  соответственно. Тогда, применив формулу (3), имеем:
соответственно. Тогда, применив формулу (3), имеем:  и
и  . Возводя оба равенства в квадрат и вычитая из первого равенства второе, получим:
. Возводя оба равенства в квадрат и вычитая из первого равенства второе, получим:  , откуда
, откуда (4)
(4) Физическим маятником называется тяжелое тело (т.е. находящееся в поле силы тяжести), имеющее ось вращения, не проходящую через центр масс.
Физическим маятником называется тяжелое тело (т.е. находящееся в поле силы тяжести), имеющее ось вращения, не проходящую через центр масс. (5)
(5) где
где  – расстояние от точки подвеса до центра тяжести. При малых углах отклонения
– расстояние от точки подвеса до центра тяжести. При малых углах отклонения  (в радианах), тогда возвращающий момент
(в радианах), тогда возвращающий момент
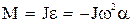 . (7)
. (7) , откуда
, откуда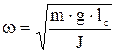 ;
;  . (8)
. (8) . (9)
. (9) – расстояние от оси качания до центра масс маятника. Величина
– расстояние от оси качания до центра масс маятника. Величина  называется приведенной длиной физического маятника, т.е. длиной такого математического маятника, который имеет период колебаний, равный периоду колебаний данного физического маятника.
называется приведенной длиной физического маятника, т.е. длиной такого математического маятника, который имеет период колебаний, равный периоду колебаний данного физического маятника. пропорциональная смещению тела от положения равновесия (k – коэффициент пропорциональности), и
пропорциональная смещению тела от положения равновесия (k – коэффициент пропорциональности), и 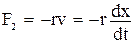 – сила трения, пропорциональная скорости тела (r – коэффициент пропорциональности). Уравнение движения будет иметь вид:
– сила трения, пропорциональная скорости тела (r – коэффициент пропорциональности). Уравнение движения будет иметь вид: , (1)
, (1)
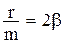 . (2)
. (2) (3)
(3) , (4)
, (4) ,
,  начальная амплитуда,
начальная амплитуда,  собственная круговая частота, w – круговая частота затухающих колебаний.
собственная круговая частота, w – круговая частота затухающих колебаний. ) будет с течением времени изменяться по экспоненциальному закону
) будет с течением времени изменяться по экспоненциальному закону  . Величина
. Величина (5)
(5) , (6)
, (6)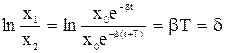 , (7)
, (7)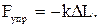 Следовательно,
Следовательно, , (8)
, (8) величина упругой деформации (удлинения пружины под действием веса груза), k – коэффициент упругости пружины, из (8) равный
величина упругой деформации (удлинения пружины под действием веса груза), k – коэффициент упругости пружины, из (8) равный


