
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение законов вращательного движения и определение момента силы тренияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: построить для маховика график зависимости углового ускорения b от момента силы натяжения М н и определить из него момент силы трения М тр и момент инерции маховика J. Оборудование: маховик, штангенциркуль, набор грузов, секундомер, линейка. Общие сведения
Согласно основному уравнению динамики вращательного движения угловое ускорение прямо пропорционально сумме моментов внешних сил, действующих на тело, и обратно пропорционально моменту инерции
Здесь В настоящей работе экспериментально изучается эта зависимость.
Описание установки и метода измерений
Маховик состоит из диска 1 и шкива 2, насаженных на вал (рис. 1). Вал может вращаться около горизонтальной оси OO'. На шкив намотана нить, к свободному концу которой подвешен груз 3. При падении груза маховик начинает вращаться с угловым ускорением b. Результирующий момент, создающий это ускорение, складывается из момента М н силы натяжения нити и момента М тр силы трения в подшипниках вала. Так как направления этих моментов противоположны, то уравнение (1) можно представить в виде
Если момент инерции маховика и момент силы трения остаются постоянными, то зависимость углового ускорения от момента силы натяжения линейная и графически изображается прямой линией (рис 2).
где r и D – радиус и диаметр шкива. Так как груз движется из состояния покоя равноускоренно, то
где h – путь, пройденный грузом за время t. Подставив выражение (4) в уравнение (3), получим формулу, по которой можно рассчитать на опыте угловое ускорение маховика
Модуль момента силы натяжения числено равен произведению силы натяжения F н на плечо силы, которое является радиусом шкива:
Силу натяжения нити найдем, рассматривая движение груза3. На него действуют сила тяжести P и сила реакции нити F 1. По второму закону Ньютона Учитывая, что сила натяжения нити, действующая на шкив и сила реакции, действующая на груз, одинаковы по величине (F н = F 1), получим
Тогда
Подставив в уравнение (6) выражение (4) для ускорения a, получим формулу
по которой можно рассчитать на опыте момент силы натяжения нити, действующей на маховик.
Порядок выполнения работы
1. Измерить штангенциркулем диаметр D шкива. 2. Вращая маховик, поднять висящий на нити груз на высоту h. Измерить высоту с помощью линейки (отсчет вести по нижнему основанию груза). 3. Отпустив маховик и, одновременно включив секундомер, определить время t опускания груза с высоты h. Измерение времени провести три раза. Результаты опыта занести в табл. 1. Таблица 1
4. Повторить опыт с пятью различными грузами. Массы грузов указаны на них. 5. По формулам (5) и (7) вычислить для каждого груза угловое ускорение b и момент силы натяжения М н, их значения записать в табл. 1. (При вычислении в формулы подставлять среднее значение времени
7. Продлить прямую до пересечения с осью абсцисс, определить по графику момент силы трения. Для определения момента инерции маховика нужно на экспериментальной прямой, взять точки A и B и провести через них прямые, параллельные осям координат (рис. 3). Момент инерции рассчитать по формуле
Записать окончательные результаты опыта
М тр =.....; J =......
Контрольные вопросы
1. Что называется моментом инерции материальной точки? Единицы его измерения. От чего зависит момент инерции тела? Какую роль он играет во вращательном движении? 2. Что называется моментом силы относительно точки, неподвижной оси? Как определить направление момента силы? В каких единицах он измеряется? 3. Дать определения угловой скорости и углового ускорения. Как определить их направления? 4. Какова связь между линейными и угловыми скоростями и ускорениями? 5. Вывести основное уравнение динамики вращательного движения. 6. Какие силы сообщают вращающий момент маховику? 7. Почему движение подвешенного к нити груза и вращение маховика являются равноускоренными? 8. Вывести расчетные формулы (5) и (7). 9. Объяснить, как графически находят момент силы трения и момент инерции маховика. 10. Проведите аналогию между величинами и формулами, описывающими поступательное и вращательное движение.
Библиографический список
1. Детлаф, А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. – М.: Высш. шк., 1999. – § 4.1–4.3. 2. Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 6, 16, 18. 3. Савельев, И. В. Курс общей физики в 3-х т. Т.1 / И. В. Савельев. – СПб.: Лань, 2005. – § 38, 39. 4. Кингсеп, А. С. Основы физики: в 2-х т. Т. 1 / А. С. Кингсеп, Г. Р. Локшин, О. А. Ольхов. – М.: Физматлит, 2001. – Гл.7 § 7.1, 7.3, 7.4, 7.6. 5. Сивухин, Д.В. Общий курс физики: в 5-ти т. Т.1 / Д. В. Сивухин. – М.: Физматлит МФТИ, 2005. – § 30, 32–38. 6. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 1.6 § 1.31– 1.34.
ЛАБОРАТОРНАЯ РАБОТА № 9
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.233.198 (0.009 с.) |


 – векторная сумма моментов сил, которую называют результирующим моментом сил; J – момент инерции тела.
– векторная сумма моментов сил, которую называют результирующим моментом сил; J – момент инерции тела.

 Из уравнения (2) следует, что при покоящемся маховике (b=0) М н = М тр. Только когда момент силы натяжения становится больше максимального момента силы трения покоя, маховик начинает вращаться равноускоренно. Прямая на графике пересекает ось абсцисс (рис. 2) в точке, которая определяет М тр. Угловое ускорение маховика b можно найти, зная тангенциальное ускорение
Из уравнения (2) следует, что при покоящемся маховике (b=0) М н = М тр. Только когда момент силы натяжения становится больше максимального момента силы трения покоя, маховик начинает вращаться равноускоренно. Прямая на графике пересекает ось абсцисс (рис. 2) в точке, которая определяет М тр. Угловое ускорение маховика b можно найти, зная тангенциальное ускорение  точек боковой поверхности шкива, которое равно ускорению a падающего груза:
точек боковой поверхности шкива, которое равно ускорению a падающего груза:



 , где m – масса подвешенного к нити груза.
, где m – масса подвешенного к нити груза.






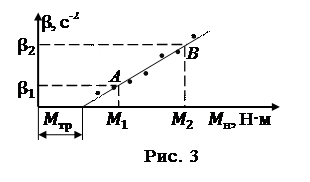 6. Результаты опыта изобразить графически на листе миллиметровой бумаги. Для этого по оси ординат в определенном масштабе отложить значения b, а по оси абсцисс также в определенном масштабе – значения Мн (масштабы по осям координат выбираются независимо друг от друга и должны быть нанесены на координатные оси). Полученные точки соединить прямой линией. Проводить прямую следует так, чтобы она лежала возможно ближе к точкам и по обе ее стороны оказывалось приблизительно равное их количество (см. рис. 3).
6. Результаты опыта изобразить графически на листе миллиметровой бумаги. Для этого по оси ординат в определенном масштабе отложить значения b, а по оси абсцисс также в определенном масштабе – значения Мн (масштабы по осям координат выбираются независимо друг от друга и должны быть нанесены на координатные оси). Полученные точки соединить прямой линией. Проводить прямую следует так, чтобы она лежала возможно ближе к точкам и по обе ее стороны оказывалось приблизительно равное их количество (см. рис. 3).



