
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент завинчивания в резьбеСодержание книги
Поиск на нашем сайте
Моментом завинчивания T з называется момент, который следует приложить к гайке для того, чтобы собрать соединение. Он склады- вается из двух составляющих:
где T т – момент сил трения на опорном торце гайки; для условий лабораторной работы T т = 0; Tp – момент сопротивления (сил трения) в резьбе
Самоторможение и КПД винтовой пары Самоторможение в винтовой паре проявляется в том, что стати- ческая осевая нагрузка не вызывает самоотвинчивания гайки. Это условие выражается неравенством ψ < φ¢. Все крепежные резьбы выполняют самотормозящими.
Для крепежных резьб понятие КПД не имеет смысла, а для резь- бовой пары передачи винт-гайка стремятся получить высокие зна- чения КПД.
Таблица 7.2 – Коэффициенты трения в резьбе f пары винт-гайка
Порядок выполнения работы 1. Получить у преподавателя или инженера узел с передачей винт-гайка. 2. Произвести измерение геометрических параметров. 3. Рассчитать геометрические параметры, измерения которых не- возможно произвести имеющимися средствами измерения. 4. Ознакомиться с принципом действия установки. 5. Произвести измерения перемещения при свободном хомуте. 6. Произвести измерения перемещения гайки при зажатом хомуте. 7. Определить разницу перемещений. 8. Оформить отчет.
Содержание отчета 1. Титульный лист. 2. Цели и задачи выполнения работы. 3. Оборудование и принадлежности к работе. 4. Схема передачи винт-гайка. 5. Результаты измерения геометрических параметров. 6. Результаты измерений перемещений. 7. Выводы. Контрольные вопросы 1. Дайте определение передачи винт-гайка. 2. Основные параметры передачи винт-гайка. 3. Виды винтовых механизмов. 4. Типы резьб. 5. Геометрические параметры резьбы. 6. 7. Материалы, применяемые для изготовления деталей резьбовых соединений. Литература 1. Иванов, М. Н. Детали машин / М. Н. Иванов, В. Н. Финогенов. – М.: Высшая школа, 2003. – 408 с. 2. Орлов, П. И. Основы конструирования: справочно-методичес- кое пособие: в 2 кн. / П. И. Орлов. – М.: Машиностроение, 1988. – Кн. 2. – 544 с. 3. Проектирование механических передач / С. А. Чернавский [и др.]. – М.: Машиностроение, 1984. – 560 с.
Лабораторная работа № 8 ИЗУЧЕНИЕ МАЛЬТИЙСКОГО МЕХАНИЗМА Цель работы: изучение конструкции мальтийского механизма и конструктивных особенностей его различных видов. Оборудование и принадлежности 1. Узел, содержащий мальтийский механизм. 2. Штангенциркуль. 3. Линейка. 4. Отвертка Теоретические положения Общие сведения Мальтийские механизмы применяются для преобразования обычно равномерного вращательного движения ведущего звена-кривошипа в периодические повороты с остановками определенной продолжи- тельности ведомого звена-креста. КПД механизмов h = 0,75–0,85. По конструкции мальтийские механизмы бывают: 1) плоские и пространственные; 2) с внешним зацеплением и с внутренним; 3) с одним кривошипом и с несколькими.
Плоский механизм с внешним зацеплением и четырехпазовым крестом показан на рисунке 8.1. Ведущим звеном является криво- шип 1, а ведомым – крест 2. Число радиальных пазов z креста быва- ет от 3 до 12. При вращении кривошипа 1 цевка А входит в паз креста 2 и по- ворачивает его на угол 2α0 = 2 p / z. Когда цевка А выходит из паза, крест останавливается и фиксируется секторным замком. Выпуклая цилиндрическая поверхность замка входит в соприкосновение с во- гнутой поверхностью креста и препятствует повороту последнего до тех пор, пока цевка А кривошипа не войдет в следующий паз креста. Кривошип и крест вращаются в противоположных направ- лениях. За один полный оборот кривошипа с одной цевкой крест делает 1/ z оборота и остановку.
Механизм с внутренним зацеплением и четырехпазовым крестом показан на рисунке 8.2. Ведущим звеном является кривошип, цевка А которого, входя в радиальный паз креста, поворачивает его на угол
Механизмы с внутренним зацеплением работают с меньшими угловыми ускорениями креста, чем механизмы с внешним зацепле- нием при одинаковом числе пазов креста.
На рисунке 8.3 показана схема сферического мальтийского меха- низма. Такие механизмы могут быть построены с различными угла- ми b между валами кривошипа и креста. Обычно этот угол берется равным 90°. Преимущество сферических мальтийских механизмов по сравнению с плоскими заключается, прежде всего, в возможно- сти передачи периодических движений между взаимно перпендику- лярными валами, что удобно для компоновки привода в машине. Кроме того, ускорения, а следовательно, и инерционные нагрузки в
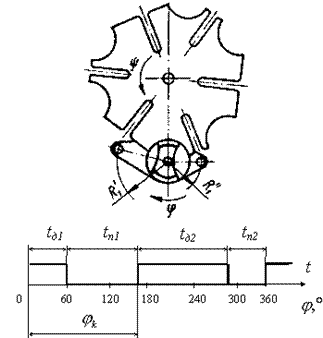
Мальтийские механизмы с несколькими кривошипами и несколь- кими пальцами имеют различные длительности времени покоя и вре- мени движения. На рисунке 8.4, а показан четырехпазовый мальтий- ский механизм с двумя кривошипами одинаковой длины. Кривоши- пы расположены между собой под углом γк (угол γк на рисунке 8.4 не показан). На рисунке 8.4, б показана временная диаграмма поворота шайбы мальтийского креста, из которой видно, что ведомое звено соверша- ет прерывистое движение. Если положение ведущего звена, изобра- женное на рисунке, принять за начало отсчета, то в течение време- ни t д1 крест повернется на 90°. Затем последует пауза продолжитель- ностью t п1.Длительностьпаузыпропорциональнаразностиγк – 90°.Далее в течение промежутка времени t д2 мальтийский крест опять повернется на 90° и остановится на время t п2, равное 270° – γк. Если в рассматриваемом примере γк = 180°, то t п1 = t п2 = t д1 = t д2. Таким
На рисунке 8.5 изображен мальтийский механизм с шестью па- зами и двумя кривошипами разной длины. Более длинный криво- шип R¢ 1 обеспечивает поворот шайбы мальтийского креста на 120°. Более короткий кривошип R¢ 1 поворачивает крест на угол 60°. Таким образом, ведомое звено получает пульсирующее движение с разны- ми t д1 и t д2. Длительности пауз определяются так же, как и в преды- дущем примере. Соотношение между t п1 и t п2 зависит от величины центрального угла γк между кривошипами. Находят применение механизмы, в которых ползун с пазами пе- ремещается под действием непрерывно вращающегося кривошипа. Такой механизм можно рассматривать как мальтийский с бесконеч- но большим числом пазов. Ползун движется по косинусоидальному закону изменения ускорения. Этот закон движения является проме- жуточным между законами движения креста с внешним и внутрен- ним зацеплениями.
Мальтийский механизм представляет собой частный случай меха- низма с качающейся кулисой. На рисунке 8.6 условно показан один паз мальтийского креста, вращающегося вокруг центра О 2. В зави- симости от того, с какой частью ведомой кулисы соприкасается цевка кривошипа во время рабочего хода, мальтийские механизмы могут иметь внешнее В и внутреннее В' зацепления. В механизмах внешнегозацепления(МВнешЗ)точка П пересечениянормали nn с меж- осевой линией не выходит за пределы ее участка О 1 О 2, поэтому ве- дущее и ведомое звенья вращаются в противоположных направле- ниях. В механизмах внутреннего зацепления (МВнутЗ), наоборот, точ- ка П' располагается вне отрезка О 1 О 2, поэтому угловые скорости ведущего и ведомого звеньев в любом положении имеют один знак.
Чтобы поворот креста проходил без жестких ударов в начале и конце поворота, угловая скорость креста в эти моменты должна быть равна нулю. При этом вектор скорости ролика будет направлен вдоль паза, а кривошип с пазом мальтийского креста образует прямой угол. Треугольник ООВ – прямоугольный (см. рисунок 8.6), т. е. π
Угол между осями пазов креста
2π
z где z – число пазов. Тогда угол поворота кривошипа 2b, соответствующий повороту креста на угол 2a, будет равен: – для механизма с внешним зацеплением
–
Время покоя можно определить как разность t ï = T ê - t ä. Тогда
Частота вращения кривошипа определяется из тех соображений, что время пребывания креста в покое должно быть не меньше времени наиболее длительной (лимитирующей) технологической операции, при которой поворачиваемая часть машины остается неподвижной. Исследуем зависимость коэффициента производительности маль- тийского механизма от числа пазов. По определению коэффициент производительности представляет собой отношение времени рабо- чих движений к времени рабочего цикла. Как правило, рабочие дви- жения выполняются во время выстоя карусели или конвейера. Для
В таблице 8.1 приведены значения коэффициентов производитель- ности h, углов α и β в зависимости от числа пазов креста. Рассмот- рено внешнее и внутреннее зацепления. Таблица 8.1 – Производительность мальтийского механизма
Таким образом, для механизма с внешним зацеплением с увеличе- нием числа пазов КПД уменьшается, а для механизма с внутренним зацеплением – растет. Для МВнешЗ h всегда больше 0,5, для МВнутЗ h всегда меньше 0,5, т. е. мальтийские механизмы с внешним зацеп- лением с точки зрения производительности более эффективны, чем механизмы с внутренним зацеплением.
Порядок выполнения работы 1. Получить у преподавателя узел, содержащий мальтийский механизм. 2. Провести эскизирование мальтийского механизма. 3. Ознакомиться с лабораторной установкой. 4. Включить установку и секундомер. 5. Зафиксировать с помощью секундомера время движения вы- ходного вала (20 измерений). 6. Зафиксировать с помощью секундомера время покоя выход- ного вала (20 измерений). 7. 8. Найти отношение времени покоя и времени движения. 9. Определить отношение времени покоя ко времени движения на основании формул. 10. Сравнить полученные значения с экспериментальными.
Контрольные вопросы 1. Для чего применяются мальтийские механизмы? 2. Какие бывают мальтийские механизмы по конструкции? 3. Расскажите о принципе действия плоского механизма с внеш- ним зацеплением. 4. Расскажите о принципе действия механизма с внутренним за- цеплением. 5. Расскажите о конструктивных особенностях сферического мальтийского механизма. Чем отличается сферический мальтийский механизм от плоского механизма? 6. Расскажите о принципе действия мальтийского механизма с несколькими кривошипами и несколькими пальцами. 7. От чего зависит зацепление мальтийского механизма? 8. Чему равно время движения мальтийского креста механизма? 9. Что необходимо для того, чтобы поворот креста проходил без жестких ударов в начале и конце поворота? Куда будет направ- лен вектор скорости ролика? 10. Чему равен коэффициент производительности мальтийского механизма? 11. Сравните мальтийские механизмы с внешним и внутренним зацеплением с точки зрения производительности.
Литература 1. Элементы приборных устройств: учебное пособие для сту- дентов вузов: в 2 ч. / О. Ф. Тищенко [и др.]; под ред. О. Ф. Тищен- ко. – М.: Высшая школа, 1982. – Ч. 1: Детали, соединения и пере- дачи. – 304 с. 2.
Учебное издание
ДЕТАЛИ И МЕХАНИЗМЫ ПРИБОРОВ Лабораторный практикум для студентов специальностей 1-38 01 01 «Механические и электромеханические приборы и аппараты», 1-38 02 02 «Биотехнические и медицинские аппараты и системы», 1-52 02 01 «Технология и оборудование ювелирного производства» Составители: КОРЗУН Павел Олегович НОВИКОВ Александр Анатольевич
Редактор В. О. Кутас Компьютерная верстка Н. А. Школьниковой Подписано в печать 21.03.2013. Формат 60´84 1/16. Бумага офсетная. Ризография. Усл. печ. л. 5,46. Уч.-изд. л. 4,27. Тираж 100. Заказ 1554.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 150; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.118 (0.009 с.) |

 Практический интерес представляет такой параметр, как коэф- фициент полезного действия η винтовой пары:
Практический интерес представляет такой параметр, как коэф- фициент полезного действия η винтовой пары: В таблице 7.2 приведены справочные данные о коэффициентах трения.
В таблице 7.2 приведены справочные данные о коэффициентах трения.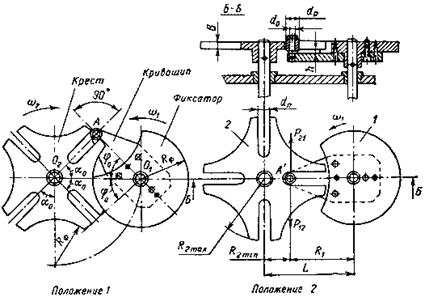



 Основные характеристики плоских мальтийских механизмов
Основные характеристики плоских мальтийских механизмов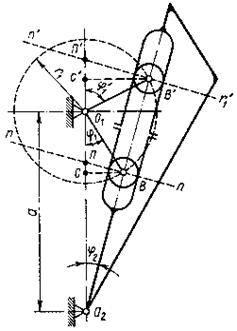
 α + β =.
α + β =.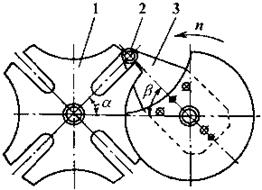
 2α =,
2α =,
 для механизма с внутренним зацеплением
для механизма с внутренним зацеплением
 В большинстве случаев мальтийские механизмы используются в многопозиционных машинах и задают время рабочего цикла. При этом Т р = Т к = 60 / n к, где n к – частота вращения кривошипа. Обозна- чим t д – время движения мальтийского креста, t л – время покоя кре-
В большинстве случаев мальтийские механизмы используются в многопозиционных машинах и задают время рабочего цикла. При этом Т р = Т к = 60 / n к, где n к – частота вращения кривошипа. Обозна- чим t д – время движения мальтийского креста, t л – время покоя кре-

 ста. Для механизма (МВнешЗ) время движения креста пропорциональ- но величине угла b. Составим пропорцию (8.3) и найдем t д:
ста. Для механизма (МВнешЗ) время движения креста пропорциональ- но величине угла b. Составим пропорцию (8.3) и найдем t д:




 Для механизма с внутренним зацеплением
Для механизма с внутренним зацеплением
 z
z





