
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание установки и метода Клемана и Дезорма.Содержание книги
Поиск на нашем сайте
Если при помощи насоса накачать в баллон некоторое количество воздуха, то его давление и температура повысятся. Вследствие теплообмена с окружающей средой температура воздуха в баллоне через некоторое время сравняется с температурой окружающей среды. Давление p 1, установившееся в баллоне, больше атмосферного на величину, определяемую разностью уровней h 1 жидкости в коленах манометра (рис. 1). p и h измеряются в мм водяного столба.
p 1 = p атм + h 1.
На рис. 2 данному сoстоянию соответствует точка A. Если открыть на короткое время кран К, то воздух в баллоне расширится. Давление внутри баллона в конце расширения сравняется с атмосферным (обозначим его через p 2 = p атм, объем рассматриваемой массы воздуха равен объему сосуда V 2. Так как процесс быстрого расширения воздуха можно считать адиабатическим, то температура газа T 2 станет ниже комнатной. Следовательно, в конце адиабатического расширения (точка B на рис. 2) параметры газа будут p 2, V 2, T 2. Применяя к этому состоянию уравнение Пуассона, получим:
Охладившийся при расширении воздух в баллоне через некоторое время, вследствие теплообмена, нагреется до комнатной температуры (процесс нагревания является изохорическим). Поэтому давление воздуха возрастет до некоторой величины p 3. Это давление будет больше атмосферного на величину, определяемую разностью уровней жидкости в коленах манометра h 2. Параметры этого состояния (точка C на рис. 2):
p 3, V 3, T 3= T комн, p 3 = p 2 + h 2.
На графике рис. 2 показаны процессы перехода газа из одного состояния в другое. Линия AB является адиабатой, BC – изохорой, AC – изотермой. Так как переход газа из состояния A в состояние B происходит адиабатически, то он подчиняется уравнению Пуассона (
Дальнейший переход из состояния B в состояние C может быть охарактеризован уравнением Гей-Люссака (изохорический процесс):
Исключив из уравнений (6) и (7) температуру и учтя, что T 1= T 3, получим
Подставляя в (8) значения давлений p 1 и p 3, выраженные через давление p 2 и разность столбов жидкости в манометре (p 1 = p 2 + h 1, p 3 = p 2 + h 2), получим
В условиях эксперимента h 1/ p 2и h 2/ p 2 значительно меньше единицы, поэтому можно ограничиться лишь двумя первыми членами биномов Ньютона, что дает
Отсюда можно получить расчетную формулу для коэффициента Пуассона:
Порядок выполнения работы.
1. Проверить, нет ли утечки газа из баллона. Для этого с помощью поршневого насоса медленно нагнетают в баллон воздух. За повышением давления воздуха в баллоне наблюдают по разности уровней в коленах манометра. Так как при нагнетании воздуха температура его несколько повысится, следует подождать 2-3 минуты, пока установится тепловое равновесие с окружающей средой. После этого, если показания манометра не изменяются (нет утечки воздуха), записывают значение h 1, соответствующее исходному состоянию (A). 2. Открыть клапан-кран (К), соединяя воздух в баллоне с атмосферой. Как только выровняется давление воздух внутри баллона с атмосферным (прекратится шипение воздуха), клапан-кран быстро закрыть, или при отсутствии клапана-крана пережать резиновую трубку. Предполагается, что этот процесс соответствует адиабате АВ (рис. 2). Давление воздуха в баллоне понизится до атмосферного, а газ охладится. Однако, в результате теплообмена с окружающей средой через 2-3 минуты после закрытия клапана-крана газ изохорически перейдет в состояние C. Давление воздуха в баллоне возрастет и появится разность уровней h 2в коленах манометра. Указанный эксперимент повторить 5-6 раз. Результаты измерений h 1 и h 2 записать в табл. 1. 3. По формуле (9) вычислить 4. Вычислить абсолютную и относительную погрешность по формуле:
Таблица 1
5. Записать конечный результат в виде:
6. Рассчитать
Контрольные вопросы 1. Что называют удельной теплоемкостью и молярной теплоемкостью вещества? Какая связь между ними? 2. Теплоемкость – это функция состояния или функция процесса? 3. Чему равны молярные теплоемкости идеальных газов при изопроцессах? 4. Почему 5. Какое практическое значение имеет соотношение 6. Какой процесс называется адиабатическим и каким уравнением он описывается? 7. Какова связь между параметрами, характеризующими состояние газа при адиабатическом процессе? 8. Изобразите график процессов, происходящих в данной работе, в координатах p и V и назовите эти процессы. Изобразите графики известных вам процессов в координатах p и Т, Т и V. 9. От каких параметров зависит внутренняя энергия идеального газа? 10. Как формулируется первое начало термодинамики и как оно записывается аналитически? Как записать его для различных изопроцессов? 11. Выведите расчетную формулу для вычисления 12. Почему необходимо выждать некоторое время после того, как накачают воздух в баллон? 13. Почему после выхода воздуха из баллона и перекрытия клапана-крана возникающая разность уровней в коленах манометра зависит от скорости (времени) расширения газа? 14. Каковы отличия между реальным и идеальным газами?
Библиографический список 1. Курс физики: Учебник для вузов: в 2-х т. Т. 2 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 5.1 § 5.2 – 5.4 Гл. 5.2 § 5.17 – 5.19. 2. Савельев, И.В. Курс общей физики в 3-х т. Т.1 / И.В. Савельев. – СПб.:Лань, 2005. – § 82 – 86. 3. Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 50 – 56.
ЛАБОРАТОРНАЯ РАБОТА № 18 ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ВОЗДУХА ПО СКОРОСТИ РАСПРОСТРАНЕНИЯ ЗВУКА
Цель работы: определить показатель адиабаты воздуха по скорости распространения звука в воздухе. Оборудование: металлическая труба, микрофон, осциллограф, элетродинамический громкоговоритель (динамик), генератор электрических колебаний звуковой частоты.
Общие сведения
В воздухе, как и во всякой газообразной среде, могут распространяться только продольные волны. Поэтому звуковая волна в воздухе представляет собой чередование сжатий и разрежений. При сжатии увеличивается давление воздуха и, следовательно, возрастает его упругость. При разрeжении упругость воздуха уменьшается. Соответственно, при сжатии воздух нагревается, а при разрежении охлаждается. Эти изменения температуры приводят к добавочному изменению упругости воздуха (возрастание и уменьшение соответственно). Такие изменения температуры, вызывающие добавочное изменение упругости воздуха, возникают лишь тогда, когда сжатия и разрежение воздуха быстро сменяют друг друга, т.е. когда соседние участки воздуха не успевают обмениваться теплотой и процесс сжатия и разрежения воздуха близок к адиабатическому. Лаплас впервые доказал, что сжатия и разрежения в звуковой волне в воздухе происходят адиабатически и скорость звука в воздухе увеличивается благодаря изменениям температуры, производимым самой звуковой волной. Эти изменения температуры невелики и не влияют на среднюю температуру воздуха.
Пусть кратковременный импульс силы F (на рис. 1 показан стрелками), равномерно распределенной по сечению S, вызывает смещение вправо частиц среды (воздуха) в узком слое, прилегающему к этому сечению. Вследствие инертности, соседний к нему слой окажется деформированным и в нем возникнут упругие силы, стремящиеся остановить частицы первого слоя и привести в движение частицы второго слоя. В итоге действие упругих сил приведет к исчезновению деформации сжатия в этом слое и к ее возникновению в следующем слое. Таким образом, импульс деформации сжатия передается от слоя к слою с некоторой скоростью
Этому уплотнению соответствует масса:
и импульс:
где
скорость распространения импульса деформации сжатия. Можно полагать, что такой импульс будет соответствовать уплотнению во втором и последующих слоях воздуха (среда однородная). Приравняем этот импульс к импульсу внешней силы:
где d t – промежуток времени, в течение которого деформация сжатия охватывает слой d x. Изменение давления при деформации:
Отсюда скорость распространения звуковой волны:
T. е. скорость распространения звука определяется отношением изменения давления к изменению плотности в любой, сплошной, однородной и упругой среде. В дифференциальной форме:
При адиабатическом процессе объем и давление газа связаны уравнением Пуассона:
где
отношение теплоемкости газа при постоянном давлении к теплоемкости при постоянном объеме. Поскольку плотность газа обратно пропорциональна его объему, то:
Дифференцируя это выражение, получим
Отсюда:
Следовательно:
Это формула Лапласа. Хотя в последнюю формулу входит давление p, скорость звука от давления не зависит, т.к. изменение давления пропорционально изменению плотности воздуха. Скорость звука в воздухе зависит от температуры. Установим эту зависимость, воспользовавшись формулой Клапейрона-Менделеева для одного моля газа (воздуха):
Здесь
Следовательно,
т.к.
Здесь Из этой формулы:
Формула (10) является расчетной. Чтобы вычислить Для определения скорости звука в воздухе в этой работе используется метод стоячей волны. Процесс распространения колебаний в упругой среде называется волной. Расстояние, на которое распространяется волна за время, равное периоду колебания, называется длиной волны. Длина волны связана с периодом колебания частиц T и скоростью распространения волны
где
Рассмотрим стоячие волны, которые образуются в трубе с воздухом длиной l, закрытой с двух сторон (рис. 2а). Через небольшое отверстие в одном конце трубы при помощи динамика возбудим колебания звуковой частоты. Тогда в воздухе внутри трубы распространится звуковая волна, которая отразится от другого закрытого конца и побежит обратно. Казалось бы, что должна возникнуть стоячая волна при любой частоте колебаний. Однако, в трубе, закрытой с двух сторон, на концах должны образовываться узлы. Это условие выполняется, если в трубе укладывается половина длины бегущей волны: l = l/2 (рис. 2б). Здесь амплитуды смещения частиц воздуха отложены по вертикали. Сплошной линией изображена бегущая волна, пунктиром – отраженная. В трубе возможна и такая стоячая волна, где имеется и еще один узел, при этом укладываются две половины длины волны: l = 2l/2 (рис. 2в). Следующая стоячая волна возникает, когда длина бегущей волны удовлетворяет условию l = 3λ/2. Таким образом, в трубе, закрытой с двух сторон, стоячая волна образуется в тех случаях, когда на длине трубы укладывается целое число половин длин волн:
где k = 1, 2, 3.... Выразив l из (12) и подставив в формулу
Полученная формула выражает собственные частоты колебаний воздушного столба в трубе длиной l, где k = 1 соответствует основному тону, k = 2, 3, … – обертонам. В общем случае колебание столба воздуха может быть представлено как наложение собственных колебаний.
Описание установки
Общий вид установки показан на рис. 3. На конце металлической трубы 1 жестко закреплен микрофон 2. Вдоль трубы при помощи стержня 3 может свободно перемещаться электродинамический громкоговоритель 4. От генератора электрические колебания звуковой частоты подаются на динамик. Динамик возбуждает колебания воздуха определенной частоты.
Если с помощью генератора волн предельной частоты возбудить колебания воздуха в трубе, то при совпадении частоты генератора с одной из собственных частот воздушного столба наступает резонанс – в трубе установится стоячая волна. Это обнаруживается по увеличению громкости звука и максимальной амплитуде сигнала на экране осциллографа. Поскольку на закрытых концах трубы образуются узлы, а расстояние между соседними узлами равно l/2 (рис. 2), то усиление звука будет возникать всякий раз, как длина воздушного столба изменится на l/2. Следовательно, если при изменении столба воздуха на величину
Откуда
Скорость звука
Измерив в ходе опыта расстояния l 1 и l 2 при помощи линейки, закрепленной на трубе, и зная частоту n звукового генератора, по формуле (15) можно найти скорость звука в воздухе. Порядок выполнения работы
1. Подключить динамик к генератору электрических колебаний звуковой частоты, а микрофон – к осциллографу. Включить генератор и осциллограф в сеть. Частоту генератора задавать примерно 2-4 кГц. 2. При помощи стержня приблизить динамик вплотную к микрофону. 3. Медленно выдвигая стержень, по шкале, имеющейся на трубе, замерить длину воздушного столба l 1, соответствующую какому-либо максимуму звучания и максимальному значению амплитуды сигнала на экране осциллографа. Этот максимум принять за нулевой. Увеличивая далее расстояние между динамиком и микрофоном, считая последующие максимумы, взять отсчет длинны столба для некоторого n -го максимума (n брать порядка 4-6). Опыт повторить пять раз. Результаты записать в табл. 1. 4. По формуле (14) вычислить длину волны, а по (15) – скорость звука в воздухе. Найти среднее значение скорости 5. Среднее значение скорости, найденное по формуле (15), подставить в выражение (13) и вычислить
Таблица 1
Контрольные вопросы 1. Что называется волной? 2. Какие волны называются продольными и какие поперечными? 3. От чего зависит скорость распространения продольных и поперечных волн? 4. Написать и пояснить уравнение плоской бегущей волны. 5. Вывести уравнение стоячей волны. 6. Какие точки называются узлами, а какие пучностями? 7. В каких случаях в месте отражения получается узел, а в каких пучность? 8. Объяснить явление резонанса в воздушной трубе, закрытой с двух сторон. 9. Дать определение адиабатическому процессу. Привести пример. 10.Что такое постоянная адиабаты и какова ее связь со степенями свободы молекул. 11. Найти работу газа при адиабатическом процессе. 12. Вывести уравнения Лапласа. 13. Вывести связь между постоянной адиабаты и скоростью распространения звука в воздухе. Библиографический список 1. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 3.5 § 3.15, 3.18. Т.2 Гл. 5.1 § 5.2 – 5.4 Гл. 5.2 § 5.17 – 5.19 2. Детлаф, А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. – М.: Высш. шк., 1999. – § 29.1 – 29.4. 3. Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 140, 141, 153 – 158. 4. Савельев, И.В. Курс общей физики в 3-х т. Т.1 / И.В. Савельев. – СПб.: Лань, 2005. – § 82 – 83, 86 – 88. ЛАБОРАТОРНАЯ РАБОТА № 19
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1015; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.107.192 (0.012 с.) |

 Установка состоит из стеклянного баллона Б, поршневого насоса Н, водяного манометра М, клапана-крана К рис. 1. Роль клапана-крана на некоторых установках может выполнять резиновая трубка.
Установка состоит из стеклянного баллона Б, поршневого насоса Н, водяного манометра М, клапана-крана К рис. 1. Роль клапана-крана на некоторых установках может выполнять резиновая трубка. Если обозначить через m массу воздуха в баллоне при атмосферном давлении, то при давлении p 1 воздух займет меньший объем, чем объем сосуда. Обозначим этот объем через V 1. Тогда состояние воздуха массой m внутри баллона будет характеризоваться параметрами p 1, V 1, T 1= T комн.
Если обозначить через m массу воздуха в баллоне при атмосферном давлении, то при давлении p 1 воздух займет меньший объем, чем объем сосуда. Обозначим этот объем через V 1. Тогда состояние воздуха массой m внутри баллона будет характеризоваться параметрами p 1, V 1, T 1= T комн.
 ), которое в данном случае удобно записать в форме
), которое в данном случае удобно записать в форме





 для каждого опыта.
для каждого опыта.








 теоретически, считая воздух двухатомным газом. Сравнить экспериментальный результат с теоретическим. Объяснить расхождение результатов.
теоретически, считая воздух двухатомным газом. Сравнить экспериментальный результат с теоретическим. Объяснить расхождение результатов. ? Каков физический смысл универсальной газовой постоянной R?
? Каков физический смысл универсальной газовой постоянной R? .
. Определим скорость распространения звука в воздухе, считая его сплошной однородной упругой средой, плотность которой равна ρ. В этой среде мысленно выделим некоторый цилиндрический объем с площадью поперечного сечения S.
Определим скорость распространения звука в воздухе, считая его сплошной однородной упругой средой, плотность которой равна ρ. В этой среде мысленно выделим некоторый цилиндрический объем с площадью поперечного сечения S. , отличной от скорости смещающихся частиц воздуха. Пусть в начале деформация сжатия, охватывает слой воздуха толщиной d x, а средняя плотность среды в нем возрастает до
, отличной от скорости смещающихся частиц воздуха. Пусть в начале деформация сжатия, охватывает слой воздуха толщиной d x, а средняя плотность среды в нем возрастает до  .
. 











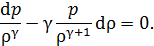



 – объём одного моля газа. Из этой формулы:
– объём одного моля газа. Из этой формулы:



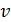 соотношением:
соотношением:
 = 1/ T – частота колебания частиц среды.
= 1/ T – частота колебания частиц среды. Если две волны одинаковой частоты и амплитуды распространяются навстречу друг другу, то в результате их наложения при определенных условиях может возникнуть стоячая волна. В среде, где установились стоячие волны, колебания частиц, происходят с различной амплитудой. В определенных точках среды амплитуда колебания равна нулю, эти точки называются узлами; в других точках амплитуда равна сумме амплитуд складываемых колебаний, такие точки называются пучностями. Расстояние между двумя соседними узлами (или пучностями) равно l/2, где l – длина бегущей волны (рис. 2). Стоячая волна может образоваться при наложении падающей и отраженной волн. При этом если отражение происходит от среды во много раз более плотной, чем среда, в которой распространяется волна, то в месте отражения смещение частиц равно нулю, то есть образуется узел. Если волна отражается от среды менее плотной, то из-за слабого задерживающего действия частиц второй среды на границе возникают колебания с удвоенной амплитудой, то есть образуется пучность. В том случае, когда плотности сред мало отличаются друг от друга, наблюдается частичное отражение волн от границы раздела двух сред.
Если две волны одинаковой частоты и амплитуды распространяются навстречу друг другу, то в результате их наложения при определенных условиях может возникнуть стоячая волна. В среде, где установились стоячие волны, колебания частиц, происходят с различной амплитудой. В определенных точках среды амплитуда колебания равна нулю, эти точки называются узлами; в других точках амплитуда равна сумме амплитуд складываемых колебаний, такие точки называются пучностями. Расстояние между двумя соседними узлами (или пучностями) равно l/2, где l – длина бегущей волны (рис. 2). Стоячая волна может образоваться при наложении падающей и отраженной волн. При этом если отражение происходит от среды во много раз более плотной, чем среда, в которой распространяется волна, то в месте отражения смещение частиц равно нулю, то есть образуется узел. Если волна отражается от среды менее плотной, то из-за слабого задерживающего действия частиц второй среды на границе возникают колебания с удвоенной амплитудой, то есть образуется пучность. В том случае, когда плотности сред мало отличаются друг от друга, наблюдается частичное отражение волн от границы раздела двух сред.
 , получим
, получим
 Звуковая волна, дойдя до микрофона, отражается от него (как от стенки). Сигнал от микрофона подается на осциллограф 6 для визуального наблюдения амплитуды звуковых колебаний воздушного столба в трубе.
Звуковая волна, дойдя до микрофона, отражается от него (как от стенки). Сигнал от микрофона подается на осциллограф 6 для визуального наблюдения амплитуды звуковых колебаний воздушного столба в трубе. наблюдалось n усилений звука, то
наблюдалось n усилений звука, то

 . Тогда, с учетом (14), получим конечную формулу для расчета скорости звука
. Тогда, с учетом (14), получим конечную формулу для расчета скорости звука
 .
.


