
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соотношение между силами и моментами, действующими на резьбовые детали в процессе затяжки.Содержание книги
Поиск на нашем сайте
Момент сопротивления в резьбе. Выявим соотношение между силой Tзат затяжки и моментом T р сопротивления в резьбе:
Из полученной зависимости следует, что момент сопротивления в резьбе тем больше, чем больше приведенный угол трения j1= j/cosgn т.е. Тр зависит от материала резьбовой пары и от угла g наклона рабочей стороны профиля. В метрической резьбе угол наклона профиля наибольший (g = 30°), поэтому и момент сопротивления в резьбе – наибольший. Для крепежных резьб это не является недостатком, поскольку момент сопротивления в резьбе препятствует самоотвинчиванию. Момент Тр сопротивления в резьбе скручивает стержень винта (создает касательные напряжения). Момент трения на торце гайки. Контакт гайки с плоской опорной поверхностью корпуса ограничен кольцом с внутренним диаметром, равным диаметру d0 отверстия в корпусе под стержень винта, и наружным диаметром D, соответствующим границе фаски на опорной поверхности гайки. Приближенно момент Tт трения на торце гайки определяют как произведение силы трения Fтр=Fзатfт на средний радиус Rcp = (d0 + D)/4 кольцевой поверхности:
Здесь fт– коэффициент трения на поверхности контакта. В большинстве резьбовых соединений должна быть обеспечена стабильная работа без самоотвинчивания. Условие самоторможения резьбы без учета трения на торце гайки по аналогии с наклонной плоскостью можно записать в виде
где y – угол подъема резьбы (1,5...3°); j1 – приведенный угол трения (при f =0,1...0,3 j1=6...16°). Отсюда следует, что все крепежные резьбы — самотормозящие. Но это только при статическом действии нагрузок. При вибрациях j1 уменьшается вследствие микроперемещений поверхностей трения, сминания микронеровностей на рабочих поверхностях резьбы, и резьбовая пара отвинчивается. Поэтому на практике широко применяют различные способы стопорения, в которых используют: · дополнительное трение в резьбе или на торце гайки (пружинные шайбы, контргайки, фрикционные вставки в винты или гайки); · фиксирующие детали (шплинты, проволоку, стопорные шайбы с лапками); · приварку или пластическое деформирование (расклепывание, кернение); · пасты, лаки, краски, герметики и клеи. Цилиндрические передачи Цилиндрические передачи с внешним зацеплением (рис. 35). Шестерня в понижающей передаче является ведущим элементом и всем ее параметрам присваивают индекс 1. Например, частота вращения n1, мин–1, число зубьев z1. Параметры ведомого элемента пары — колеса имеют индекс 2: n2, z2.
Линии пересечения боковых поверхностей зубьев с любой круговой цилиндрической поверхностью, соосной с начальной, называют линиями зубьев. Если линии зубьев параллельны оси зубчатого колеса, то его называют прямозубым (рис. 35,а).Если эти линии винтовые постоянного шага, то зубчатое колесо называют косозубым (рис. 35,б).С увеличением угла βнаклона зуба повышается нагрузочная способность передачи, но возрастает осевая сила, действующая на валы и опоры. Обычно β = 8...18°. Рисунок 35 – Цилиндрические передачи с внешним зацеплением Разновидность косозубых зубчатых колес — шевронные колеса: без канавки (рис. 35,в)и с канавкой для выхода инструмента (рис. 35,г).Вследствие противоположного направления зубьев на полушевронах осевые силы взаимно уравновешены на колесе и не нагружают опоры. Обычно β= 25...40°. Точку W касания начальных окружностей dw1 шестерни и dw2 колеса называют полюсом зацепления. Для простоты изложения будем рассматривать передачи без смещения, для зубчатых колес которых диаметры dw начальные и d делительные совпадают: d1 = dw1, d2 = dw2. Однако в обозначении межосевого расстояния для общности изложения индекс w сохраним: aw. Расстояние между одноименными точками профилей соседних зубьев, измеренное в сечении, нормальном линиям зубьев, называют нормальным шагом р. Отношение р/π называют модулем:
Модуль является основной характеристикой размеров зубьев. Модуль измеряют в мм и назначают из стандартного ряда:... 2; 2,5; 3; 4.... Запишем основные параметры зубчатой передачи через параметры зубчатых колес: – передаточное число с учетом того, что d = mz:
– межосевое расстояние:
Значения aw принимают из ряда предпочтительных чисел Ra 40. Обычно ширина b2 зубчатого колеса меньше ширины шестерни. В расчетах используют отношение ψ ba,которое называют коэффициентом ширины:
Значения ψ ba стандартизованы: 0,1; 0,125; 0,16; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63; 0,8. Для коробок передач с целью уменьшения размеров в направлении осей валов применяют узкие колеса ψ ba = 0,1 – 0,2; для редукторов – широкие колеса: ψ ba = 0,315 – 0,63.
Рисунок 36 – Цилиндрическая передача с внутренним зацеплением Цилиндрические передачи с внутренним зацеплением (рис. 36). В этом случае межосевое расстояние:
Силы в цилиндрическом зубчатом зацеплении. Силы взаимодействия зубьев принято определять в полюсе зацепления. Распределенную по контактной площадке нагрузку q в зацеплении заменяют равнодействующей Fn, нормальной к поверхности зуба.
Рисунок 37 – Силы, действующие в зацеплении Для расчета валов и опор силу Fn удобно представить в виде составляющих (рис. 37): Ft, Fa, Fr. Окружная сила:
Осевая сила:
На ведомом колесе направление окружной силы Ft совпадает с направлением вращения, на ведущем – противоположно ему. Осевая сила параллельна оси колеса. Направление вектора Fa зависит от направления вращения колеса и направления линии зуба. Радиальная сила (см. сечение А–А):
где Т – вращающий момент на зубчатом колесе, Н·м; d – делительный диаметр колеса, мм; β – угол наклона зуба; aw = 20 ° – угол зацепления. Векторы радиальных сил у колес с внешним зацеплением направлены к оси, а у колес с внутренним зацеплением – от оси зубчатого колеса. Особенности геометрии и условий работы косозубых зубчатых передач. Зубья косозубых цилиндрических колес нарезают тем же инструментом, что и прямозубых. Ось червячной фрезы составляет с торцовой плоскостью колеса угол β (рис. 38). При нарезании фрезу перемещают по направлению зубьев колеса. Поэтому в нормальной к направлению зуба плоскости все его размеры – стандартные.
Рисунок 38 – Особенности косозубых колес У пары сопряженных косозубых колес с внешним зацеплением углы β наклона линий зубьев равны, но противоположны по направлению. Если не предъявляют специальных требований, то колеса нарезают с правым направлением зуба, а шестерни — с левым. У косозубого колеса (рис. 38) расстояние между зубьями можно измерить в торцовом, или окружном, (t – t) и нормальном (п – п) направлениях. В первом случае получают окружной шаг р
где т Согласно рис. 38:
Следовательно:
где β – угол наклона зуба на делительном цилиндре. Нормальный модуль должен соответствовать стандарту. В торцовой плоскости t — t косозубое колесо можно рассматривать как прямозубое с модулем т, и углом зацепления
Для колеса без смещения делительный d и начальный dw диаметры
Помимо торцового перекрытия в косозубых передачах обеспечено и осевое перекрытие. Коэффициент осевого перекрытия:
где рх – осевой шаг, равный расстоянию между одноименными точками двух смежных зубьев, измеренному в направлении оси зубчатого колеса (рис. 38). Контактные напряжения при прочих равных условиях в косозубом зацеплении меньше по значению, чем в прямозубом. Понятие об эквивалентном колесе. Как отмечалось, профиль косого зуба в нормальном сечении п – п (рис. 38) совпадает с профилем прямозубого колеса. Расчет косозубых колес ведут, используя параметры эквивалентного прямозубого колеса: т Профиль зуба в этом сечении совпадает с профилем условного прямозубого колеса, называемого эквивалентным, (рис. 39) делительный диаметр dv которого dv = mnzv.
Рисунок 39 – Поперечное сечение косозубого колеса Эквивалентное число зубьев:
С увеличением угла β наклона линии зуба эквивалентные параметры возрастают, способствуя повышению прочности передачи.
|
|||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 784; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.128.236 (0.012 с.) |

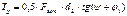 ,
,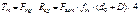 ,
, ,
,
 ,
, ,
, ,
, ,
,
 ,
,
 ,
, ,
, ,
,
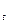 , во втором – нормальный шаг р. Различны в этих направлениях и модули зацепления:
, во втором – нормальный шаг р. Различны в этих направлениях и модули зацепления: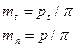 ,
, – окружной и нормальный модули зубьев.
– окружной и нормальный модули зубьев. ,
, ,
,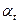 :
: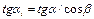 ,
, ,
, ,
,
 , где z – действительное число зубьев косозубого колеса.
, где z – действительное число зубьев косозубого колеса.


