
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конические зубчатые передачи. Основные геометрические соотношения. Эквивалентное колесо. Силы в зацеплении.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
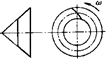
Конические зубчатые передачи передают механическую энергию между валами с пересекающимися осями. Обычно Σ = 90° (рис. 40,а).Зацепление конических зубчатых колес можно рассматривать как качение делительных круговых конусов шестерни и колеса. Основные характеристики: углы делительных конусов δ1 и δ 2, внешнее конусное расстояние Re. Линии пересечения боковых поверхностей зубьев с делительной конической поверхностью называют линиями зубьев. В зависимости от формы линии зуба различают передачи с прямыми зубьями (рис. 40,б), у которых линии зубьев проходят через вершину делительного конуса, и с круговыми зубьями (рис. 40,в), линии зубьев которых являются дугами окружности d0. Конические колеса с круговыми зубьями характеризуют наклоном линии зуба в среднем сечении по ширине зубчатого венца. Угол βn наклона — острый угол между касательной в данной точке к линии зуба и образующей делительного конуса (рис. 40,в). Разновидностью конических передач являются гипоидные передачи, у которых оси вращения зубчатых колес не пересекаются, а перекрещиваются.
Рисунок 40 –Конические зубчатые передачи Геометрия конических зубчатых передач представлена на рис.41.
Рисунок 41 – Геометрия конических зубчатых колес Конические зубчатые передачи необходимо регулировать, добиваясь совпадения вершин делительных конусов колес. Угол Σ между осями зубчатых колес равен сумме углов делительных конусов (рис. 18.1):
Достоинство конических передач – возможность передачи механической энергии между валами с пересекающимися осями. Недостатками являются необходимость регулирования передачи (вершины делительных конусов должны совпадать), а также меньшая нагрузочная способность и большая сложность изготовления по сравнению с цилиндрическими передачами. Внешние и внутренние торцы на конических зубчатых колесах формируют внешними и внутренними дополнительными конусами, образующие которых перпендикулярны образующей делительного конуса. Средний дополнительный конус расположен на равном расстоянии от внешнего и внутреннего дополнительных конусов. Ширина b венца зубчатого колеса ограничена двумя дополнительными конусами – внешним и внутренним. Длину отрезка образующей делительного конуса от его вершины до внешнего торца называют внешним конусным расстоянием Re, до середины ширины зубчатого венца – средним конусным расстоянием Rm (рис. 41).
Пересечения делительных конусов с дополнительными конусами определяют диаметры делительных окружностей конического зубчатого колеса. Различают внешний de, внутренний d Основные геометрические соотношения. В конических зубчатых колесах с осевыми формами I и II высота зуба, а следовательно, и модуль зацепления увеличиваются от внутреннего к внешнему дополнительному конусу (рис. 41, 42). Для удобства измерения размеры конических колес принято определять по внешнему торцу зуба. Максимальный модуль зубьев – внешний окружной модуль тte – получают на внешнем торце колеса. Ниже приведены основные геометрические соотношения для конических зубчатых передач (рис. 41). Внешнее конусное расстояние:
Внешние делительные диаметры шестерни и колеса:
Ширина зубчатого венца:
Для большинства конических передач коэффициент ширины зубчатого венца Тогда:
Среднее конусное расстояние:
Из условия подобия (рис. 18.1) следует:
Тогда средний делительный диаметр шестерни:
Модуль окружной в среднем сечении:
Модуль нормальный в среднем сечении для кругового зуба (
Углы делительных конусов:
Рисунок 43 – Эквивалентное колесо Для конических зубчатых колес с прямыми зубьями в качестве расчетного принимают внешний окружной модуль mte, для конических зубчатых колес с круговыми зубьями – средний нормальный модуль тп в середине зубчатого венца. Эквивалентное колесо. Для прямозубой передачи профили зубьев конического колеса на среднем дополнительном конусе (рис. 43) близки к профилям зубьев цилиндрического прямозубого колеса с делительным диаметром dv. Дополнив развертку среднего дополнительного конуса на плоскость (рис. 44) до полной окружности, получим эквивалентное цилиндрическое колесо с числом зубьев
Рисунок 44 – Развертка среднего дополнительного конуса на плоскость Эквивалентного числа зубьев:
т.е. фактическое коническое прямозубое колесо с числом зубьев z в прочностных расчетах можно заменить цилиндрическим с числом зубьев zv.
Для передачи с круговыми зубьями профили зубьев конического колеса в нормальном сечении близки к профилям зубьев эквивалентного цилиндрического прямозубого колеса. Эквивалентное число зубьев zvn получают двойным приведением: конического колеса к цилиндрическому и кругового зуба к прямому зубу:
Силы в коническом зубчатом зацеплении. В конической передаче местом приложения силы F Окружная сила F
где Т dm В прямозубой передаче (рис. 45) для определения составляющих запишем промежуточное выражение (αw = 20° – угол зацепления)
Радиальная сила на шестерне:
Осевая сила на шестерне:
Рисунок 45 – Силы, действующие в зацеплении Силы на колесе соответственно равны (рис. 46):
Рисунок 46 – Осевые и радиальные силы В передаче с круговым зубом во избежание заклинивания зубьев при значительных зазорах в подшипниках необходимо обеспечить направление осевой силы Fa1 на ведущей шестерне к основанию делительного конуса. Для этого направление вращения ведущей шестерни (если смотреть со стороны вершины делительного конуса) и направление наклона зубьев должны совпадать. По рис. 47 шестерня вращается против хода часовой стрелки, т.е. влево, и зуб шестерни левый.
Рисунок 47 – Направление зуба шестерни В передаче с круговым зубом при соблюдении этого условия: радиальная сила на шестерне:
осевая сила на шестерне:
Такие же знаки в формулах будут при вращении по ходу часовой стрелки ведущей шестерни с правым зубом. Силы на колесе соответственно равны: Fr2 = Fal; Fa2 = Frl.
|
||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.81.40 (0.009 с.) |



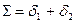 , (61)
, (61) , средний dm делительные диаметры.
, средний dm делительные диаметры. ,
, ,
, ,
,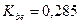 .
. ,
, ,
, ,
, ,
, ,
, =35°):
=35°): ,
, ,
,
 и делительным диаметром:
и делительным диаметром: ,
,
 ,
, ,
, действующей перпендикулярно поверхности зуба, считают сечение на середине ширины зубчатого венца. Для расчета валов и опор силу Fn удобно представить в виде составляющих: Ft, Fr и Fa.
действующей перпендикулярно поверхности зуба, считают сечение на середине ширины зубчатого венца. Для расчета валов и опор силу Fn удобно представить в виде составляющих: Ft, Fr и Fa. (H) на шестерне:
(H) на шестерне: ,
, – вращающий момент, Н·м;
– вращающий момент, Н·м; ,
,
 ,
,
 ,
,
 ,
, ,
,


