
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет геометрии конических зубчатых передач. Особенности расчета передач с круговым зубом.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Формула для проверочного расчета конических прямозубых колес на контактную прочность:
При расчете по среднему конусному расстоянию R = Re - 0,5b формула (3.27) принимает вид:
Здесь Re и R- внешнее и среднее конусные расстояния, мм; Аналогичный расчет для конических колес с круговыми зубьями основывается на формулах (3.4) и (3.6). Рекомендуют принимать средний угол наклона зуба
Коэффициент нагрузки Кн представляет собой произведение трех частных коэффициентов, определяемых так же, как и для цилиндрических косозубых колес:
При проектировочном расчете определяют внешний делительный диаметр колеса, мм:
Далее определяют числа зубьев колес. Для шестерни
Рекомендуют выбирать Число зубьев колеса z2 =
Особенности расчета конических колес с круговыми зубьями
Расчетные формулы для рассматриваемых колес приводятся по аналогии с формулами для цилиндрических косозубых колес. Наименования и обозначения геометрических параметров даны по ГОСТ 19326-73. Рекомендуется принимать средний угол наклона зуба Окружное усилие
Коэффициент формы зубьев надо выбирать по биэквивалентному числу зубьев
Червячные передачи. Достоинства и недостатки. Основные геометрические параметры и кинематика. Смещение в червячной передаче. Передаточное отношение. Скольжение в червячной передаче. Точность изготовления и регулировка. Червячные передачи применяют для передачи вращательного движения между валами, у которых угол скрещивания осей обычно составляет 0 = 90°. В большинстве случаев ведущим является червяк, т. е. короткий винт с трапецеидальной или близкой к ней резьбой. Для облегания тела червяка венец червячного колеса имеет зубья дугообразной формы, что увеличивает длину контактных линий в зоне зацепления. Червячная передача — это зубчато-винтовая передача, движение в которой осуществляется по принципу винтовой пары.
Червяк 1 – это винт с трапецеидальной или близкой к ней по форме резьбой. Червячное колесо является косозубым зубчатым колесо с зубьями особой дуговой формы. Такая форма зубьев обеспечивает увеличение их длины и прочности зубьев на изгиб. Червячные передачи применяют при необходимости передачи движения между перекрещивающимися (как правило, взаимно перпендикулярными) валами. При вращении червяка его витки плавно входят в зацепление с зубьями колеса и приводят его во вращение. Передачи используют в станках, автомобилях, подъемно-транспортных и других машинах. Достоинства и недостатки Достоинства: Плавность работы; Бесшумность; Большое передаточное отношение в одной паре, благодаря чему червячные редукторы с большим передаточным числом значительно более компактны и менее массивны, чем эквивалентные зубчатые; Самоторможение; Повышенная кинематическая точность. Недостатки: Сравнительно низкий КПД (целесообразно применять при мощностях менее 100 кВт); Большие потери на трение (тепловыделение); Повышенный износ и склонность к заеданию; Повышенные требования к точности сборки, необходимость регулировки; Необходимость специальных мер по интенсификации теплоотвода; Передача вращения возможна только в одном направлении (от винта к колесу). Расчет червячных передач Передаточное число червячной передачи определяется по формуле
где u - соответственно частота вращения червяка и червячного колеса; z2= 28 — 80 — число зубьев червячного колеса; z1= 1; 2; 4 — число заходов червяка.
Минимальное число зубьев червячного колеса для силовых передач принимают из условия отсутствия подрезания зубьев, для некорригированной передачи z2 >- 28. При z2> 80 происходит уменьшение модуля и ширины червячного колеса, что в свою очередь приводит к ослаблению червячной передачи. Число заходов червяка z1 выбирают в зависимости от передаточного числа. По ГОСТ 2144—66 стандартизованы червяки: одно-, двух- и четырехзаходные. Мощные передачи не выполняют однозаходными из-за малого кпд и сильного нагрева. Для силовых передач u = 7 — 80, для приборов до 500 и более. Геометрические параметры червячной передачи без коррекции определяют по следующим формулам:
где
р — делительный осевой шаг витков червяка. Для закрытых передач с цилиндрическим червяком коэффициент диаметра червяка выбирают в пределах q=7,5—16, меньшее значение принимают для быстроходных передач.
где ha и hf — соответственно высота делительной головки витка и высота делительной ножки витка червяка (для некорригированной передачи ha= m и hf = 1,2 m). Длина нарезной части червяка: при при Делительное межосевое расстояние - расчетный модуль -
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.184.36 (0.007 с.) |

 (3.27)
(3.27)
 – коэффициент нагрузки,
– коэффициент нагрузки,  - вращающий момент на колесе, Н*мм;
- вращающий момент на колесе, Н*мм;  -ширина зубчатого венца, мм.
-ширина зубчатого венца, мм. = 35°. При этом коэффициент, учитывающий формулу сопряженных поверхностей зубьев, ZH = 1,59. Коэффициент ZƐ можно принять таким же, как и для цилиндрических косозубых колес, т.е. ZƐ = 0,8. Тогда для проверочного расчета стальных конических колес с круговыми зубьями на контактную прочность формула будет иметь вид:
= 35°. При этом коэффициент, учитывающий формулу сопряженных поверхностей зубьев, ZH = 1,59. Коэффициент ZƐ можно принять таким же, как и для цилиндрических косозубых колес, т.е. ZƐ = 0,8. Тогда для проверочного расчета стальных конических колес с круговыми зубьями на контактную прочность формула будет иметь вид:

 (3.29)
(3.29) (3.30)
(3.30)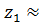 18÷32.
18÷32. . Так как найденные значения
. Так как найденные значения  и
и  округляют до целых чисел, то после этого следует уточнить u =
округляют до целых чисел, то после этого следует уточнить u =  и угол
и угол  . Внешний окружной модуль
. Внешний окружной модуль 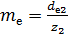 ; округлять полученное значение mе не обязательно.
; округлять полученное значение mе не обязательно.

 Для расчета конических колес с круговыми зубьями (см. рис. 3.5) их заменяют эквивалентными цилиндрическими прямозубыми колесами.
Для расчета конических колес с круговыми зубьями (см. рис. 3.5) их заменяют эквивалентными цилиндрическими прямозубыми колесами. .
. , где
, где  – средний нормальный модуль зубьев.
– средний нормальный модуль зубьев.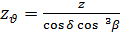 .
. Червячные передачи – это передачи зацеплением с непосредственным контактом витков червяка и зубьев червячного колеса (рис).
Червячные передачи – это передачи зацеплением с непосредственным контактом витков червяка и зубьев червячного колеса (рис). , (4.43)
, (4.43) — соответственно угловые скорости червяка и червячного колеса;
— соответственно угловые скорости червяка и червячного колеса; ;- делительный диаметр червяка
;- делительный диаметр червяка ,- начальный диаметр червяка,
,- начальный диаметр червяка,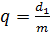 - коэффициент диаметра червяка;
- коэффициент диаметра червяка; -расчетный модуль червяка;
-расчетный модуль червяка; , - диаметр вершин витков червяка
, - диаметр вершин витков червяка , - диаметр впадин червяка,
, - диаметр впадин червяка, ,
,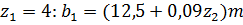 .
.
 .
.


