
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зубчатые передачи. Силы зацепления косозубой зубчатой передачи. Критерии работоспособности и расчета зубчатых передачСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Зубчатые передачи называются трехзвенным механизмом, в котором 2 подвижных звена являются зубчатыми колесами, образующими с неподвижным звеном вращательную или поступательную пару. Зубчатая передача состоит из 2 колес или колеса и рейки с зубьями, посредством которых они сцепляются между собой. Зубчатое колесо с меньшим числом зубьев называется шестерней, с большим – колесом. По форме колеса зубчатые передачи: цилиндрические, конические. эллиптические, фигурные зубчатые колеса, колеса с неполным числом зубьев. По форме и расположению зубьев: прямые, косые, шевронные, круговые. В зависимости от относительного расположения зубчатых колес передачи могут быть с внешним или внутренним зацеплением.
Окружная: Ft=2T/d Радиальная: Fr=Fttga/cosb Осевая: Fa=Fttgb
Закрытые зубчатые передачи рассчитывают на выносливость по контактным напряжениям во избежание усталостного выкрашивания рабочих поверхностей зубьев. Затем выполняют проверочный расчет на выносливость зубьев по напряжениям изгиба для предотвращения усталостного разрушения зубьев. Открытые зубчатые передачи рассчитывают на выносливость по напряжениям изгиба с учетом износа зубьев в процессе эксплуатации. В этом случае нет необходимости проверять выносливость поверхностей зубьев по контактным напряжениям, т к абразивный износ поверхностей зубьев предотвращает выкрашивание их от переменных контактных напряжений. Зубчатые передачи, работающие с большими кратковременными (пиковыми) перегрузками, необходимо проверять на отсутствие опасности хрупкого разрушения или пластических деформаций рабочих поверхностей зубьев от контактных напряжений, а также на отсутствие хрупкого излома или пластических деформаций при изгибе. Это относится как к закрытым, так и к открытым передачам.
Расчет цилиндрических зубчатых передач на контактную выносливость. Приведенный радиус кривизны и расчетные контактные напряжения в полюсе зацепления. σН0 – контактное напряжение в полюсе зацепления:σН0=ZEZHZε ZE – коэф-т,учитывающий механические свойства материалов сопряженных зубчатых колес ZH – коэф-т, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления: ZH= at - делительный угол профиля в торцевом сечении: tgat=tga/cosb bt - основной угол наклона для косозубой передачи: sinbt =sinb cosa Zε – коэф-т. учитывающий суммарную длину контактных линий. Зависит от осевого коэф-та перекрытия εb Ft – окружная сила, u – передаточное отношение, d – диаметр колеса, b – ширина колеса. Приведенный радиус кривизны цилиндров: rпр=r1 r2/r1 +r2 , где r1 r2 – радиусы цилиндров. Радиус кривизны профиля зуба в полюсе зацепления: r=1/2 dw sin atw (для прямозубых колес) Расчетные контактные напряжения в полюсе зацепления. Формула для расчета активных поверхностей зубьев на контактную выносливость Расчетное контактное напряжение: σН= σН0√КН Где σН0 – контактное напряжение в полюсе зацепления:σН0=ZEZHZε ZE – коэф-т,учитывающий механические свойства материалов сопряженных зубчатых колес ZH – коэф-т, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления: ZH= at - делительный угол профиля в торцевом сечении: tgat=tga/cosb bt - основной угол наклона для косозубой передачи: sinbt =sinb cosa Zε – коэф-т. учитывающий суммарную длину контактных линий. Зависит от осевого коэф-та перекрытия εb Ft – окружная сила, u – передаточное отношение, d – диаметр колеса, b – ширина колеса. КН – коэф-т нагрузки:КН=КAКHVКHbКHa Где КA – коэф-т, учитывающий внешнюю динамическую нагрузку КHV – коэф-т, учитывающий внутреннюю динамическую нагрузку, возникающую в зацеплении до зоны резонанса: КHV=1+(ωHV b/Ft КA) ωHV – окружная динамическая сила: ωHV=dН g0 V dН – коэф-т, учитывающий влияние вида зубчатой передачи и модификации профиля головок зубьев g0 – коэф-т, учитывающий влияние разности шагов зацепления зубьев, шестерни и колеса V – скорость в зацеплении КHb - коэф-т неравномерности распределения нагрузки по длине контактных линий КHa - коэф-т, учитывающий распределение нагрузки между зубьями
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 793; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.119.143 (0.008 с.) |

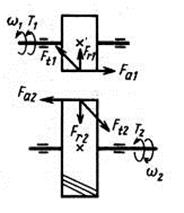 Силы зацепления:
Силы зацепления:





