
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные геометрические параметры прямозубой цилиндрической эвольвентой передачи. Основная теорема зубчатого зацепления. Эвольвента окружности и ее свойства.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Основные параметры эвольвентных прямозубых цилиндрических передач. Длина делительной окружности зубчатого колеса Диаметр основной окружности при профильном угле исходного контура Диаметр окружности вершин зубьев: Диаметр окружности их впадин: толщина зуба по делительной окружности, равная ширине впадины рейки по начальной прямой, Теорема зацепления. Постоянное передаточное отношение при вращении зубчатых колес достигается за счет придания профилю зубьев определенной формы. В основу докозательства постоянства передат. отнош. соприкасающихся профилей пары зубьев в течение всего времени контакта положена теорема зацепления. Два касающихся в точке М зуба(рис. 18,2) вращаются с угловыми скоростями ведущего Таким образом, основная теорема зацепления заключается в след.: общая нормаль, проведенная к сопряженным профилям зубьев, делит межосевое расстояние (
Окружность по котор. перекатыв. прямая при образовании эвольвенты наз. основн. окружн., а прямая образующ. прямой. Окружность, по которой перекатывается прямая при образовании эвольвенты, назыв. основной окружностью, а прямая - образующей прямой. Основные свойства эвольвенты окружности явл. то, что образующ. прямая всегда перпендикулярна к эвольвенте, следует что отрезки 1"А 2"А - хорды, явл. мгновенными радиусами кривизны эвольвенты. Эвольвента начин. на основной окружности и всегда расположена вне ее, та кривая бес перегибов и ее форма зависит только от радиуса основной окружности. т.к точка М прямой МК (рис. 18,5) явл. мгновенным центром вращ. отрезок КМ будет радиусом кривизны. Эвольвенты в точке К. Координаты К эвольвенты r - радиус вектор. Свойства эвольвенты:
Основные геометрические параметры косозубой цилиндрической эвольвентой передачи. Силы зацепления. Расчет на прочность. Геометрические параметры
Межосевое расстояние Силы зацепления В зацеплении косозубых колес (рис.18.15) сила окружную силу нормальная сила Возникновение осевой силы в зацеплении является недостатком косозубых передач, т.к. эта сила создает на валу сосредоточенный изгибающий момент и дополнительно нагружает подшипник. Расчетная нагрузка. Расчет зубьев на прочность ведут по удельной расчетной нагрузке q, которая представляет собой отношение нормальной силы к суммарной длине контактных линий
Суммарная длина контактных линий зависит от ширины венца колеса
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 805; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

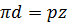 а диаметр
а диаметр 
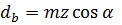
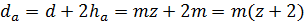

 , где x-смещение инструмента.
, где x-смещение инструмента.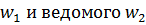 колес, причем зуб ведущего колеса давит на зуб ведомого колеса. Скорость в точке касания
колес, причем зуб ведущего колеса давит на зуб ведомого колеса. Скорость в точке касания  . Проведем через точку Ь общую нормаль N-N и общую касательную T-T. На эти направления разложим векторы
. Проведем через точку Ь общую нормаль N-N и общую касательную T-T. На эти направления разложим векторы 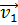 и
и  . Т.к. треугольники
. Т.к. треугольники 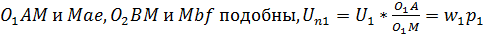 ,
,  где
где  ,
, 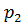 - длина перпендикуляров к общей нормали N-N, проведены из центров вращения
- длина перпендикуляров к общей нормали N-N, проведены из центров вращения  и
и 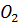 . Если
. Если 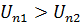 , то зуб ведущего колеса будет врезаться в зуб ведомого колеса. При
, то зуб ведущего колеса будет врезаться в зуб ведомого колеса. При 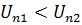 , зуб ведомого колеса будет опережать зуб ведущего, в результате чего нарушится непрерывность их контакта. Следовательно, для нормальной работы передачи необходимо выполнение условия
, зуб ведомого колеса будет опережать зуб ведущего, в результате чего нарушится непрерывность их контакта. Следовательно, для нормальной работы передачи необходимо выполнение условия  . Из подобия треугольников
. Из подобия треугольников 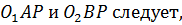 что
что 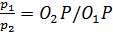 . Т.к. положение точки P, называемой полюсом зацепления, одно и то же в любом моменте зацепления, передаточное отношение должно быть постоянным:
. Т.к. положение точки P, называемой полюсом зацепления, одно и то же в любом моменте зацепления, передаточное отношение должно быть постоянным: 
 на отрезки(
на отрезки(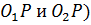 , длина которых обратно пропорциональна угловой скорости колес. Эвольвентой окружности называют кривую, описываемую точкой прямой линии, перекатывающейся по окружности без скольжения. При перекатыв. прямой по окружности(рис. 18,4) точка 1 прямой будет в точке 1" окружности, тогда 2 в точке 2" окружности и т.д. В точках 1", 2",3"... проведем касательные к окружности перпендикулярно к ее радиусу. На касат. положим отрезки
, длина которых обратно пропорциональна угловой скорости колес. Эвольвентой окружности называют кривую, описываемую точкой прямой линии, перекатывающейся по окружности без скольжения. При перекатыв. прямой по окружности(рис. 18,4) точка 1 прямой будет в точке 1" окружности, тогда 2 в точке 2" окружности и т.д. В точках 1", 2",3"... проведем касательные к окружности перпендикулярно к ее радиусу. На касат. положим отрезки 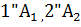 равные соотв. отрезкам прямой 1А и 2А и тд. Соединив точки
равные соотв. отрезкам прямой 1А и 2А и тд. Соединив точки  и тд. плавной кривой, получим эвольвенту окружности.
и тд. плавной кривой, получим эвольвенту окружности.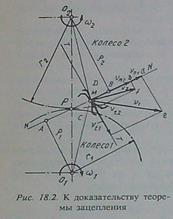


 - угол отклонения рад вектора от начала эвольвенты. Если
- угол отклонения рад вектора от начала эвольвенты. Если  угол м/д отрезками ОМ и ОК, то
угол м/д отрезками ОМ и ОК, то 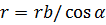

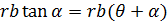

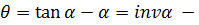 уре. эвольвенты.
уре. эвольвенты. 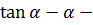 инвалюта (см. в табл.)
инвалюта (см. в табл.)
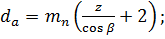
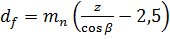

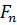 составляющие:
составляющие: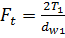 ; осевую
; осевую  ; радиальную силу
; радиальную силу 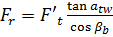
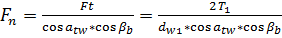 При
При 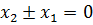

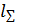 , с учетом коэффициента
, с учетом коэффициента 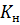 , отражающего влияние на работу зубчатой передачи различных факторов;
, отражающего влияние на работу зубчатой передачи различных факторов;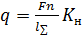
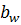 . Значение
. Значение  не остается постоянным, так как в передаче нагрузки могут участвовать от одной до нескольких пар контактирующих зубьев. Минимальное значение
не остается постоянным, так как в передаче нагрузки могут участвовать от одной до нескольких пар контактирующих зубьев. Минимальное значение 


