
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эвольвента окружности, построение и свойстваСодержание книги
Поиск на нашем сайте
Можно указать следующий способ образования эвольвенты. Выбирается основная окружность rb , касающаяся ее производящая прямая и чертящая точка на ней. Перекатывая производящую прямую по окружности без скольжения, получаем траекторию чертящей точки, которая является эвольвентой, т.к. мгновенные радиусы кривизны ее лежат на основной окружности. Эвольвенту можно получить, наматывая нить с чертящей точкой на диск (рис. 5.5). Две чертящие точки дадут две эквидистантные (равноотстоящие) эвольвенты. Приближенное графическое построение эвольвенты как кривой, составленной из множества дуг окружностей, представлено на рис.5.5 б. Из определения эвольвенты и из указанных выше способов ее построения вытекают следующие очевидные свойства: 1. Нормаль эвольвенты касается основной окружности. 2. Радиус кривизны эвольвенты равен длине нормали. 3. Длина нормали эвольвенты равна длине соответствующей дуги основной окружности 4. Расстояние между эквидистантными эвольвентами равно длине соответствующей дуги основной окружности УРАВНЕНИЕ ЭВОЛЬВЕНТЫ В ПОЛЯРНЫХ КООРДИНАТАХ Наиболее удобная форма записи уравнения эвольвенты – в полярных координатах в параметрической форме. В качестве параметра принимается угол профиля эвольвенты. Углом профиля эвольвенты αy называется угол между направлением радиус–вектора к текущей точке Y и направлением касательной Т – Т. Он изменяется в пределах 0 - 90˚, практически используется участок эвольвенты, где αy = 0 - 30˚.
Проведем из точки Y нормаль N –N, которая по 1-му свойству эвольвенты коснется основной окружности в точке В. Заметим, что угол BOY равен углу профиля эвольвенты в данной точке. Из треугольника OBY следует ry = rb / cos αy Введем угол νy , тогда νy = αy + θy, откуда следует θy = νy - αy.
Из построений на рис. 5.6 и в силу 3-го свойства эвольвенты длина дуги ВА0 равна BY. Из треугольника BYO следует BY/rb = tg αy . На основании приведенных зависимостей нетрудно установить, что центральный угол νy = tg αy. Функция θy = tg αy - αy получила название эвольвентной функции или инволюты. Иногда используется условное обозначение θy = - inv αy. ЭВОЛЬВЕНТНОЕ ЗАЦЕПЛЕНИЕ
Введем две окружности, проходящие через полюс зацепления. Такие окружности называются начальными. Они перекатываются друг по другу без скольжения и служат центроидами зубчатых колес. Эвольвентное зацепление получило широкое распространение благодаря ряду достоинств: 1. Эвольвентное зацепление нечувствительно к небольшому изменению межосевого расстояния, что удешевляет изготовление корпусных деталей. 2. Для нарезания эвольвентных зубчатых колес можно применять простой инструмент с прямолинейной режущей кромкой. 3. При изготовлении колес путем простого смещения инструмента можно добиваться новых положительных свойств. ИЗГОТОВЛЕНИЕ ЗУБЧАТЫХ КОЛЕС Существуют два способа изготовления зубчатых колес: способ копирования и способ обкатки. Способом копирования дисковой или пальцевой фрезой на обычном фрезерном станке вырезается впадина между зубьями (рис.5.7) Поскольку в зависимости от числа зубьев размеры впадины при одном и том же модуле изменяются, нужно иметь очень много фрез. На практике одной фрезой нарезаются колеса в некотором диапазоне чисел зубьев, указанном на фрезе, что не очень точно. Неточность может быть исправлена последующей шлифовкой.
Способ копирования недостаточно производителен, т.к. в работе находится один зуб, много времени тратится на перестановку заготовки. Поэтому способ применяется в единичном и мелкосерийном производстве, при нарезании неответственных, тихоходных колес.
Способ обкатки получил наибольшее распространение. Он производителен, т.к. обрабатывается несколько зубьев сразу, процесс зубонарезания идет непрерывно. Профиль зуба формируется с учетом числа зубьев колеса, поэтому нарезание точное. По такому же принципу производится чистовая обработка, шлифование зубьев. ИСХОДНЫЙ КОНТУР Из описания способов изготовления зубчатых колес ясно, что размеры зуба полностью зависят от профиля инструмента. По ГОСТ профиль инструмента стандартизован путем задания так называемого «исходного контура». На рис.5.9 представлен теоретический исходный контур. Он выполнен в виде рейки с трапециевидными зубьями.
Шаг рейки p - расстояние между одноименными точками двух соседних зубьев. Шаг складывается из толщины зуба s и ширины впадины e. Та единственная прямая, на которой толщина зуба равна ширине впадины, называется делительной прямой рейки., остальные прямые называются начальными. Шаг зубьев рейки p = π m s = e = π m / 2. Делительная прямая делит зуб на головку и ножку. Высота головки – ha = 1.25 m, высота ножки – hf = m, высота всего зуба – h = 2.25 m. Головка закруглена радиусом ρ = 0.38 m. Инструмент изготавливается по производящему исходному контуру, отличающемуся от теоретического исходного контура тем, что впадина сделана глубже на 0.25 m и закруглена так же как головка. Это сделано для того, чтобы впадина инструмента не касалась заготовки. Следовательно, впадина не участвует в нарезании зуба. Зуб нарезают прямолинейные боковые кромки и скругленная вершина зуба. Рейку можно рассматривать как зубчатое колесо бесконечно большого радиуса. В этом случае эвольвента превращается в прямую линию.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1542; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.10.195 (0.006 с.) |

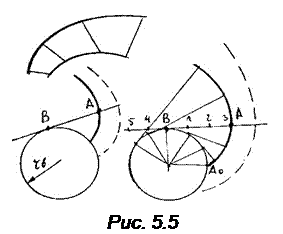 Геометрическое место центров кривизны какой-либо кривой называют инволютой, а саму кривую – эвольвентой (рис. 5.5). При профилировании зубьев в качестве эволюты используется окружность, называемая в дальнейшем основной, а сам зуб очерчивается эвольвентой окружности. Единственным параметром, отличающим одну эвольвенту от другой, является радиус основной окружности.
Геометрическое место центров кривизны какой-либо кривой называют инволютой, а саму кривую – эвольвентой (рис. 5.5). При профилировании зубьев в качестве эволюты используется окружность, называемая в дальнейшем основной, а сам зуб очерчивается эвольвентой окружности. Единственным параметром, отличающим одну эвольвенту от другой, является радиус основной окружности. Полярные координаты ry и θy укажут положение точки Y. Установим зависимость ry и θy от параметра αy .
Полярные координаты ry и θy укажут положение точки Y. Установим зависимость ry и θy от параметра αy .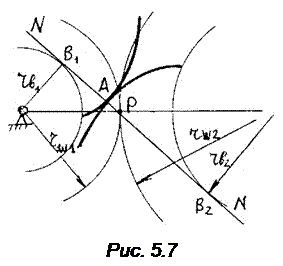 На рис. 5.7 представлено зацепление эвольвентных профилей. Общая нормаль N – N. Проведенная через точку касания двух профилей, обязана согласно 1-му свойству эвольвенты, коснуться основных окружностей. Поскольку таких окружностей две, положение нормали единственно и неизменно. Тем самым подтверждается выполнение следствия основного закона зацепления. В процессе зацепления точка касания профилей не может сойти с общей нормали N – N, т.к. в противном случае нарушилось бы 1-ое свойство. Установлено, что при эвольвентном зацеплении профилей точка касания движется по общей нормали с постоянной скоростью.
На рис. 5.7 представлено зацепление эвольвентных профилей. Общая нормаль N – N. Проведенная через точку касания двух профилей, обязана согласно 1-му свойству эвольвенты, коснуться основных окружностей. Поскольку таких окружностей две, положение нормали единственно и неизменно. Тем самым подтверждается выполнение следствия основного закона зацепления. В процессе зацепления точка касания профилей не может сойти с общей нормали N – N, т.к. в противном случае нарушилось бы 1-ое свойство. Установлено, что при эвольвентном зацеплении профилей точка касания движется по общей нормали с постоянной скоростью. При способе обкатки инструмент и заготовка совершают относительное движение обкатывания, инструмент своими режущими кромками постепенно внедряется в заготовку, прокладывая себе путь. Таким образом, возникает станочное зацепление, аналогичное обычному зацеплению с той разницей, что одно из звеньев является инструментом. Инструмент выполняется в виде гребенки, червячной фрезы или долбяка. Этот способ требует применения специальных зубофрезерных станков. В одних конструкциях станков инструмент обкатывается вокруг неподвижной заготовки, в других – инструмент движется поступательно, заготовка поворачивается, в третьих – заготовка и инструмент (долбяк) вращаются (рис.5.8).
При способе обкатки инструмент и заготовка совершают относительное движение обкатывания, инструмент своими режущими кромками постепенно внедряется в заготовку, прокладывая себе путь. Таким образом, возникает станочное зацепление, аналогичное обычному зацеплению с той разницей, что одно из звеньев является инструментом. Инструмент выполняется в виде гребенки, червячной фрезы или долбяка. Этот способ требует применения специальных зубофрезерных станков. В одних конструкциях станков инструмент обкатывается вокруг неподвижной заготовки, в других – инструмент движется поступательно, заготовка поворачивается, в третьих – заготовка и инструмент (долбяк) вращаются (рис.5.8). Размеры рейки выражаются через один основной параметр, называемый модулем. Модуль m имеет размерность мм и выбирается из ряда рациональных чисел от 0.05 до 100.
Размеры рейки выражаются через один основной параметр, называемый модулем. Модуль m имеет размерность мм и выбирается из ряда рациональных чисел от 0.05 до 100.


