
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация зубчатых механизмовСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте КЛАССИФИКАЦИЯ ЗУБЧАТЫХ МЕХАНИЗМОВ Зубчатые механизмы – это самый распространенный и, пожалуй, самый важный вид механизмов. Трудно найти такую машину, в которой нет зубчатого механизма. Они применяются в станках, в грузоподъемных машинах, автомобилях, разнообразных технологических машинах и т.д. Основные достоинства зубчатых механизмов, определившие их широкое применение, - строго постоянное передаточное отношение, большая передаваемая мощность на единицу массы, компактность, долговечность, высокий к.п.д. Недостаток – сложность изготовления и высокая стоимость.
Чтобы устранить отмеченные недостатки, диски снабжаются чередующимися выступами и впадинами, располагающимися с определенным интервалом. Такие выступы называются зубьями. Зубчатым колесом называется звено с замкнутой системой зубьев, обеспечивающей непрерывность движения. Различают еще зубчатый сектор, зубчатую рейку. Зубчатая передача – трехзвенный механизм, состоящий из двух колес и стойки. Важнейшей характеристикой зубчатой передачи является передаточное отношение – отношение угловых скоростей колес. Две или более зубчатые передачи образуют зубчатый механизм. Зубчатые колеса, зубчатые передачи и зубчатые механизмы чрезвычайно разнообразны. Поэтому целесообразно ознакомиться с их простейшей классификацией. Зубчатые колеса бывают: а) цилиндрические и конические, б) прямозубые, винтовые, шевронные, в) эвольвентные, циклоидальные, цевочные, трохоидальные, круговинтовые, г) с внешним и с внутренним зацеплением. Винтовые колеса могут быть с левым и с правым наклоном зуба. Винтовые колеса с винтовой линией постоянного шага называют косозубыми. Зубчатые передачи бывают: а) с постоянным и переменным передаточным отношением некруглые колеса), б) плоские и пространственные, в) с параллельными, пересекающимися и скрещивающимися осями колес. По этому признаку различают цилиндрические, конические, гиперболоидные передачи.
ОСНОВНОЙ ЗАКОН ЗАЦЕПЛЕНИЯ Простейшие зубчатые механизмы применялись еще в древнейшие времена, например, для передачи движения с водяного колеса на жернов. Профиль зубьев мог быть любым, выдерживался только постоянный шаг. Увеличение быстроходности передачи потребовало соответствующего профилирования зубьев. При случайном выборе профиля зубьев мгновенное передаточное отношение переменно, что недопустимо, т. к. колебания скорости выходного звена вызывают инерционные нагрузки, удары в передаче. Профиль зубьев должен быть таким, чтобы угловая скорость выходного звена была строго постоянной. Чтобы ответить на вопрос, каким должен быть профиль, вначале познакомимся с основным законом зацепления. Нормаль, проведенная через точку касания двух профилей, делит межосевое расстояние на части, обратно пропорциональные угловым скоростям этих профилей. Требуется доказать, что O1P / O2 P =ω2 / ω1 (рис.5.4)
Через точку А проведем нормаль N – N и касательную Т – Т и разложим скорости точек А1 и А2 на эти направления. Заметим, что v1 = ω1 r1, v2 = ω2 r2. Кроме того, v1n = v2n - из условия отсутствия вдавливания профилей или их размыкания. Тангенциальные составляющие v1τ ≠ v2τ, что обусловливает скольжение профилей. Из подобия треугольников AV1V1n и O1B1A следует: V1n/V1 = rb1 / r1 откуда V1n = ω1 rb1. Из подобия треугольников AV2V2n и O2B2A следует: V2n / V2 = rb2 / r2 откуда V2n = ω2 rb2. Учитывая, что V1n = V2n, получим ω1 rb1 = ω2 rb2. Из подобия треугольников O1B1P и O2B2P следует rb1 / rb2 = O1P / O2P. С учетом записанных выше соотношений получим ω1 / ω2 = O2P / O1P, что и требовалось доказать. Следствие основного закона зацепления: для постоянства передаточного отношения необходимо, чтобы нормаль, проведенная через точку касания двух профилей, пересекала межосевую линию в постоянной точке (полюсе зацепления). Иными словами требуется неизменность положения полюса. В качестве профилей зубьев могут использоваться кривые, для которых выполняется указанное требование, Такие кривые называются сопряженными. К ним, в частности, относится эвольвента окружности. ЭВОЛЬВЕНТНОЕ ЗАЦЕПЛЕНИЕ
Введем две окружности, проходящие через полюс зацепления. Такие окружности называются начальными. Они перекатываются друг по другу без скольжения и служат центроидами зубчатых колес. Эвольвентное зацепление получило широкое распространение благодаря ряду достоинств: 1. Эвольвентное зацепление нечувствительно к небольшому изменению межосевого расстояния, что удешевляет изготовление корпусных деталей. 2. Для нарезания эвольвентных зубчатых колес можно применять простой инструмент с прямолинейной режущей кромкой. 3. При изготовлении колес путем простого смещения инструмента можно добиваться новых положительных свойств. ИЗГОТОВЛЕНИЕ ЗУБЧАТЫХ КОЛЕС Существуют два способа изготовления зубчатых колес: способ копирования и способ обкатки. Способом копирования дисковой или пальцевой фрезой на обычном фрезерном станке вырезается впадина между зубьями (рис.5.7) Поскольку в зависимости от числа зубьев размеры впадины при одном и том же модуле изменяются, нужно иметь очень много фрез. На практике одной фрезой нарезаются колеса в некотором диапазоне чисел зубьев, указанном на фрезе, что не очень точно. Неточность может быть исправлена последующей шлифовкой. Способ копирования недостаточно производителен, т.к. в работе находится один зуб, много времени тратится на перестановку заготовки. Поэтому способ применяется в единичном и мелкосерийном производстве, при нарезании неответственных, тихоходных колес.
Способ обкатки получил наибольшее распространение. Он производителен, т.к. обрабатывается несколько зубьев сразу, процесс зубонарезания идет непрерывно. Профиль зуба формируется с учетом числа зубьев колеса, поэтому нарезание точное. По такому же принципу производится чистовая обработка, шлифование зубьев. ИСХОДНЫЙ КОНТУР Из описания способов изготовления зубчатых колес ясно, что размеры зуба полностью зависят от профиля инструмента. По ГОСТ профиль инструмента стандартизован путем задания так называемого «исходного контура». На рис.5.9 представлен теоретический исходный контур. Он выполнен в виде рейки с трапециевидными зубьями.
Шаг рейки p - расстояние между одноименными точками двух соседних зубьев. Шаг складывается из толщины зуба s и ширины впадины e. Та единственная прямая, на которой толщина зуба равна ширине впадины, называется делительной прямой рейки., остальные прямые называются начальными. Шаг зубьев рейки p = π m s = e = π m / 2. Делительная прямая делит зуб на головку и ножку. Высота головки – ha = 1.25 m, высота ножки – hf = m, высота всего зуба – h = 2.25 m. Головка закруглена радиусом ρ = 0.38 m. Инструмент изготавливается по производящему исходному контуру, отличающемуся от теоретического исходного контура тем, что впадина сделана глубже на 0.25 m и закруглена так же как головка. Это сделано для того, чтобы впадина инструмента не касалась заготовки. Следовательно, впадина не участвует в нарезании зуба. Зуб нарезают прямолинейные боковые кромки и скругленная вершина зуба. Рейку можно рассматривать как зубчатое колесо бесконечно большого радиуса. В этом случае эвольвента превращается в прямую линию. КОЭФФИЦИЕНТ ПЕРЕКРЫТИЯ Одной из важнейших качественных характеристик зацепления является коэффициент перекрытия. Он характеризует плавность зацепления колес. Коэффициент перекрытия равен отношению угла перекрытия φα к угловому шагу τ: εα= φα / τ (5.3) Угол перекрытия есть угол поворота зубчатого колеса от положения входа зуба в зацепление до положения выхода из зацепления. Его можно определить, рассмотрев два положения зуба – в момент входа и в момент выхода из зацепления (рис. 5.16).
Установим зависимость εα от параметров зацепляющихся колес. Умножим числитель и знаменатель формулы (5.3) на rb - радиус основной окружности. С учетом 4 – го свойства эвольвенты φα rb1 = ab, кроме того, τ1 rb1 = pb - шаг зубьев по основной окружности, следовательно, получим формулу: εα = ав / pb (5.4) Формулу (5.4) можно использовать, если построена картина зацепления, на которой можно замерить длину активной линии зацепления ав. Для получения аналитической зависимости следует представить длину активной линии зацепления в функции от параметров колес. Из построения на рис.5.15 следует: Ав = Рв = аР, Рв = Ав – рА, АР = Ва – РВ. Из треугольников О1Ав и О1АР следует: ав = rb1 tg αa1 РА = rb1 tg αW Из треугольников О2Ва и О2ВР следует Ba = rb2 tg αa2 PB = rb2 tg αW Произведя подстановку полученных выражений в формулу (5.4) и выполнив необходимые преобразования, получим: εα = (z1 (tg αa1 - tg αW) + z2 (tg αa2 – tg αW)) / 2π Здесь аa1 = arccos (db1 / da1) αa2 = arccos (db2/ da2) Как вычисляется αW будет показано в дальнейшем. Коэффициент перекрытия для прямозубых колес должен находиться в пределах 1.2 < εα < 1.98. БЛОКИРУЮЩИЕ КОНТУРЫ Как уже было показано, коэффициенты смещения существенно влияют на качественные показатели зубчатой передачи и ее геометрию. Использование колес со смещением позволяет вписаться в заданное межосевое расстояние. При увеличении x растет контактная и изгибная прочность. Смещение влияет на скорость скольжения профилей, а значит на их износ. Помимо благоприятного влияния увеличение смещения ведет к заострению, интерференции, к снижению коэффициента перекрытия. Невозможно назначить смещение, оптимальное со всех точек зрения. Для каждой отдельной передачи следует рассмотреть всю совокупность эффектов, вызываемых смещением, что представляет весьма трудоемкую задачу. С целью облегчения практического использования колес со смещением разработан метод блокирующих контуров. Результаты расчетов представлены в виде диаграмм, так называемых блокирующих контуров. Они позволяют обоснованно назначать коэффициенты смещения, не прибегая к трудоемким расчетам. Блокирующий контур строится для каждой пары чисел зубьев z1 и z2. На координатных осях откладываются значения x1 и x2 так, что точка А КОСОЗУБЫЕ КОЛЕСА Винтовые колеса с постоянным шагом винтовой линии называются косозубыми. Боковая поверхность зуба образуется чертящей прямой АВ, лежащей в производящей плоскости Р при обкатывании ее вокруг основного цилиндра Q. Если чертящая прямая параллельна образующей основного цилиндра, получается прямозубое колесо, если она составляет с образующей угол βb – косозубое. Каждая точка прямой описывает эвольвенту. Косозубое колесо можно рассматривать как множество прямозубых колес бесконечно малой толщины, сдвинутых друг относительно друга. Боковая поверхность зуба пересекает основной цилиндр по винтовой линии с углом подъема 90˚ - βb Угол подъема винтовой линии, измеренный на поверхности делительного цилиндра, находится на основании зависимости tg β = (r/rb) tg βb.
Pt = pn cos β, следовательно mt = mn cos β. Косозубые колеса изготавливаются тем же инструментом, что и прямозубые. Заготовка разворачивается относительно инструмента на угол β. В нормальном сечении зуб получается таким же, как у соответствующего прямозубого колеса. Размеры зубьев в торцевом сечении рассчитываются по приведенным выше формулам, но модуль принимается торцевой, выраженный через стандартный модуль инструмента.
εγ = εα+ εβ где εα – коэффициент перекрытия соответствующего прямозубого колеса, εβ - добавочный коэффициент перекрытия из-за наклона линии зуба: εβ = φβ / τ, где τ - угловой шаг. Из построения на рис. 5.19 следует: φβ = b tg β / r Достоинство косозубых колес – плавность работы, бесшумность, недостаток наличие осевого усилия на подшипники. Для устранения этого усилия применяют шевронные колеса. ДРУГИЕ ВИДЫ ЗАЦЕПЛЕНИЯ
Разновидностью циклоидального является часовое зацепление, в этом зацеплении эпициклоида головки зуба заменена дугой окружности, а гипоциклоида – прямой (циклоида превращается в прямую, если rn = 0.5 rb (рис. 5.20)). Достоинства зацепления, большие передаточные отношения и уменьшенный износ по сравнению с эвольвентным зацеплением. Другой разновидностью циклоидального зацепления является цевочное зацепление. Боковой профиль зуба шестерни выполняется по эпициклоиде, зуб другого колеса - в виде цилиндрического ролика, называемого цевкой (рис. 5.20 б). При соответствующем выборе параметров профили будут сопряженными. Такое зацепление применяется там, где большое колесо по технологическим соображениям выполнить невозможно, его собирают из дисков, снабженных цевками. Такие колеса применяются, например, для привода поворотных платформ больших экскаваторов. Сравнительно недавно было предложено круговинтовое зацепление (зацепление Новикова). Если в обычном эвольвентном зацеплении зубья касаются по контактной линии, которая перемещается по высоте зуба, то в круговинтовом зацеплении контакт происходит в точке, которая перемещается вдоль зуба. В качестве профилей зубьев здесь используются дуги окружностей (рис. 5.20 в). Так как разница радиусов кривизны невелика, контактные напряжения малы. Поскольку точка контакта перемещается вдоль зуба, высоту зуба можно делать небольшой, тем самым, увеличивая прочность зубьев. Зубчатые колеса с круговинтовыми зубьями, несмотря на их достоинства, нашли ограниченное применение в связи со сложностью изготовления инструмента для их нарезки. ПЛАНЕТАРНЫЕ ЗУБЧАТЫЕ МЕХАНИЗМЫ Планетарным называется зубчатый механизм, содержащий колеса с подвижными осями. Планетарные зубчатые механизмы широко распространены в технике, особенно транспортной, так как, обладая большим передаточным отношением, имеют малые габариты и вес. Иногда эти механизмы называют эпициклическими, так как траектории точек колес с подвижными осями при внешнем зацеплении представляют эпициклоиды. Простейший планетарный механизм представлен на рис. 5.25. Колесо 2 с подвижной осью называется сателлитом, центральное колесо 1 – солнечным, звено, несущее ось сателлита, называется водилом, его принято обозначать буквой Н.
Если колесо 1 подвижно, степень подвижности механизма, рассчитанная по формуле Чебышева, равна 2, Если остановить колесо 1, получим механизм с W = 1 (рис. 5.25б) Механизмы, у которых W>1, называются дифференциальными (зубчатыми дифференциальными). Если у планетарного механизма остановить водило, оставив колеса свободными, получим рядовую передачу. Схема планетарных механизмов могут быть очень разнообразными. Практическое применение нашло, в основном, только несколько схем. Наиболее распространенные схемы представлены на рис. 5.26. Механизм по схеме а получил название механизма Джеймса, а механизм по схеме в – механизм Давида. Наибольшее распространение получила схема а. Она характеризуется высоким к.п.д., практический диапазон передаточных отношений U = 3 – 8. Механизмы по схемам в и г могут иметь очень большие передаточные отношения, но у них низкий к.п.д. По схеме е выполняются мотор – редукторы, представляющие в одном агрегате двигатель и редуктор. Особенно перспективна схема д, здесь всего два колеса, высокий к.п.д., большое передаточное отношение. АНАЛИТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНОГО ОТНОШЕНИЯ И УГЛОВЫХ СКОРОСТЕЙ ПЛАНЕТАРНЫХ МЕХАНИЗМОВ Кинематический расчет планетарных механизмов значительно более сложен, чем рядовых механизмов. Он основан на методе обращения движения. Рассмотрим его на примере механизма на рис. 5.27. Считаем, что заданы числа зубьев колес Z1, Z2, Z3, Z4, угловая скорость входного колеса ω1. Требуется определить передаточное отношение U1н, угловую скорость выходного звена Н и угловую скорость колеса 2.
U14H = (ω1 - ωH) / (ω4 – ωH) (5.12) Здесь верхний индекс Н указывает, что параметры относятся к обращенному механизму. Согласно формуле (5.11) имеем: U14H = - Z2 Z4 / Z1 Z3 Из формулы (5.12) после некоторых преобразований следует: U1H = ω1 / ωH = 1 - U14H Полученная формула справедлива для любой схемы планетарного механизма. Она носит название формулы Виллиса. Если требуется определить передаточное отношение от водила к колесу 1, то, имея в виду, что UH1 = 1 / U1H, получим
Зная U1H, можно найти ωН: ωН = ω1 / U1H. Для определения скорости ω2 следует рассмотреть одну ступень планетарного механизма и изобразить соответствующий ей обращенный механизм (рис.5.28). Для обращенного механизма U12 = (ω1 – ωH) / (ω2 - ωH) Отсюда уже не представляет сложности определить ω2. 5.25 КИНЕМАТИЧЕСКИЙ АНАЛИЗ АВТОМОБИЛЬНОГО ДИФФЕРЕНЦИАЛА
Рассмотренный метод кинематического исследования применим также к анализу дифференциальных зубчатых механизмов. Одним из наиболее известных является автомобильный дифференциал (рис.5.29). Его назначение – передача движения от карданного вала к колесам автомобиля. Механизм, представленный на рис.5.29, включает главную передачу, образованную коническими колесами Z1 и Z2, корпус дифференциала, являющийся в то же время водилом дифференциального механизма, нескольких сателлитов Z4 и двух центральных колес Z3 и Z5, жестко посаженных на полуоси колес. Применим к этому механизму принцип обращения движения, сообщив ему скорость – ωН. На рис. представлен обращенный механизм. Для него можно записать U35H = (ω3 – ωH) / (ω5 – ωH) = Z5 / Z3 Поскольку Z5 = Z3, U35H = -1. Знак минус указывает, что колеса Z3 и Z5 в обращенном механизме вращаются в противоположном направлении. Произведя подстановку, получим уравнение автомобильного дифференциала: Ω3 + ω5 = 2 ωН (5.13) Произведем анализ формулы (5.13). При движении по прямому участку дороги ω3 = ω5 = ωН, следовательно, дифференциал как бы жестко связывает полуоси, происходит кинематическая блокировка дифференциала. Совершенно по другому ведет себя дифференциал при движении по закруглению. Внешнее колесо движется с большой угловой скоростью, чем внутренне, но так, что их средняя скорость равна скорости водила. Если бы колеса были связаны жесткой осью, происходило бы пробуксовка одного или обоих колес, ухудшая эксплуатацию автомобиля. В том случае, когда одно колесо свободно пробуксовывает, второе колесе неподвижно. Скорость буксующего колеса равно 2ωН. В таких случаях применят механическую блокировку дифференциала. ГРАФИЧЕСКИЙ МЕТОД АНАЛИЗА ПЛАНЕТАРНЫХ МЕХАНИЗМОВ В ряде случаев полезно произвести кинематическое исследование планетарного механизма графическим методом. В основе этого метода лежат два положения кинематики: 1. Скорость точки звена, совершающего вращательное движение, является линейной функцией радиуса вращения. В таком случае график зависимости скорости от радиуса есть прямая линия. 2. Любое плоское движение можно рассматривать как мгновенное вращательное движение вокруг МЦС (мгновенного центра скоростей).
В качестве примера рассмотрим механизм, представленный на рис. 5.32. Он включает планетарную и рядовую ступень, составленную колесами Z5 и Z6. Схема механизма должна быть построена в масштабе kl = lOA / OA. Справа от схемы построена линия полюсов р – р. От этой линии откладываются скорости точек звеньев в масштабе kV = VA / pa. Условимся положительные скорости направлять вправо, отрицательные – влево. Точки на линии полюсов находятся в проекционной связи с точками на механизме. Построение плана скоростей начинается с точки А. Скорость точки С равна нулю, эта точка является МЦС для блока сателлитов. Линия са на плане скоростей называется картиной распределения скоростей. Она обладает тем свойством, что на ней находятся концы векторов скоростей точек, лежащих на блоке сателлитов. Это свойство обосновано выше. Тогда, проведя линию проекционной связи, найдем скорость точки В. Соединив точки В и О, получим картину скоростей водила. Дальнейшее построение ясно из рисунка. Покажем, что угловая скорость звена пропорциональна тангенсу угла наклона соответствующей картины скоростей. Это следует из соотношения: Ω1 = VA / LOA = tg α kω (5.14) Аналогичные выражения можно записать для угловых скоростей остальных звеньев. Формула (5.14) позволяет по углу наклона найти угловые скорости. Однако можно избегнуть необходимости этого расчета, если произвести дополнительное построение плана угловых скоростей. Выбирается произвольный вертикальный отрезок sk, из точки к строятся под углами α лучи до пересечения с горизонталью, проведенной через точку s. Из построений следует, что, например, tg α = sa / sk. Следовательно отрезки sa, sc, sb, se выражают в масштабе угловые скорости ω1, ω2, ωН, ω6. Графическое исследование дифференциального механизма производится аналогично, с той лишь разницей, что скорость точки С принимается равной нулю. УСЛОВИЯ СООСНОСТИ, СОСЕДСТВА, СБОРКИ ПЛАНЕТАРНЫХ МЕХАНИЗМОВ
а + b = c + d Поскольку колеса изображены их делительными окружностями, то нетрудно через диаметры делительных окружностей записанное выше равенство представить в виде: Z1 + Z2 = Z3 + Z4 Аналогичным образом для механизма по схеме б получено условие: Z1 + Z2 = Z4 – Z3
2 r2a < 2 RH sin π / k где r2a - радиус окружности вершин сателлита, RH – радиус водила, k – число сателлитов в механизме. Выразив радиусы через модули и числа зубьев, и произведя преобразования, получим: Sin π / k > (Z2 + 2) / (Z1 + Z2) (5.15) Формула (5.15) позволяет подсчитать максимальное число сателлитов. Впрочем, эту задачу можно решить и чисто графически.
Будем считать, что сателлит имеет четное число зубьев, тогда впадины на центральных колесах можно расположить друг против друга. Повернем колесо 1 на целое число Е угловых шагов φ1Е = Е φ1, где φ1 = 2π/Z1. Тогда впадины между зубьями расположатся друг против друга и можно поставить следующий сателлит. Подсчитаем угол поворота водила: Φ1Е / φHE = U1H, Отсюда ΦH E = 2π E / Z1 U1H Воспользовавшись формулой Виллиса, выразим U1H через U13H и преобразуем вышезаписанную формулу: ΦHE = 2π E / (Z1 + Z3) Таким путем можно установить к сателлитов, если расположить их равномерно: к = 2π/ φHE = (Z1 + Z3) / E Поскольку к – целое число, Z1 + Z3 должно быть кратно числу сателлитов. Аналогичные результаты получены и при нечетном числе зубьев сателлитов. Для передач с двойными сателлитами условие сборки можно получить аналогичным образом. ПРИМЕР СИНТЕЗА ПЛАНЕТАРНОГО МЕХАНИЗМА
1. Определяем передаточное отношение соответствующего обращенного механизма: U14H 1 – U1H = - 11 2.Разложим полученное передаточное отношение на множители. Здесь возможны разнообразные варианты, например: U14H = Z2 Z4 / Z1 Z3 = 220 / 20 =4 ▪ 55 / 4 ▪ 5 3.Запишем условие соосности и проверим его выполнение для принятых чисел зубьев: Z1 + Z2 = 4 + 4 = 8 Z4 – Z3 = 55 – 5 = 50 4.Условие соосности, как правило, не выполняется. Для его выполнения нужно умножить верхнюю формулу на 50, а нижнюю – на 8. Тогда Z1 = 200 Z2 = 200 Z4 = 440 Z3 = 40 Полученные числа зубьев можно сократить так, чтобы получились реально выполнимые колеса с числом зубьев в пределах 10 – 100. ВОЛНОВАЯ ПЕРЕДАЧА
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 3466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.209 (0.014 с.) |

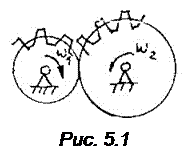 Зубчатые механизмы предназначены для передачи вращательного движения и преобразования его параметров. Обычно двигатели обладают скоростью и моментом, как правило, не подходящим для использования в технологическом процессе. Преобразование параметров вращательного движения возможно посредством прижатых друг к другу гладких дисков (рис. 5.1), образующих фрикционные передачи. Ее недостаток – ограниченная мощность из-за большой нагрузки на подшипники, неизбежное проскальзывание, износ поверхностей, потери мощности. Практически передаваемая мощность в таких механизмах не превышает 10 – 20 квт.
Зубчатые механизмы предназначены для передачи вращательного движения и преобразования его параметров. Обычно двигатели обладают скоростью и моментом, как правило, не подходящим для использования в технологическом процессе. Преобразование параметров вращательного движения возможно посредством прижатых друг к другу гладких дисков (рис. 5.1), образующих фрикционные передачи. Ее недостаток – ограниченная мощность из-за большой нагрузки на подшипники, неизбежное проскальзывание, износ поверхностей, потери мощности. Практически передаваемая мощность в таких механизмах не превышает 10 – 20 квт.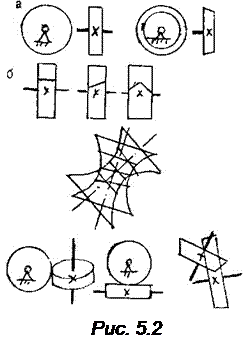 В гиперболоидных передачах звенья выполняются в форме гиперболоида вращения. Гиперболоид – линейчатая поверхность, образуемая при вращении произвольно расположенной в пространстве прямой линии относительно некоторой оси. Таким образом, образующей поверхности гиперболоида является прямая линия. Два сопряженных гиперболоида перекатываются друг по другу без скольжения и касаются по прямой линии. Если их снабдить зубьями, образуется точная гиперболоидная передача (рис. 5.2). На практике используется приближенная гиперболоидная передача, образованная из цилиндрических и конических колес. В таком случае касание их происходит не по линии, а в точке. Различают винтовые, червячные и гипоидные передачи (рис. 5.2). Различают также понижающие и повышающие частоту вращения передачи (редукторы и мультипликаторы), передачи внешнего, внутреннего зацепления, реечные передачи. Зубчатые механизмы бывают: а) с неподвижными осями колес (рядовые) и с подвижными осями (планетарные), б) предназначенные для передачи большой мощности (силовые) и для преобразования параметров движения (кинематические), в) с одной степенью подвижности и зубчатые дифференциалы.
В гиперболоидных передачах звенья выполняются в форме гиперболоида вращения. Гиперболоид – линейчатая поверхность, образуемая при вращении произвольно расположенной в пространстве прямой линии относительно некоторой оси. Таким образом, образующей поверхности гиперболоида является прямая линия. Два сопряженных гиперболоида перекатываются друг по другу без скольжения и касаются по прямой линии. Если их снабдить зубьями, образуется точная гиперболоидная передача (рис. 5.2). На практике используется приближенная гиперболоидная передача, образованная из цилиндрических и конических колес. В таком случае касание их происходит не по линии, а в точке. Различают винтовые, червячные и гипоидные передачи (рис. 5.2). Различают также понижающие и повышающие частоту вращения передачи (редукторы и мультипликаторы), передачи внешнего, внутреннего зацепления, реечные передачи. Зубчатые механизмы бывают: а) с неподвижными осями колес (рядовые) и с подвижными осями (планетарные), б) предназначенные для передачи большой мощности (силовые) и для преобразования параметров движения (кинематические), в) с одной степенью подвижности и зубчатые дифференциалы.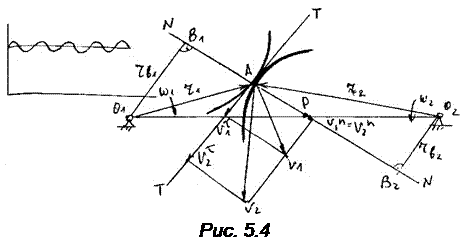
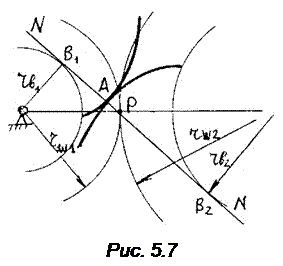 На рис. 5.7 представлено зацепление эвольвентных профилей. Общая нормаль N – N. Проведенная через точку касания двух профилей, обязана согласно 1-му свойству эвольвенты, коснуться основных окружностей. Поскольку таких окружностей две, положение нормали единственно и неизменно. Тем самым подтверждается выполнение следствия основного закона зацепления. В процессе зацепления точка касания профилей не может сойти с общей нормали N – N, т.к. в противном случае нарушилось бы 1-ое свойство. Установлено, что при эвольвентном зацеплении профилей точка касания движется по общей нормали с постоянной скоростью.
На рис. 5.7 представлено зацепление эвольвентных профилей. Общая нормаль N – N. Проведенная через точку касания двух профилей, обязана согласно 1-му свойству эвольвенты, коснуться основных окружностей. Поскольку таких окружностей две, положение нормали единственно и неизменно. Тем самым подтверждается выполнение следствия основного закона зацепления. В процессе зацепления точка касания профилей не может сойти с общей нормали N – N, т.к. в противном случае нарушилось бы 1-ое свойство. Установлено, что при эвольвентном зацеплении профилей точка касания движется по общей нормали с постоянной скоростью. При способе обкатки инструмент и заготовка совершают относительное движение обкатывания, инструмент своими режущими кромками постепенно внедряется в заготовку, прокладывая себе путь. Таким образом, возникает станочное зацепление, аналогичное обычному зацеплению с той разницей, что одно из звеньев является инструментом. Инструмент выполняется в виде гребенки, червячной фрезы или долбяка. Этот способ требует применения специальных зубофрезерных станков. В одних конструкциях станков инструмент обкатывается вокруг неподвижной заготовки, в других – инструмент движется поступательно, заготовка поворачивается, в третьих – заготовка и инструмент (долбяк) вращаются (рис.5.8).
При способе обкатки инструмент и заготовка совершают относительное движение обкатывания, инструмент своими режущими кромками постепенно внедряется в заготовку, прокладывая себе путь. Таким образом, возникает станочное зацепление, аналогичное обычному зацеплению с той разницей, что одно из звеньев является инструментом. Инструмент выполняется в виде гребенки, червячной фрезы или долбяка. Этот способ требует применения специальных зубофрезерных станков. В одних конструкциях станков инструмент обкатывается вокруг неподвижной заготовки, в других – инструмент движется поступательно, заготовка поворачивается, в третьих – заготовка и инструмент (долбяк) вращаются (рис.5.8). Размеры рейки выражаются через один основной параметр, называемый модулем. Модуль m имеет размерность мм и выбирается из ряда рациональных чисел от 0.05 до 100.
Размеры рейки выражаются через один основной параметр, называемый модулем. Модуль m имеет размерность мм и выбирается из ряда рациональных чисел от 0.05 до 100.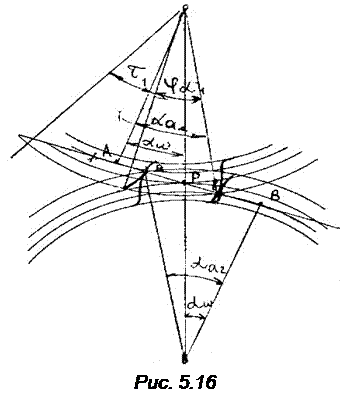 Угол перекрытия должен быть больше углового шага. Благодаря этому первая пара зубьев еще не успевает разомкнуться (придти в точку в) как вторая пара зубьев входит в зацепление. Таким образом, существуют периоды двухпарного зацепления. Это обеспечивает непрерывность зацепления. Чем больше εα, тем плавнее работает передача.
Угол перекрытия должен быть больше углового шага. Благодаря этому первая пара зубьев еще не успевает разомкнуться (придти в точку в) как вторая пара зубьев входит в зацепление. Таким образом, существуют периоды двухпарного зацепления. Это обеспечивает непрерывность зацепления. Чем больше εα, тем плавнее работает передача. соответствует передаче, составленной из колес с положительным смещением, точка В – с отрицательным смещением, точка 0 - для нулевых колес (рис. 5.17). Таким образом, каждой точке координатного поля соответствует вариант передачи. Однако не все точки этого поля можно использовать. Некоторые неприемлемы по условию существования передачи: интерференции, подрезания, заострения, малого коэффициента перекрытия. Предельно допустимому значению каждого этого параметра соответствуют безусловные границы, эти границы в виде линий в совокупности образуют блокирующий контур. Для каждой пары чисел зубьев формы контура будут разными. Внутри контура могут быть нанесены условные границы, например, εα = 1.2, sa = 0.25 m, x = xmin и т. д. Блокирующие контуры для различных сочетаний чисел зубьев колес содержаться в соответствующих справочниках.
соответствует передаче, составленной из колес с положительным смещением, точка В – с отрицательным смещением, точка 0 - для нулевых колес (рис. 5.17). Таким образом, каждой точке координатного поля соответствует вариант передачи. Однако не все точки этого поля можно использовать. Некоторые неприемлемы по условию существования передачи: интерференции, подрезания, заострения, малого коэффициента перекрытия. Предельно допустимому значению каждого этого параметра соответствуют безусловные границы, эти границы в виде линий в совокупности образуют блокирующий контур. Для каждой пары чисел зубьев формы контура будут разными. Внутри контура могут быть нанесены условные границы, например, εα = 1.2, sa = 0.25 m, x = xmin и т. д. Блокирующие контуры для различных сочетаний чисел зубьев колес содержаться в соответствующих справочниках. Рассмотрим развертку делительного цилиндра на плоскости + рис.(5.18).На ней можно указать три шага зубьев: нормальный pn, торцевой pt, осевой pa. Соответственно этому имеется три модуля: нормальный mn, торцевой mt, осевой ma. Из построения на рис. следует, что
Рассмотрим развертку делительного цилиндра на плоскости + рис.(5.18).На ней можно указать три шага зубьев: нормальный pn, торцевой pt, осевой pa. Соответственно этому имеется три модуля: нормальный mn, торцевой mt, осевой ma. Из построения на рис. следует, что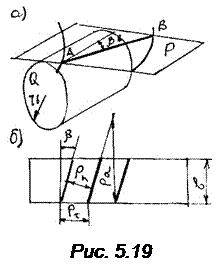 Основная особенность косозубых колес состоит в том, что зубья входят в зацепление не по всей длине зуба, как это происходит в прямозубых колесах, а по контактной линии, параллельной образующей основного цилиндра, длина которой непрерывно изменяется. Благодаря этому увеличивается продолжительность контакта пары зубьев, что находит выражение в увеличении коэффициента перекрытия. Для косозубых колес коэффициент перекрытия
Основная особенность косозубых колес состоит в том, что зубья входят в зацепление не по всей длине зуба, как это происходит в прямозубых колесах, а по контактной линии, параллельной образующей основного цилиндра, длина которой непрерывно изменяется. Благодаря этому увеличивается продолжительность контакта пары зубьев, что находит выражение в увеличении коэффициента перекрытия. Для косозубых колес коэффициент перекрытия Помимо эвольвентного ограниченное распространение получили другие виды зацепления. В прошлом было широко распространено циклоидальное (циклоидное) зацепление. Если чертящую точку взять не на прямой, а на производящей окружности, и перекатывать ее по основной окружности, чертящая точка будет описывать кривую, называемую циклоидой. Причем, если производящая окружность катится снаружи основной, будет эпициклоида, если внутри – гипоциклоида. В циклоидальном зубчатом колесе профиль головки зуба выполняется по эпициклоиде, а профиль ножки зуба – по гипоциклоиде. Преимущество циклоидального зацепления – контакт выпукло- вогнутых поверхностей и, как следствие, уменьшение контактных напряжений. Недостаток – нельзя изменять межцентровое расстояние и вообще менять колеса в парах.
Помимо эвольвентного ограниченное распространение получили другие виды зацепления. В прошлом было широко распространено циклоидальное (циклоидное) зацепление. Если чертящую точку взять не на прямой, а на производящей окружности, и перекатывать ее по основной окружности, чертящая точка будет описывать кривую, называемую циклоидой. Причем, если производящая окружность катится снаружи основной, будет эпициклоида, если внутри – гипоциклоида. В циклоидальном зубчатом колесе профиль головки зуба выполняется по эпициклоиде, а профиль ножки зуба – по гипоциклоиде. Преимущество циклоидального зацепления – контакт выпукло- вогнутых поверхностей и, как следствие, уменьшение контактных напряжений. Недостаток – нельзя изменять межцентровое расстояние и вообще менять колеса в парах.

 Сущность метода обращения движения состоит в следующем: придадим стойке механизма скорость вращения водила ωн , но в противоположном направлении. Тогда водило окажется неподвижным в абсолютной системе отсчета, а остальные звенья приобретут дополнительную скорость – ωн. Изобразим обращенный механизм рядом на схеме. Механизм с неподвижным водилом является зубчатым рядом, для него справедливы полученные ранее соотношения:
Сущность метода обращения движения состоит в следующем: придадим стойке механизма скорость вращения водила ωн , но в противоположном направлении. Тогда водило окажется неподвижным в абсолютной системе отсчета, а остальные звенья приобретут дополнительную скорость – ωн. Изобразим обращенный механизм рядом на схеме. Механизм с неподвижным водилом является зубчатым рядом, для него справедливы полученные ранее соотношения: UH1 = 1 / (1 - U14H)
UH1 = 1 / (1 - U14H)

 В отличие от рядовых механизмов планетарный механизм может существовать только при выполнении определенных соотношений между числами зубьев колес. Прежде всего должно быть выполнено условие соосности. Оно состоит в том, что оси центральных, солнечного и опорного, колес, а также водила должны совпадать. В противном случае механизм заклинит. Из рассмотрения схем на рис.5.33. следует:
В отличие от рядовых механизмов планетарный механизм может существовать только при выполнении определенных соотношений между числами зубьев колес. Прежде всего должно быть выполнено условие соосности. Оно состоит в том, что оси центральных, солнечного и опорного, колес, а также водила должны совпадать. В противном случае механизм заклинит. Из рассмотрения схем на рис.5.33. следует: Условие соседства сателлитов выражается в том, что соседние сателлиты не должны касаться друг друга окружностями вершин (рис.5.34) Из геометрических построений соотношение:
Условие соседства сателлитов выражается в том, что соседние сателлиты не должны касаться друг друга окружностями вершин (рис.5.34) Из геометрических построений соотношение: При сборке трехколесного планетарного механизма может оказаться, что после установки первого сателлита остальные сателлиты установить нельзя. Это происходит потому, что поставленный первым сателлит полностью определяет взаимное положение центральных колес. Установим условия, налагаемые на числа зубьев, при которых будет происходить собираемость механизма (рис. 5.35)
При сборке трехколесного планетарного механизма может оказаться, что после установки первого сателлита остальные сателлиты установить нельзя. Это происходит потому, что поставленный первым сателлит полностью определяет взаимное положение центральных колес. Установим условия, налагаемые на числа зубьев, при которых будет происходить собираемость механизма (рис. 5.35) Рассмотрим методику синтеза планетарного механизма, ограничиваясь соблюдением условия заданного передаточного отношения и условия соосности. Пусть выбрана схема механизма (рис.5.36), для которой надо подобрать числа зубьев, обеспечивающие передаточное отношение, например, равное 12.
Рассмотрим методику синтеза планетарного механизма, ограничиваясь соблюдением условия заданного передаточного отношения и условия соосности. Пусть выбрана схема механизма (рис.5.36), для которой надо подобрать числа зубьев, обеспечивающие передаточное отношение, например, равное 12. В 1959 году Массер (США) запатентовал зубчатую передачу, которая в настоящее время пользуется большой популярностью. Ее основные достоинства – большое передаточное отношение, высокий к.п.д., способность передавать движение в герметичные полости, многопарность зацепления (до 30% зубьев), малое скольжение и износ. В волновой передаче одно из колес выполняется гибким, способным деформироваться под действием звена, называемого генератором волн. Волновые передачи весьма разнообразны. Чаще всего они выполняются с неподвижным жестким звеном и внутренним гибким колесом. Возможны двухволновые и многоволновые механизмы с генератором в виде эллипсов
В 1959 году Массер (США) запатентовал зубчатую передачу, которая в настоящее время пользуется большой популярностью. Ее основные достоинства – большое передаточное отношение, высокий к.п.д., способность передавать движение в герметичные полости, многопарность зацепления (до 30% зубьев), малое скольжение и износ. В волновой передаче одно из колес выполняется гибким, способным деформироваться под действием звена, называемого генератором волн. Волновые передачи весьма разнообразны. Чаще всего они выполняются с неподвижным жестким звеном и внутренним гибким колесом. Возможны двухволновые и многоволновые механизмы с генератором в виде эллипсов 


