
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический расчет зубчатой передачиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При построении картины зацепления межосевое расстояние О1О2 определяется по формуле (5.2). Диаметры начальных окружностей можно найти, рассмотрев треугольники О1АР и О2ВР: dW1 = mz1 (cos20˚ / cos αW) (5.6) dW2 = mz2 (cos 20˚ / cos αW) В таком случае начальное межосевое расстояние рассчитывается по формуле aW = 0.5 m (z1 + z2) (cos20˚ / cos αW) (5.7) Как уже указывалось, при работе зубчатой передачи начальные окружности перекатываются друг по другу без скольжения. В случае беззазорного зацепления толщина зуба на начальной окружности одного колеса равна ширине впадины на начальной окружности другого колеса sW1 = eW2 Выполнив подстановку соответствующих выражений для толщины зуба и ширины впадины и произведя соответствующие преобразования, получим: inv αW = 2 tg20˚ (x1 + x2) / (z1 + z2) + inv20˚ (5.8) Полученное выражение называется уравнением зацепления, оно позволяет определить угол зацепления, исходя из заданных чисел зубьев и коэффициентов смещений. Формулы (5.6). (5.7), (5.8) образуют основу для геометрического расчета зубчатой передачи. В зависимости от сочетания коэффициентов смещений различают четыре варианта передач, представленных в таблице
Иногда формулу (5.6) представляют в виде: аW = a + y m Где y - коэффициент воспринимаемого смещения: y = 0.5 (z1 + x2) (cos 20˚ - cos αW) / cos αW
ошибка! Надо z1+z2!
Кроме того, вводится обозначение ∆ y = ∑ x - y где ∆y - коэффициент уравнительного смещения. Согласно ГОСТ 16132- 72 расчет геометрических параметров зубчатой перeдачи следует вести с использованием этих коэффициентов. БЛОКИРУЮЩИЕ КОНТУРЫ Как уже было показано, коэффициенты смещения существенно влияют на качественные показатели зубчатой передачи и ее геометрию. Использование колес со смещением позволяет вписаться в заданное межосевое расстояние. При увеличении x растет контактная и изгибная прочность. Смещение влияет на скорость скольжения профилей, а значит на их износ. Помимо благоприятного влияния увеличение смещения ведет к заострению, интерференции, к снижению коэффициента перекрытия. Невозможно назначить смещение, оптимальное со всех точек зрения. Для каждой отдельной передачи следует рассмотреть всю совокупность эффектов, вызываемых смещением, что представляет весьма трудоемкую задачу. С целью облегчения практического использования колес со смещением разработан метод блокирующих контуров. Результаты расчетов представлены в виде диаграмм, так называемых блокирующих контуров. Они позволяют обоснованно назначать коэффициенты смещения, не прибегая к трудоемким расчетам. Блокирующий контур строится для каждой пары чисел зубьев z1 и z2. На координатных осях откладываются значения x1 и x2 так, что точка А КОСОЗУБЫЕ КОЛЕСА Винтовые колеса с постоянным шагом винтовой линии называются косозубыми. Боковая поверхность зуба образуется чертящей прямой АВ, лежащей в производящей плоскости Р при обкатывании ее вокруг основного цилиндра Q. Если чертящая прямая параллельна образующей основного цилиндра, получается прямозубое колесо, если она составляет с образующей угол βb – косозубое. Каждая точка прямой описывает эвольвенту. Косозубое колесо можно рассматривать как множество прямозубых колес бесконечно малой толщины, сдвинутых друг относительно друга. Боковая поверхность зуба пересекает основной цилиндр по винтовой линии с углом подъема 90˚ - βb Угол подъема винтовой линии, измеренный на поверхности делительного цилиндра, находится на основании зависимости tg β = (r/rb) tg βb.
Pt = pn cos β, следовательно mt = mn cos β. Косозубые колеса изготавливаются тем же инструментом, что и прямозубые. Заготовка разворачивается относительно инструмента на угол β. В нормальном сечении зуб получается таким же, как у соответствующего прямозубого колеса. Размеры зубьев в торцевом сечении рассчитываются по приведенным выше формулам, но модуль принимается торцевой, выраженный через стандартный модуль инструмента.
εγ = εα+ εβ где εα – коэффициент перекрытия соответствующего прямозубого колеса, εβ - добавочный коэффициент перекрытия из-за наклона линии зуба: εβ = φβ / τ, где τ - угловой шаг. Из построения на рис. 5.19 следует: φβ = b tg β / r Достоинство косозубых колес – плавность работы, бесшумность, недостаток наличие осевого усилия на подшипники. Для устранения этого усилия применяют шевронные колеса. ДРУГИЕ ВИДЫ ЗАЦЕПЛЕНИЯ
Разновидностью циклоидального является часовое зацепление, в этом зацеплении эпициклоида головки зуба заменена дугой окружности, а гипоциклоида – прямой (циклоида превращается в прямую, если rn = 0.5 rb (рис. 5.20)). Достоинства зацепления, большие передаточные отношения и уменьшенный износ по сравнению с эвольвентным зацеплением. Другой разновидностью циклоидального зацепления является цевочное зацепление. Боковой профиль зуба шестерни выполняется по эпициклоиде, зуб другого колеса - в виде цилиндрического ролика, называемого цевкой (рис. 5.20 б). При соответствующем выборе параметров профили будут сопряженными. Такое зацепление применяется там, где большое колесо по технологическим соображениям выполнить невозможно, его собирают из дисков, снабженных цевками. Такие колеса применяются, например, для привода поворотных платформ больших экскаваторов. Сравнительно недавно было предложено круговинтовое зацепление (зацепление Новикова). Если в обычном эвольвентном зацеплении зубья касаются по контактной линии, которая перемещается по высоте зуба, то в круговинтовом зацеплении контакт происходит в точке, которая перемещается вдоль зуба. В качестве профилей зубьев здесь используются дуги окружностей (рис. 5.20 в). Так как разница радиусов кривизны невелика, контактные напряжения малы. Поскольку точка контакта перемещается вдоль зуба, высоту зуба можно делать небольшой, тем самым, увеличивая прочность зубьев. Зубчатые колеса с круговинтовыми зубьями, несмотря на их достоинства, нашли ограниченное применение в связи со сложностью изготовления инструмента для их нарезки.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 653; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.77 (0.009 с.) |

 соответствует передаче, составленной из колес с положительным смещением, точка В – с отрицательным смещением, точка 0 - для нулевых колес (рис. 5.17). Таким образом, каждой точке координатного поля соответствует вариант передачи. Однако не все точки этого поля можно использовать. Некоторые неприемлемы по условию существования передачи: интерференции, подрезания, заострения, малого коэффициента перекрытия. Предельно допустимому значению каждого этого параметра соответствуют безусловные границы, эти границы в виде линий в совокупности образуют блокирующий контур. Для каждой пары чисел зубьев формы контура будут разными. Внутри контура могут быть нанесены условные границы, например, εα = 1.2, sa = 0.25 m, x = xmin и т. д. Блокирующие контуры для различных сочетаний чисел зубьев колес содержаться в соответствующих справочниках.
соответствует передаче, составленной из колес с положительным смещением, точка В – с отрицательным смещением, точка 0 - для нулевых колес (рис. 5.17). Таким образом, каждой точке координатного поля соответствует вариант передачи. Однако не все точки этого поля можно использовать. Некоторые неприемлемы по условию существования передачи: интерференции, подрезания, заострения, малого коэффициента перекрытия. Предельно допустимому значению каждого этого параметра соответствуют безусловные границы, эти границы в виде линий в совокупности образуют блокирующий контур. Для каждой пары чисел зубьев формы контура будут разными. Внутри контура могут быть нанесены условные границы, например, εα = 1.2, sa = 0.25 m, x = xmin и т. д. Блокирующие контуры для различных сочетаний чисел зубьев колес содержаться в соответствующих справочниках. Рассмотрим развертку делительного цилиндра на плоскости + рис.(5.18).На ней можно указать три шага зубьев: нормальный pn, торцевой pt, осевой pa. Соответственно этому имеется три модуля: нормальный mn, торцевой mt, осевой ma. Из построения на рис. следует, что
Рассмотрим развертку делительного цилиндра на плоскости + рис.(5.18).На ней можно указать три шага зубьев: нормальный pn, торцевой pt, осевой pa. Соответственно этому имеется три модуля: нормальный mn, торцевой mt, осевой ma. Из построения на рис. следует, что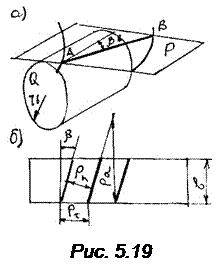 Основная особенность косозубых колес состоит в том, что зубья входят в зацепление не по всей длине зуба, как это происходит в прямозубых колесах, а по контактной линии, параллельной образующей основного цилиндра, длина которой непрерывно изменяется. Благодаря этому увеличивается продолжительность контакта пары зубьев, что находит выражение в увеличении коэффициента перекрытия. Для косозубых колес коэффициент перекрытия
Основная особенность косозубых колес состоит в том, что зубья входят в зацепление не по всей длине зуба, как это происходит в прямозубых колесах, а по контактной линии, параллельной образующей основного цилиндра, длина которой непрерывно изменяется. Благодаря этому увеличивается продолжительность контакта пары зубьев, что находит выражение в увеличении коэффициента перекрытия. Для косозубых колес коэффициент перекрытия Помимо эвольвентного ограниченное распространение получили другие виды зацепления. В прошлом было широко распространено циклоидальное (циклоидное) зацепление. Если чертящую точку взять не на прямой, а на производящей окружности, и перекатывать ее по основной окружности, чертящая точка будет описывать кривую, называемую циклоидой. Причем, если производящая окружность катится снаружи основной, будет эпициклоида, если внутри – гипоциклоида. В циклоидальном зубчатом колесе профиль головки зуба выполняется по эпициклоиде, а профиль ножки зуба – по гипоциклоиде. Преимущество циклоидального зацепления – контакт выпукло- вогнутых поверхностей и, как следствие, уменьшение контактных напряжений. Недостаток – нельзя изменять межцентровое расстояние и вообще менять колеса в парах.
Помимо эвольвентного ограниченное распространение получили другие виды зацепления. В прошлом было широко распространено циклоидальное (циклоидное) зацепление. Если чертящую точку взять не на прямой, а на производящей окружности, и перекатывать ее по основной окружности, чертящая точка будет описывать кривую, называемую циклоидой. Причем, если производящая окружность катится снаружи основной, будет эпициклоида, если внутри – гипоциклоида. В циклоидальном зубчатом колесе профиль головки зуба выполняется по эпициклоиде, а профиль ножки зуба – по гипоциклоиде. Преимущество циклоидального зацепления – контакт выпукло- вогнутых поверхностей и, как следствие, уменьшение контактных напряжений. Недостаток – нельзя изменять межцентровое расстояние и вообще менять колеса в парах.


