
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверочный расчёт закрытой цилиндрической передачиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Проверка контактной выносливости рабочих поверхностей зубьев колёс. Расчётом должна быть проверена справедливость соблюдения следующих неравенств [1]: - для прямозубых колёс
- для косозубых колёс
где ZH - коэффициент повышения прочности косозубых передач по контактным напряжениям, Все геометрические параметры рассчитываемых колёс определены в п.2.4. Для косозубой передачи дополнительно рассчитывают
Здесь также знак "+" относится к передачам внешнего зацепления, а "-" -внутреннего зацепления. Рассчитывают (или уточняют) величину вращающего момента Т1 в Нмм на шестерне проверяемой передачи:
где - КПД передачи, он учитывает потери мощности в зубчатой передаче; обычно = 0,97. Для определения коэффициента внутренней динамической нагрузки
Таблица 2.6
Степени точности зубчатых передач
Затем по табл. 2.7 находят значение коэффициента В косозубой передаче теоретически зацепляется одновременно не менее двух пар зубьев. Однако практически ошибки нарезания зубьев могут устранить двухпарное зацепление, и при контакте одной пары между зубьями второй пары может быть небольшой зазор, который устраняется под нагрузкой вследствие упругих деформаций зубьев. Это учитывают коэффициентом KH, назначаемым из табл. 2.8.
Таблица 2.7
Значения коэффициентов KHv и KFv
Примечания: 1. Твёрдость поверхностей зубьев
2. Верхние цифры относятся к прямым зубьям, нижние – к косым зубьям. Таблица 2.8
Если в результате проверки выявится существенная недогрузка (свыше 10 %) передачи, то с целью более полного использования возможностей материалов зубчатых колёс возможна корректировка рабочей ширины зубчатого венца по соотношению Уточнённое значение рабочей ширины венца рекомендуется округлить до нормального линейного размера (по табл.2.5).
Проверка прочности зубьев по напряжениям изгиба. Расчёт выполняют отдельно для шестерни и для зубчатого колеса передачи после уточнения нагрузок на зубчатые колёса и их геометрических параметров. Проверяют справедливость соотношения расчётных напряжений изгиба F и допускаемых напряжений [F]: для прямозубых колёс
и для косозубых колёс
где Окружное усилие в зацеплении колёс рассчитывают по формуле
Коэффициент неравномерности распределения нагрузки по длине линии контакта KF определяют по графикам рис. 2.7 в, аналогично рассмотренному выше определению значения коэффициента KH. Коэффициент формы зуба YF для прямозубых колёс назначают по табл. 2.9 в зависимости от фактического числа зубьев для прямозубых колёс и от числа зубьев эквивалентных колёс Если при проверочном расчёте рабочие напряжения изгиба Таблица 2.9 Коэффициент формы зуба YF
2.5. Расчёт открытой цилиндрической зубчатой передачи Учитывая условия и характер работы открытых передач (недостаточная защищённость от загрязнения абразивными частицами и увеличенный абразивный износ при плохой смазке, большие деформации валов, что приводит к увеличению зазоров в зацеплении, возрастанию динамических нагрузок, к понижению прочности изношенных зубьев вследствие уменьшения площади их поперечного сечения и, как следствие, к поломке зубьев), данные передачи рекомендуют рассчитывать по напряжениям изгиба. В этих передачах выкрашивание не наблюдается, так как поверхностные слои зубьев изнашиваются и удаляются раньше, чем появляются усталостные трещины. Для проектного расчёта открытых передач по напряжениям изгиба определяют модуль зацепления из выражений [1]: для прямозубых колес
для косозубых колес
Здесь:
[F1] - допускаемое напряжение изгиба зубьев шестерни, Н/мм2, определяют в соответствии с п.2.2. («Расчет допускаемых напряжений»); Т3 - момент на шестерне, Нмм;
КF - смотри рис. 2.3, б; YF3 - смотри табл. 2.9. Полученное значение модуля округляют в большую сторону до значения из стандартного ряда модулей (см. п.2.4). Зная значение модуля, определяют геометрические размеры шестерни: диаметр делительный - диаметр вершин зубьев - диаметр впадин зубьев - ширина венца - Точность вычисления диаметров шестерни до 0,001 мм, значение ширины зубчатого венца округляют до целого числа по нормальным линейным размерам (см. табл. 2.5). Проверочный расчет такой передачи по контактным напряжениям выполняют в соответствии с п.2.5. («Проверочный расчет закрытой цилиндрической передачи»).
ПЛАНЕТАРНЫЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ Планетарными называют передачи, имеющие зубчатые колёса с перемещающимися осями [8,29]. Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение, называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси.
Планетарные передачи имеют ряд преимуществ перед обычными: + большие передаточные отношения при малых габаритах и массе; + возможность сложения или разложения механической мощности; + лёгкое управление и регулирование скорости; + малый шум вследствие замыкания сил в механизме. В планетарных передачах широко применяют внутреннее зубчатое зацепление с углом aw = 30о. Для обеспечения сборки планетарных передач необходимо соблюдать условие соосности (совпадение геометрических центров колёс); условие сборки (сумма зубьев центральных колёс кратна числу сателлитов) и соседства (вершины зубьев сателлитов не соприкасаются друг с другом). Зубчатые колёса планетарных передач рассчитываются по тем же законам, что и колёса обычных цилиндрических передач [39]. ВОЛНОВЫЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
Идея волновых передач заключается в наличии нескольких пар зацепления, которые ещё и перемещаются по окружности, за счёт чего достигается огромное передаточное отношение (обычно U60 ¸ 300, известны конструкции с U > 1000). И это в одной ступени!
Такая передача была запатентована американским инженером Массером в 1959 г. Волновые передачи имеют меньшие массу и габариты, большую кинематическую точность, меньший мёртвый ход, высокую вибропрочность за счёт демпфирования (рассеяния энергии) колебаний, создают меньший шум. При необходимости такие передачи позволяют передавать движение в герметичное пространство без применения уплотняющих сальников, что особенно ценно для авиационной, космической и подводной техники, а также для машин химической промышленности.
К недостаткам волновых передач относятся: ` ограниченные обороты ведущего вала (во избежание больших центробежных сил инерции некруглого генератора волн); ` мелкие модули зубьев (1,5 – 2 мм); ` практически индивидуальное, дорогостоящее, весьма трудоёмкое изготовление гибкого колеса и генератора.
Основные виды поломок волновых передач: · разрушение подшипника генератора волн от нагрузки в зацеплении; · проскакивание генератора волн при больших вращающих моментах, когда зубья на входе в зацепление упираются друг в друга вершинами; · поломка гибкого колеса от трещин усталости (особенно при U < 80); · износ зубьев на концах; · пластические деформации боковых поверхностей зубьев при перегрузках. Расчёт волновых зубчатых передач отличается от расчёта обычных зубчатых передач тем, что учитывается деформация гибкого венца и генератора [40]. За критерий работоспособности обычно принимают допускаемые напряжения смятия где Yd – коэффициент ширины гибкого венца; d – делительный диаметр гибкого венца.
ЗАЦЕПЛЕНИЯ НОВИКОВА
Итак, основной недостаток зубчатых передач с эвольвентным профилем (цилиндрических, конических, планетарных, волновых) – высокие контактные напряжения в зубьях. Они велики потому, что контактируют два зуба с выпуклыми профилями. При этом площадка контакта очень мала, а контактные напряжения соответственно высоки. Это обстоятельство сильно ограничивает "несущую способность" передач, т.е. не позволяет передавать большие вращающие моменты.
К тому же выпуклый и вогнутый профили (обычно круговые) имеют близкие по абсолютной величине радиусы кривизны. За счёт этого получается большая площадка контакта, контактные напряжения уменьшаются и появляется возможность передавать примерно в 1,4 ¸ 1,8 раза большие вращающие моменты. К сожалению, при этом приходится пожертвовать основным достоинством эвольвентных зацеплений – качением профилей зубьев друг по другу и соответственно получить высокое трение в зубьях. Однако для тихоходных машин это не так важно.
В ней зубья каждого колеса имеют вогнутые ножки и выпуклые головки. Передачи с двумя линиями зацепления обладают большей несущей способностью, менее чувствительны к смещению осей, работают с меньшим шумом и более технологичны. Эти передачи успешно применяются при малых числах зубьев (Z1 < 10) и дают достаточную жёсткость шестерён при их большой относительной ширине. Зацепления Новикова в редукторах применяют вместо перехода на колёса с твёрдыми поверхностями. Расчёт передач Новикова на контактную прочность проводят на основе формулы Герца-Беляева, учитывая экспериментально установленный факт, что несущая способность передач при прочих равных условиях обратно пропорциональна синусу угла наклона зубьев. Кроме того, в расчёте немного завышаются допускаемые напряжения. Передачи бывают однопарные, применяемые в редукторах общего назначения и многопарные, получаемые за счёт увеличения осевого размера и применяемые в прокатных станах, редукторах турбин и т.п.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.251.22 (0.008 с.) |

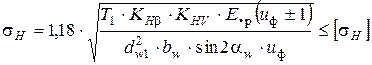 ;
;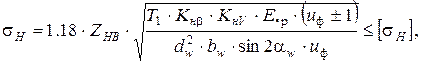
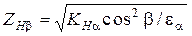 .
.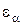 - коэффициент торцового перекрытия зубчатой передачи по формуле [1]:
- коэффициент торцового перекрытия зубчатой передачи по формуле [1]:
 ,
, необходимо по табл. 2.6 назначить степень точности передачи в зависимости от окружной скорости в зацеплении
необходимо по табл. 2.6 назначить степень точности передачи в зависимости от окружной скорости в зацеплении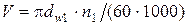 , м/с.
, м/с.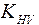 для рассчитываемой передачи.
для рассчитываемой передачи.
 .
.
 ,
,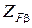 - коэффициент повышения прочности косозубых передач по напряжениям изгиба,
- коэффициент повышения прочности косозубых передач по напряжениям изгиба,  . Здесь Y -коэффициент, учитывающий повышение изгибной прочности вследствие наклона контактной линии на зубе к основанию зуба,
. Здесь Y -коэффициент, учитывающий повышение изгибной прочности вследствие наклона контактной линии на зубе к основанию зуба,  , где b подставляют в градусах. Коэффициент неравномерности распределения нагрузки между одновременно зацепляющимися зубьями KF назначают по табл. 2.8.
, где b подставляют в градусах. Коэффициент неравномерности распределения нагрузки между одновременно зацепляющимися зубьями KF назначают по табл. 2.8.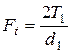 , Н.
, Н.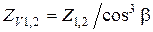 - для косозубых колес. Табл. 2.9 составлена для случая отсутствия смещения зуборезного инструмента (x=0) при зубонарезании.
- для косозубых колес. Табл. 2.9 составлена для случая отсутствия смещения зуборезного инструмента (x=0) при зубонарезании. в зубьях колёс оказываются значительно меньшей величины, чем допускаемые напряжения
в зубьях колёс оказываются значительно меньшей величины, чем допускаемые напряжения 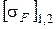 , то для закрытых передач это вполне допустимо, так как нагрузочная способность таких передач ограничивается, как правило, контактной выносливостью зубьев.
, то для закрытых передач это вполне допустимо, так как нагрузочная способность таких передач ограничивается, как правило, контактной выносливостью зубьев.

 - число зубьев шестерни открытой передачи (см. исходные данные);
- число зубьев шестерни открытой передачи (см. исходные данные);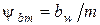 - коэффициент ширины зубчатого венца колеса относительно модуля, рекомендуют назначать для открытых передач bm = 10...15;
- коэффициент ширины зубчатого венца колеса относительно модуля, рекомендуют назначать для открытых передач bm = 10...15;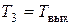 ;
;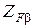 - определяют по п.2.5. («Проверка прочности зубьев по напряжениям изгиба»);
- определяют по п.2.5. («Проверка прочности зубьев по напряжениям изгиба»); или
или 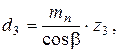


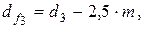


 Представляют собой цилиндрические передачи, где одно из колёс имеет гибкий венец. Этот гибкий венец деформируется генератором волн специальной некруглой формы и входит в зацепление с центральным колесом в двух зонах [17].
Представляют собой цилиндрические передачи, где одно из колёс имеет гибкий венец. Этот гибкий венец деформируется генератором волн специальной некруглой формы и входит в зацепление с центральным колесом в двух зонах [17]. Принцип работы волновой передачи аналогичен работе планетарной передачи с внутренним зацеплением и деформируемым сателлитом.
Принцип работы волновой передачи аналогичен работе планетарной передачи с внутренним зацеплением и деформируемым сателлитом. ;
;  ,
, Решая проблемы проектирования тяжёлых тихоходных машин, таких как трактора и танки, М.Л. Новиков в 1954 году разработал зацепления, в которых выпуклые зубья шестерни зацепляются с вогнутыми зубьями колеса.
Решая проблемы проектирования тяжёлых тихоходных машин, таких как трактора и танки, М.Л. Новиков в 1954 году разработал зацепления, в которых выпуклые зубья шестерни зацепляются с вогнутыми зубьями колеса. Рабочие боковые поверхности зубьев представляют собой круговинтовые поверхности, поэтому передачи можно называть круговинтовыми. В дальнейшем был разработан вариант передачи с двумя линиями зацепления.
Рабочие боковые поверхности зубьев представляют собой круговинтовые поверхности, поэтому передачи можно называть круговинтовыми. В дальнейшем был разработан вариант передачи с двумя линиями зацепления.


