
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные принципы и этапы разработки машинСодержание книги
Поиск на нашем сайте
ДЕТАЛИ МАШИН И ОСНОВЫ КОНСТРУИРОВАНИЯ
Конспект лекций
ВВЕДЕНИЕ
Современное общество отличается от первобытного использованием машин. Применение предметов, усиливающих возможности рук (палки, камни), и особенно освоение дополнительных источников энергии (костёр, лошадь) не только позволило человечеству выжить, но и обеспечило в дальнейшем победу над превосходящими силами природы. Жизнь людей, даже самых отсталых племён, теперь немыслима без различных механических устройств и приспособлений (греч. "механа" – хитрость).
С тех же пор наметились основные закономерности устройства и функционирования механизмов и машин, сложились наиболее рациональные и удобные формы их составных частей - деталей. В процессе механизации производства и транспорта, по мере увеличения нагрузок и сложности конструкций, возросла потребность не только в интуитивном, но и в научном подходе к созданию и эксплуатации машин. В ведущих университетах Запада уже с 30-х годов XIX века, а в Санкт-Петербургском университете с 1892 года читается самостоятельный курс "Детали Машин". Без этого курса [9,16,18,22,23,32] теперь невозможна подготовка инженера-механика любой специальности. Исторически сложившиеся в мире системы подготовки инженеров при всех национальных и отраслевых различиях имеют единую четырёхступенчатую структуру: 1. На младших курсах изучаются ФУНДАМЕНТАЛЬНЫЕ НАУКИ, которые представляют собой системы знаний о наиболее общих законах и принципах нашего мира. Это - Физика, Химия, Математика, Информатика, Теоретическая механика, Философия, Политология, Психология, Экономика, История и т.п. 2. Далее изучаются ПРИКЛАДНЫЕ НАУКИ, которые изучают действие фундаментальных законов природы в частных областях жизни, таковыми являются Техническая термодинамика, Теория прочности, Материаловедение, Сопротивление материалов, Теория механизмов и машин, Прикладная механика, Вычислительная техника и т.п.
3. На старших курсах (3-й и выше) студенты приступают к изучению ОБЩЕТЕХНИЧЕСКИХ ДИСЦИПЛИН, таких как НАШ КУРС, а также "Основы стандартизации", "Технология обработки материалов" и т.п.; отраслевые различия здесь ещё сравнительно невелики. 4. Обучение завершается освоением СПЕЦИАЛЬНЫХ ДИСЦИПЛИН, которые и составляют квалификацию инженера соответствующей специальности. При этом подлинно высококвалифицированным специалистом, способным решать конкретные инженерно-технические проблемы становится лишь тот, кто усвоит взаимосвязь и преемственность между фундаментальными, прикладными, общетехническими и специальными знаниями. Курс "Детали машин и основы конструирования" непосредственно опирается на курсы "Сопротивление материалов" и "Теория механизмов и машин", которыми, мы надеемся, студенты овладели в совершенстве. Кроме того, для успешного выполнения расчётно-графических работ и курсового проекта необходимы хорошие знания правил и приёмов курса "Инженерная графика". ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ КУРСА
Определим базовые понятия [21] в самом начале работы для систематизации учебного материала и во избежание двусмысленного толкования. Расположим понятия по степени сложности. ДЕТАЛЬ – (франц. detail – кусочек) – изделие, изготовленное из однородного по наименованию и марке материала без применения сборочных операций (ГОСТ 2.101-68). ЗВЕНО – группа деталей, образующая подвижную или неподвижную относительно друг друга механическую систему тел. СБОРОЧНАЯ ЕДИНИЦА – изделие, составные части которого подлежат соединению на предприятии-изготовителе посредством сборочных операций (ГОСТ 2.101-68). УЗЕЛ – законченная сборочная единица, состоящая из деталей общего функционального назначения. МЕХАНИЗМ – система деталей, предназначенная для передачи и преобразования движения. АППАРАТ – (лат. apparatus – часть) прибор, техническое устройство, приспособление, обычно некая автономно-функциональная часть более сложной системы. АГРЕГАТ – (лат. aggrego – присоединять) унифицированный функциональный узел, обладающий полной взаимозаменяемостью.
МАШИНА – (греч. "махина" – огромная, грозная) система деталей, совершающая механическое движение для преобразования энергии, материалов или информации с целью облегчения труда. Машина характерна наличием источника энергии и требует присутствия оператора для своего управления. Проницательный немецкий экономист К. Маркс заметил, что всякая машина состоит из двигательного, передаточного и исполнительного механизмов. АВТОМАТ – (греч. "аутомотос" – самодвижущийся) машина, работающая по заданной программе без оператора. РОБОТ – (чешск. robot – работник) машина, имеющая систему управления, позволяющую ей самостоятельно принимать исполнительские решения в заданном диапазоне. Процесс разработки машин имеет сложную, разветвлённую неоднозначную структуру и обычно называется широким термином ПРОЕКТИРОВАНИЕ – создание прообраза объекта, представляющего в общих чертах его основные параметры. Под КОНСТРУИРОВАНИЕМ некоторые авторы понимают весь процесс от идеи до изготовления машин, некоторые – лишь завершающую стадию его подготовки [14, 24, 25, 38]. Но в любом случае цель и конечный результат конструирования – создание рабочей документации (ГОСТ 2.102-68), по которой можно без участия разработчика изготавливать, эксплуатировать, контролировать и ремонтировать изделие. Здесь также требуется дать базовые понятия: ТЕХНИЧЕСКОЕ ЗАДАНИЕ – документ, составляемый совместно заказчиком и разработчиком, содержащий общее представление о назначении, технических характеристиках и принципиальном устройстве будущего изделия. ТЕХНИЧЕСКОЕ ПРЕДЛОЖЕНИЕ – дополнительные или уточнённые требования к изделию, которые не могли быть указаны в техническом задании (ГОСТ 2.118-73). ТВОРЧЕСТВО – специфическая материальная или духовная деятельность, порождающая нечто новое или новую комбинацию известного. ИЗОБРЕТЕНИЕ – новое решение технической задачи, дающее положительный эффект. ЭСКИЗИРОВАНИЕ – процесс создания эскиза (франц. es quisse – из размышлений), предварительного рисунка или наброска, фиксирующего замысел и содержащего основные очертания создаваемого объекта. КОМПОНОВКА – расположение основных деталей, узлов, сборочных единиц будущего объекта. РАСЧЁТ – численное определение усилий, напряжений и деформаций в деталях, установление условий их нормальной работы; выполняется по мере необходимости на каждом этапе конструирования. ЧЕРТЁЖ – точное графическое изображение объекта, содержащее полную информацию об его форме, размерах и основных технических условиях изготовления. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА – текстовый документ (ГОСТ 2.102-68), содержащий описание устройства и принципа действия изделия, а также технические характеристики, экономическое обоснование, расчёты, указания по подготовке изделия к эксплуатации. СПЕЦИФИКАЦИЯ – текстовый табличный документ, определяющий состав изделия (ГОСТ 2.102-68). ЭСКИЗНЫЙ ПРОЕКТ – первый этап проектирования (ГОСТ 2.119-73), когда устанавливаются принципиальные конструктивные и схемные решения, дающие общие представления об устройстве и работе изделия. ТЕХНИЧЕСКИЙ ПРОЕКТ – заключительный этап проектирования (ГОСТ 2.120-73), когда выявляются окончательные технические решения, дающие полное представление об изделии. РАБОЧИЙ ПРОЕКТ – полный комплект рабочей документации (текстовой и графической ГОСТ 2.102-68; 2.106-68), в которой содержится полная информация о конструкции, изготовлении, эксплуатации и ремонте машины.
Требования к машинам и критерии их качества
Поскольку человеку свойственно хотеть всего и сразу, то требования к машинам многообразны и часто противоречивы, однако их можно условно разделить на основные взаимосвязанные группы: è технологические требования; è экономические требования; è эксплуатационные требования. Качество машины, т.е. её максимальное соответствие всем требованиям [19, 37] невозможно без неустанного внимания инженера на всех стадиях "жизни" машины. Качество закладывается на стадии проектирования, обеспечивается на стадии производства и поддерживается в процессе эксплуатации. Степень соответствия требованиям характеризуют критерии качества (греч. "крит эрион" – узкое место) – некие конкретные параметры (греч. "пара мэтрос" – измеряемый), т.е. измеряемые или вычисляемые величины. Однако известно, что полное удовлетворение всех требований – абсолютно невыполнимая задача, поэтому всегда приходится идти на компромисс, обозначая главные требования и обеспечивая соответствующие им критерии качества. Отметим поэтому лишь основные требования к деталям и машинам. ТЕХНОЛОГИЧНОСТЬ – изготовление изделия при минимальных затратах труда, времени и средств при полном соответствии своему назначению. ЭКОНОМИЧНОСТЬ – минимальная стоимость производства и эксплуатации. РАБОТОСПОСОБНОСТЬ – состояние объекта, при котором он способен выполнять заданные функции. НАДЁЖНОСТЬ – свойство объекта сохранять во времени способность к выполнению заданных функций (ГОСТ 27.002-83).
Основными критериями качества машин считают:
МОЩНОСТЬ – скорость преобразования энергии; ПРОИЗВОДИТЕЛЬНОСТЬ – объём работы (продукции, информации), выполняемой в единицу времени; КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ – доля дошедшей до потребителя энергии (мощности); ГАБАРИТЫ – предельные размеры; ЭНЕРГОЁМКОСТЬ - расход топлива или электричества отнесённый к объёму работы (пройденному расстоянию, произведённой продукции); МАТЕРИАЛОЁМКОСТЬ – количество конструкционного материала машины, обычно отнесённого к единице мощности; ТОЧНОСТЬ – способность максимально соответствовать заданному положению (скорости и т.п.); ПЛАВНОСТЬ ХОДА – минимальные ускорения при работе машины.
КЛАССИФИКАЦИЯ ДЕТАЛЕЙ МАШИН
Не существует абсолютной, полной и завершённой классификации всех существующих деталей машин, т.к. конструкции их многообразны и, к тому же, постоянно разрабатываются новые. Для ориентирования в бесконечном многообразии детали машин классифицируют на типовые группы по характеру их использования [1,10,11]. è ПЕРЕДАЧИ передают движение от источника к потребителю. è ВАЛЫ и ОСИ несут на себе вращающиеся детали передач. è ОПОРЫ служат для установки валов и осей. è МУФТЫ соединяют между собой валы и передают вращающий момент. è СОЕДИНИТЕЛЬНЫЕ ДЕТАЛИ (СОЕДИНЕНИЯ) соединяют детали между собой. è УПРУГИЕ ЭЛЕМЕНТЫ смягчают вибрацию и удары, накапливают энергию, обеспечивают постоянное сжатие деталей. è КОРПУСНЫЕ ДЕТАЛИ организуют внутри себя пространство для размещения всех остальных деталей, обеспечивают их защиту. Рамки учебного курса не позволяют изучить все разновидности деталей машин и все нюансы проектирования. Однако знание, по крайней мере, типовых деталей и общих принципов конструирования машин даёт инженеру надёжный фундамент и мощный инструмент для выполнения проектных работ практически любой сложности. В следующих главах мы рассмотрим приёмы расчёта и проектирования типовых деталей машин.
КОНТРОЛЬНЫЕ ВОПРОСЫ s Каковы место и роль машин в современном обществе? s Какие учебные дисциплины непосредственно служат базой для курса "Детали машин и основы конструирования"? s В чём заключается разница между проектированием и конструированием? s Какие правила и нормы регламентируются Единой Системой Конструкторской Документации? s Кем формулируется и составляется Техническое Задание? s Какие документы являются результатом конструирования? s Какие группы требований предъявляются к машинам? s Каковы основные требования к деталям и машинам? s Каковы основные критерии качества деталей и машин? s Что такое работоспособность и каковы её критерии? s Что такое надёжность и каковы её критерии? s Что является главнейшим критерием работоспособности и надёжности? s В чём заключается общее условие прочности деталей машин? s В чём разница между проектировочным и проверочным расчётами? s Каковы основные группы деталей машин общего назначения?
ПЕРЕДАЧИ
Современные машины приводятся в движение главным образом топливными и электрическими двигателями. В силу специфики законов термогазодинамики и электромагнетизма, эти двигатели более быстроходны, чем было бы удобно для человека, к тому же их скорость сложно и плохо регулируется. Возникает необходимость согласования режимов работы двигателя и исполнительного органа [6,10], с которым, собственно, и имеет дело оператор. Для этого созданы передачи. Механическими передачами или просто передачами называются механизмы, которые преобразуют параметры движения от двигателя к исполнительным органам машины [1,10]. Механическая энергия передаётся, как правило, с преобразованием скоростей и вращающих моментов, а иногда с преобразованием вида и закона движения.
Передачи по принципу работы разделяются на: è Передачи зацеплением: è с непосредственным контактом (зубчатые и червячные); è с гибкой связью (цепные, зубчато-ременные). è Передачи трением (сцеплением трущихся поверхностей): è с непосредственным контактом поверхностей (фрикционные); è с гибкой связью (ременные).
ПЕРЕДАЧИ ЗАЦЕПЛЕНИЕМ
Передают движение с помощью последовательно зацепляющихся зубьев [1]. Силы в зубчатом зацеплении
Однако этот интеграл вычислить практически невозможно, т.к. неизвестен точный вид функции s к. Используют другой приём: ещё неизвестную силу нормального давления Fn сначала раскладывают на три ортогональных проекции: è осевую силу Fa, направленную параллельно оси колеса; è радиальную силу Fr, направленную по радиусу к центру колеса; è окружную силу Ft, направленную касательно к делительной окружности. Легче всего вычислить силу Ft, зная передаваемый вращающий момент Мвр и делительный диаметр dw Ft = 2MВр / dw. Радиальная сила вычисляется, зная угол зацепления aw Fr = Ft tgaw. Осевая сила вычисляется через окружную силу и угол наклона зубьев b Fa = Ft tgb. Наконец, если необходимо, зная все проекции, можно вычислить и модуль нормальной силы Fn= ( Fa2 + Fr2 + Ft2 ) ½ = Ft / ( cosαw cosβ ). Нормальная сила распределена по длине контактной линии, поэтому, зная длину lS контактной линии,можно вычислить удельную погонную нормальную нагрузку qn = Fn / lΣ ≈ Ft / ( b εαkε cosαw cosβ ), где e a - коэффициент перекрытия, k e - отношение минимальной длины контактной линии к средней. Для двух цилиндрических колёс в зацеплении одноимённые силы равны, но противоположны. Окружная сила для шестерни противоположна направлению вращения, окружная сила для колеса направлена в сторону вращения. Расчёт зубьев на контактную выносливость
Здесь Епр – приведённый модуль упругости материалов шестерни и колеса Епр = 2 Е1 Е2 / ( Е1 + Е2 ), rпр – приведённый радиус кривизны зубьев 1/rпр = 1/r1 ± 1/r2, r1,2 = 0,5dW 1,2 sin aW , n - коэффициент Пуассона, qn - удельная погонная нормальная нагрузка, [ s ] HE - допускаемые контактные напряжения с учётом фактических условий работы. Расчёт зубьев на контактную выносливость для закрытых передач (длительно работают на постоянных режимах без перегрузок) выполняют как проектировочный. В расчёте задаются передаточным отношением, которое зависит от делительных диаметров и определяют межосевое расстояние Аw (или модуль m), а через него и все геометрические параметры зубьев. Для открытых передач контактные дефекты не характерны и этот расчёт выполняют, как проверочный, вычисляя контактные напряжения и сравнивая их с допускаемыми.
Расчёт зубьев на изгиб
Зуб представляют как консольную балку переменного сечения, нагруженную окружной и радиальной силами (изгибом от осевой силы пренебрегают). При этом окружная сила стремится изогнуть зуб, вызывая максимальные напряжения изгиба в опасном корневом сечении, а радиальная сила сжимает зуб, немного облегчая его напряжённое состояние. sA = sизг А - sсжатия А. Напряжения сжатия вычитаются из напряжений изгиба. Учитывая, что напряжения изгиба в консольной балке равны частному от деления изгибающего момента Mизг на момент сопротивления корневого сечения зуба W, а напряжения сжатия это сила Fr, делённая на площадь корневого сечения зуба, получаем:
Здесь b – ширина зуба, m – модуль зацепления, YH – коэффициент прочности зуба. Иногда используют понятие коэффициента формы зуба YFH = 1 / YH. Таким образом, получаем в окончательном виде условие прочности зуба на изгиб: sA = qn YH / m ≤ [s]FE. Полученное уравнение решают, задавшись свойствами выбранного материала. Допускаемые напряжения на изгиб (индекс F) и контактные (индекс H) зависят от свойств материала, направления приложенной нагрузки и числа циклов наработки передачи [s]FE = [s]F KF KFC / SF; [s]HE = [s]H KH / SH. Здесь [s]F и [s ]H – соответственно пределы изгибной и контактной выносливости; SF и SH – коэффициенты безопасности, зависящие от термообработки материалов; KFC учитывает влияние двухстороннего приложения нагрузки для реверсивных передач; KF и KH - коэффициенты долговечности, зависящие от соотношения фактического и базового числа циклов наработки. Фактическое число циклов наработки находится произведением частоты вращения колеса и срока его службы в минутах. Базовые числа циклов напряжений зависят от материала и термообработки зубьев. Расчёт зубьев на изгиб для открытых передач (работают на неравномерных режимах с перегрузками) выполняют, как проектировочный. В расчёте задаются прочностными характеристиками материала и определяют модуль m, а через него и все геометрические параметры зубьев. Для закрытых передач излом зуба не характерен и этот расчёт выполняют, как проверочный, сравнивая изгибные напряжения с допускаемыми [42]. РАСЧЕТЫ ЗУБЧАТЫХ ПЕРЕДАЧ ПЛАНЕТАРНЫЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ Планетарными называют передачи, имеющие зубчатые колёса с перемещающимися осями [8,29]. Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение, называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси.
Планетарные передачи имеют ряд преимуществ перед обычными: + большие передаточные отношения при малых габаритах и массе; + возможность сложения или разложения механической мощности; + лёгкое управление и регулирование скорости; + малый шум вследствие замыкания сил в механизме. В планетарных передачах широко применяют внутреннее зубчатое зацепление с углом aw = 30о. Для обеспечения сборки планетарных передач необходимо соблюдать условие соосности (совпадение геометрических центров колёс); условие сборки (сумма зубьев центральных колёс кратна числу сателлитов) и соседства (вершины зубьев сателлитов не соприкасаются друг с другом). Зубчатые колёса планетарных передач рассчитываются по тем же законам, что и колёса обычных цилиндрических передач [39]. ВОЛНОВЫЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
Идея волновых передач заключается в наличии нескольких пар зацепления, которые ещё и перемещаются по окружности, за счёт чего достигается огромное передаточное отношение (обычно U60 ¸ 300, известны конструкции с U > 1000). И это в одной ступени!
Такая передача была запатентована американским инженером Массером в 1959 г. Волновые передачи имеют меньшие массу и габариты, большую кинематическую точность, меньший мёртвый ход, высокую вибропрочность за счёт демпфирования (рассеяния энергии) колебаний, создают меньший шум. При необходимости такие передачи позволяют передавать движение в герметичное пространство без применения уплотняющих сальников, что особенно ценно для авиационной, космической и подводной техники, а также для машин химической промышленности.
К недостаткам волновых передач относятся: ` ограниченные обороты ведущего вала (во избежание больших центробежных сил инерции некруглого генератора волн); ` мелкие модули зубьев (1,5 – 2 мм); ` практически индивидуальное, дорогостоящее, весьма трудоёмкое изготовление гибкого колеса и генератора.
Основные виды поломок волновых передач: · разрушение подшипника генератора волн от нагрузки в зацеплении; · проскакивание генератора волн при больших вращающих моментах, когда зубья на входе в зацепление упираются друг в друга вершинами; · поломка гибкого колеса от трещин усталости (особенно при U < 80); · износ зубьев на концах; · пластические деформации боковых поверхностей зубьев при перегрузках. Расчёт волновых зубчатых передач отличается от расчёта обычных зубчатых передач тем, что учитывается деформация гибкого венца и генератора [40]. За критерий работоспособности обычно принимают допускаемые напряжения смятия где Yd – коэффициент ширины гибкого венца; d – делительный диаметр гибкого венца.
ЗАЦЕПЛЕНИЯ НОВИКОВА
Итак, основной недостаток зубчатых передач с эвольвентным профилем (цилиндрических, конических, планетарных, волновых) – высокие контактные напряжения в зубьях. Они велики потому, что контактируют два зуба с выпуклыми профилями. При этом площадка контакта очень мала, а контактные напряжения соответственно высоки. Это обстоятельство сильно ограничивает "несущую способность" передач, т.е. не позволяет передавать большие вращающие моменты.
К тому же выпуклый и вогнутый профили (обычно круговые) имеют близкие по абсолютной величине радиусы кривизны. За счёт этого получается большая площадка контакта, контактные напряжения уменьшаются и появляется возможность передавать примерно в 1,4 ¸ 1,8 раза большие вращающие моменты. К сожалению, при этом приходится пожертвовать основным достоинством эвольвентных зацеплений – качением профилей зубьев друг по другу и соответственно получить высокое трение в зубьях. Однако для тихоходных машин это не так важно.
В ней зубья каждого колеса имеют вогнутые ножки и выпуклые головки. Передачи с двумя линиями зацепления обладают большей несущей способностью, менее чувствительны к смещению осей, работают с меньшим шумом и более технологичны. Эти передачи успешно применяются при малых числах зубьев (Z1 < 10) и дают достаточную жёсткость шестерён при их большой относительной ширине. Зацепления Новикова в редукторах применяют вместо перехода на колёса с твёрдыми поверхностями. Расчёт передач Новикова на контактную прочность проводят на основе формулы Герца-Беляева, учитывая экспериментально установленный факт, что несущая способность передач при прочих равных условиях обратно пропорциональна синусу угла наклона зубьев. Кроме того, в расчёте немного завышаются допускаемые напряжения. Передачи бывают однопарные, применяемые в редукторах общего назначения и многопарные, получаемые за счёт увеличения осевого размера и применяемые в прокатных станах, редукторах турбин и т.п. ФРИКЦИОННЫЕ ПЕРЕДАЧИ Передают движение за счёт сил трения (лат. frictio – трение). Простейшие передачи состоят из двух цилиндрических или конических роликов - катков.
Передаточное отношение цилиндрической фрикционной передачи определяют как отношение частот вращения или диаметров тел качения.
U = n1/n2=D2 /[ D1 ( 1-e )], где ε – коэффициент скольжения (0,05 - для передач "всухую"; 0,01 – для передач со смазкой и большими передаточными отношениями). Для конической передачи – вместо диаметров берут углы конусов. Фрикционные передачи выполняются либо с постоянным, либо с регулируемым передаточным отношением (вариаторы). Передачи с постоянным передаточным отношением применяются редко, главным образом, в кинематических цепях приборов, например, магнитофонов и т.п. Они уступают зубчатым передачам в несущей способности. Зато фрикционные вариаторы применяют как в кинематических, так и в силовых передачах для бесступенчатого регулирования скорости. Зубчатые передачи не позволяют такого регулирования.
Достоинства фрикционных передач: + простота тел качения; + равномерность вращения, что удобно для приборов; + возможность плавного регулирования скорости; + отсутствие мёртвого хода при реверсе передачи. Недостатки фрикционных передач: ` потребность в прижимных устройствах; ` большие нагрузки на валы, т.к. необходимо прижатие дисков; ` большие потери на трение; ` повреждение катков при пробуксовке; ` неточность передаточных отношений из-за пробуксовки. Основными видами поломок фрикционных передач являются: r усталостное выкрашивание (в передачах с жидкостным трением смазки, когда износ сводится к минимуму); r износ (в передачах без смазки); r задир поверхности при пробуксовке.
Поскольку всё это следствие высоких контактных напряжений сжатия, то в качестве проектировочного выполняется расчёт по допускаемым контактным напряжениям [29]. Здесь применяется формула Герца-Беляева, которая, собственно говоря, и была выведена для этого случая. Исходя из допускаемых контактных напряжений, свойств материала и передаваемой мощности определяются диаметры фрикционных колёс
Основные требования к материалам фрикционных колёс: è высокая износостойкость и поверхностная прочность; è высокий коэффициент трения (во избежание больших сил сжатия); è высокий модуль упругости (чтобы площадка контакта, а значит и потери на трение были малы). Наиболее пригодными оказываются шарикоподшипниковые стали типа ШХ15 или 18ХГТ, 18Х2Н4МА. Разработаны специальные фрикционные пластмассы с асбестовым и целлюлозным наполнителем, коэффициент трения которых достигает 0,5. Широко применяется текстолит. Более надёжны передачи, у которых ведущий каток твёрже, чем ведомый, т.к. тогда при пробуксовке не образуются лыски. Применяются обрезиненные катки, однако их коэффициент трения падает с ростом влажности воздуха. Для крупных передач применяют прессованный асбест, прорезиненную ткань и кожу.
РЕМЕННЫЕ ПЕРЕДАЧИ
Ременные передачи применяются для привода агрегатов от электродвигателей малой и средней мощности; для привода от маломощных двигателей внутреннего сгорания. Ремни имеют различные сечения:
б) трапециевидные, клиновые; в) круглого сечения; г) поликлиновые. Наибольшее распространение имеют плоские и клиновые ремни. Плоские ремни применяются как простейшие, с минимальными напряжениями изгиба, а клиновые имеют повышенную тяговую способность. Клиновые ремни применяют по несколько штук, чтобы варьировать нагрузочную способность и несколько повысить надёжность передачи. Кроме того, один толстый ремень, поставленный вместо нескольких тонких будет иметь гораздо большие напряжения изгиба при огибании шкива. В лёгких передачах благодаря закручиванию ремня можно передавать вращение между параллельными, пересекающимися, вращающимися в противоположные стороны валами. Это возможно потому, что жёсткость на кручение ремней вследствие их малой толщины и малого модуля упругости мала. Достоинства ременных передач: + передача движения на средние расстояния; + плавность работы и бесшумность; + возможность работы при высоких оборотах; + дешевизна.
Недостатки ременных передач: ` большие габариты передачи; ` неизбежное проскальзывание ремня; ` высокие нагрузки на валы и опоры из-за натяжения ремня; ` потребность в натяжных устройствах; ` опасность попадания масла на ремень; ` малая долговечность при больших скоростях. Основные критерии расчёта ременных передач: è тяговая способность или прочность сцепления ремня со шкивом; è долговечность ремня. Если не будет выдержано первое условие, ремень начнёт буксовать, если не выполнить второе – ремень быстро разорвётся. Поэтому основным расчётом ременных передач является расчёт по тяговой способности. Расчёт на долговечность выполняется, как проверочный [24,25,29].
Общая длина ремня не зависит от нагрузки [16], следовательно, суммарное натяжение ветвей остаётся постоянным: F1 + F2 = 2Fo. Таким образом, получаем систему двух уравнений c тремя неизвестными:
Эти уравнения устанавливают изменение натяжения ветвей в зависимости от нагрузки Ft, но не показывают нам тяговую способность передачи, которая связана с силой трения между ремнём и шкивом. Такая связь установлена Л.Эйлером с помощью дифференциального анализа.
rF + rfdR – r ( F + dF ) = 0. Сумма горизонтальных проекций сил: dR – Fsin ( dφ/2 ) – ( F+dF ) sin ( dφ/2 ) = 0. Отбрасывая члены второго порядка малости и помня, что синус бесконечно малого угла равен самому углу, Эйлер получил простейшее дифференциальное уравнение: dF/F = f dφ. Интегрируя левую часть этого уравнения в пределах от F1 до F2, а правую часть в пределах угла обхвата ремня получаем: F1 = F2 e fα. Теперь стало возможным найти все неизвестные силы в ветвях ремня: F1 = Ft efα /( efα - 1); F2 = Ft /( efα - 1); Fo = Ft ( efα + 1)/ 2( efα - 1). Полученные формулы устанавливают
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.245.152 (0.021 с.) |

 И хотя различные механические хитрости использовались уже в древнем Египте при строительстве пирамид, всерьёз говорить о применении машин можно лишь с эпохи промышленной революции XVIII века, когда изобретение паровой машины дало гигантский технологический рывок и сформировало современный мир в его нынешнем виде. Здесь важен энергетический аспект проблемы.
И хотя различные механические хитрости использовались уже в древнем Египте при строительстве пирамид, всерьёз говорить о применении машин можно лишь с эпохи промышленной революции XVIII века, когда изобретение паровой машины дало гигантский технологический рывок и сформировало современный мир в его нынешнем виде. Здесь важен энергетический аспект проблемы. Фактически, движение передаётся зубчатым зацеплением посредством силы нормального давления в точке контакта зубьев Fn, которая определяется, как интеграл от контактных напряжений s к по всей площади S контакта зубьев Fn = ∫s ( s к )d S.
Фактически, движение передаётся зубчатым зацеплением посредством силы нормального давления в точке контакта зубьев Fn, которая определяется, как интеграл от контактных напряжений s к по всей площади S контакта зубьев Fn = ∫s ( s к )d S. Аналитическими методами теории прочности можно получить точное решение для вычисления напряжений в контакте двух эвольвентных профилей. Однако это слишком усложнит задачу, поэтому на малой площадке контакта геометрия эвольвентных профилей корректно подменяется контактом двух цилиндров. Для этого случая используют формулу Герца-Беляева:
Аналитическими методами теории прочности можно получить точное решение для вычисления напряжений в контакте двух эвольвентных профилей. Однако это слишком усложнит задачу, поэтому на малой площадке контакта геометрия эвольвентных профилей корректно подменяется контактом двух цилиндров. Для этого случая используют формулу Герца-Беляева: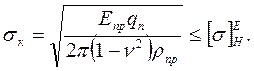


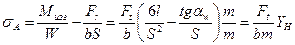 .
.
 Представляют собой цилиндрические передачи, где одно из колёс имеет гибкий венец. Этот гибкий венец деформируется генератором волн специальной некруглой формы и входит в зацепление с центральным колесом в двух зонах [17].
Представляют собой цилиндрические передачи, где одно из колёс имеет гибкий венец. Этот гибкий венец деформируется генератором волн специальной некруглой формы и входит в зацепление с центральным колесом в двух зонах [17]. Принцип работы волновой передачи аналогичен работе планетарной передачи с внутренним зацеплением и деформируемым сателлитом.
Принцип работы волновой передачи аналогичен работе планетарной передачи с внутренним зацеплением и деформируемым сателлитом. ;
;  ,
, Решая проблемы проектирования тяжёлых тихоходных машин, таких как трактора и танки, М.Л. Новиков в 1954 году разработал зацепления, в которых выпуклые зубья шестерни зацепляются с вогнутыми зубьями колеса.
Решая проблемы проектирования тяжёлых тихоходных машин, таких как трактора и танки, М.Л. Новиков в 1954 году разработал зацепления, в которых выпуклые зубья шестерни зацепляются с вогнутыми зубьями колеса. Рабочие боковые поверхности зубьев представляют собой круговинтовые поверхности, поэтому передачи можно называть круговинтовыми. В дальнейшем был разработан вариант передачи с двумя линиями зацепления.
Рабочие боковые поверхности зубьев представляют собой круговинтовые поверхности, поэтому передачи можно называть круговинтовыми. В дальнейшем был разработан вариант передачи с двумя линиями зацепления. Главное условие работы передачи состоит в том, что момент сил трения между катками должен быть больше передаваемого вращающего момента.
Главное условие работы передачи состоит в том, что момент сил трения между катками должен быть больше передаваемого вращающего момента.
 Являются разновидностью фрикционных передач, где движение передаётся посредством специального кольцевого замкнутого ремня.
Являются разновидностью фрикционных передач, где движение передаётся посредством специального кольцевого замкнутого ремня. а) плоские, прямоугольного сечения;
а) плоские, прямоугольного сечения;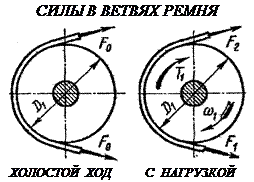 Для создания трения ремень надевают с предварительным натяжением Fo. В покое или на холостом ходу ветви ремня натянуты одинаково. При передаче вращающего момента Т1 натяжения в ветвях перераспределяются: ведущая ветвь натягивается до силы F1, а натяжение ведомой ветви уменьшается до F2. Составляя уравнение равновесия моментов относительно оси вращения имеем –T1 + F1D1/2 – F2D2/2 = 0 или F1 – F2 = Ft, где Ft – окружная сила на шкиве Ft = 2T1/D1.
Для создания трения ремень надевают с предварительным натяжением Fo. В покое или на холостом ходу ветви ремня натянуты одинаково. При передаче вращающего момента Т1 натяжения в ветвях перераспределяются: ведущая ветвь натягивается до силы F1, а натяжение ведомой ветви уменьшается до F2. Составляя уравнение равновесия моментов относительно оси вращения имеем –T1 + F1D1/2 – F2D2/2 = 0 или F1 – F2 = Ft, где Ft – окружная сила на шкиве Ft = 2T1/D1. F1 = Fo + Ft/2;
F1 = Fo + Ft/2;  Рассмотрим элементарный участок ремня dφ. Для него dR – нормальная реакция шкива на элемент ремня, fdR – элементарная сила трения. По условию равновесия суммы моментов
Рассмотрим элементарный участок ремня dφ. Для него dR – нормальная реакция шкива на элемент ремня, fdR – элементарная сила трения. По условию равновесия суммы моментов


