
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зацепление двух эвольвентных зубчатых колес.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Эвольвентой или разверткой окружности называют кривую АА1А2А3 (рис. 2, а), описываемую точкой А прямой АВ, лежащей в плоскости круга и перекатывающейся без скольжения по его окружности радиуса rb. Окружность диаметра db называют основной окружностью эвольвенты АА1А2А3….
 Эвольвенту можно получить еще и таким способом: к концу нерастяжимой нити, намотанной в один слой на боковую поверхность неподвижного кругового цилиндра, прикрепить острие карандаша и провести линию по листу бумаги, лежащему в плоскости разматывания нити и перпендикулярному оси цилиндра (рис. 2, б). Эвольвенту можно получить еще и таким способом: к концу нерастяжимой нити, намотанной в один слой на боковую поверхность неподвижного кругового цилиндра, прикрепить острие карандаша и провести линию по листу бумаги, лежащему в плоскости разматывания нити и перпендикулярному оси цилиндра (рис. 2, б).
Профилирование боковой поверхности зубьев по эвольвенте впервые было предложено математиком Леонардом Эйлером в 1754 г.
Эвольвентная система зацепления обеспечивает высокую прочность зубьев, простоту и удобство измерения параметров зацепления, взаимозаменяемость зубчатых колес при любых передаточных отношениях. На рис. 4 показано силовое давление Fn зуба шестерни 1 на зуб колеса 11.
Общая нормаль к сопряженным профилям зубьев делит межосевое расстояние на отрезки, обратно пропорциональные угловым скоростям. Если положение точки П, называемой полюсом зацепления, неизменно в любой момент зацепления, то передаточное отношение
Окружности, касающиеся друг друга в полюсе зацепления, имеющие общие с зубчатыми колесами центры и перекатывающиеся одна по другой без скольжения, называются начальными (рис. 3), их диаметры обозначают
 пары зубчатых колес меняются и положение полюса зацепления П на линии центров пары зубчатых колес меняются и положение полюса зацепления П на линии центров  , а следовательно, и размер начальных диаметров зубчатых колес, т.е. у пары сопряженных зубчатых колес может быть бесчисленное множество начальных окружностей. Заметим, что понятие «начальные окружности» относится лишь к паре сопряженных зубчатых колес; для каждого отдельно взятого зубчато колеса нельзя говорить о начальной окружности. , а следовательно, и размер начальных диаметров зубчатых колес, т.е. у пары сопряженных зубчатых колес может быть бесчисленное множество начальных окружностей. Заметим, что понятие «начальные окружности» относится лишь к паре сопряженных зубчатых колес; для каждого отдельно взятого зубчато колеса нельзя говорить о начальной окружности.
Если заменить одно из колес зубчатой рейкой (рис. 6), то для каждого зубчатого колеса найдется только одна окружность, катящаяся по начальной прямой CD рейки без скольжения; эта окружность называется делительной. В дальнейшем рассматриваются только такие зубчатые передачи, у которых начальные и делительные окружности совпадают.
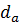 . Окружность, ограничивающую впадины зубьев, называют окружностью впадин зубчатого колеса; ее диаметр обозначают . Окружность, ограничивающую впадины зубьев, называют окружностью впадин зубчатого колеса; ее диаметр обозначают  . .
Часть профиля зуба, ограниченная делительной окружностью и окружностью выступов, называется головкой зуба; высоту головки зуба обозначают Между диаметрами основной и делительной окружностей существует зависимость
Прямая линия А1А2, проходящая через полюс зацепления П касательно основным окружностям шестерни (зубчатое колесо с меньшим числом зубьев) и колеса (зубчатое колесо с большим числом зубьев), называется линией зацепления. Линия зацепления является линией давления сопряженных профилей зубьев в процессе эксплуатации зубчатой передачи. Угол Угол профиля зуборезного инструмента
Отрезок Расстояние между одноименными профилями двух соседних зубьев, взятое по дуге делительной (основной) окружности, называется окружным шагом по делительной
Отношение длины зацепления к окружному шагу по основной окружности называется коэффициентом торцевого перекрытия:
Если коэффициент больше единицы, то до выхода из зацепления одной пары зубьев к линии зацепления подходит другая пара зубьев – это и обеспечивает непрерывность зацепления и плавность хода передачи. Чем больше коэффициент перекрытия, тем большее число пар зубьев одновременно находится в зацеплении. Так как длина делительной окружности равна произведению окружного (торцового) шага
где
|
|||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 Зубья, профиль которых очерчен эвольвентой (рис. 3), относительно легко, просто и точно могут быть нарезаны на зуборезных станках простейшим режущим инструментом – гребенкой (инструментальная рейка) с прямолинейными режущими кромками.
Зубья, профиль которых очерчен эвольвентой (рис. 3), относительно легко, просто и точно могут быть нарезаны на зуборезных станках простейшим режущим инструментом – гребенкой (инструментальная рейка) с прямолинейными режущими кромками.
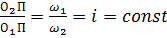 (1)
(1) Если положение полюса зацепления П будет изменяться на неизменном отрезке линии центров О1О2, то согласно формуле (1) передаточное отношение не будет постоянным.
Если положение полюса зацепления П будет изменяться на неизменном отрезке линии центров О1О2, то согласно формуле (1) передаточное отношение не будет постоянным. .
.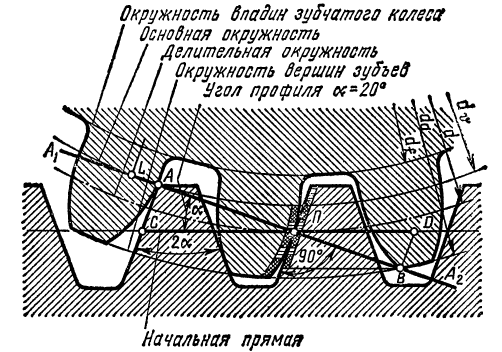 Так как у каждого зубчатого колеса имеется только одна делительная окружность, то она и положена в основу определения основных параметров зубчатой передачи; ее обозначают d (рис. 3).
Так как у каждого зубчатого колеса имеется только одна делительная окружность, то она и положена в основу определения основных параметров зубчатой передачи; ее обозначают d (рис. 3). . Часть профиля зуба, ограниченная делительной окружностью и окружностью впадин, называется ножкой зуба; высоту ножки зуба обозначают
. Часть профиля зуба, ограниченная делительной окружностью и окружностью впадин, называется ножкой зуба; высоту ножки зуба обозначают  . Высота зуба
. Высота зуба  /
/ (2)
(2)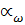 , образованный линией зацепления А1А2 и общей касательной, проведенной через полюс зацепления к делительным (начальным) окружностям шестерни и колеса, называется углом зацепления.
, образованный линией зацепления А1А2 и общей касательной, проведенной через полюс зацепления к делительным (начальным) окружностям шестерни и колеса, называется углом зацепления. равен 200. Следовательно,
равен 200. Следовательно,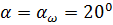
 линии зацепления, ограниченной окружностями выступов шестерни и колеса, называется активной частью линии зацепления или длиной зацепления. Длина зацепления определяет начало и конец зацепления пары сопряженных зубьев (рис. 3). Путь, проходимый точкой профиля зуба по делительной (начальной) окружности за время его фактического зацепления, называется дугой зацепления.
линии зацепления, ограниченной окружностями выступов шестерни и колеса, называется активной частью линии зацепления или длиной зацепления. Длина зацепления определяет начало и конец зацепления пары сопряженных зубьев (рис. 3). Путь, проходимый точкой профиля зуба по делительной (начальной) окружности за время его фактического зацепления, называется дугой зацепления. или основной
или основной  окружностям. Для сопряженной пары зубчатых колес шаг по делительной окружности шестерни и колеса одинаков и равен шагу производящей (инструментальной) рейки. Между шагами по делительной и основной окружностям существует зависимость:
окружностям. Для сопряженной пары зубчатых колес шаг по делительной окружности шестерни и колеса одинаков и равен шагу производящей (инструментальной) рейки. Между шагами по делительной и основной окружностям существует зависимость: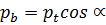 (3)
(3)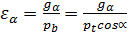 (4)
(4) , то
, то (5)
(5) - окружной модуль зубьев, являющийся основным параметром зубчатой передачи.
- окружной модуль зубьев, являющийся основным параметром зубчатой передачи.


