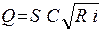Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Давление покоющийся жидкости на плоской пов-ти. ВыводСодержание книги
Поиск на нашем сайте
Билет №1 Давление покоющийся жидкости на плоской пов-ти.Вывод Одной из основных задач гидростатики является определение величины суммарной силы, действующей на плоскую поверхность со стороны покоящейся жидкости. Суммарная сила является вектором, и определение ее сведется к вычислению величины вектора, его направления и определению координат точки его приложения. Так как в каждой точке давление направлено по нормали к площадке, то и суммарная сила направлена по нормали.
F = р S где р – гидростатическое давление, S – величина площади. Решаемая ниже задача возникает по той простой причине, что в разных точках негоризонтальной стенки величина давления различная. Можно утверждать, что суммарная сила, действующая на любую площадку будет пропорциональна ее площади и будет иметь место формула вида (8.1); единственное, что необходимо при этом определить – в какой точке внутри площадки определяется давление р.
совмещения с плоскостью чертежа (т.е. на 90о). Тогда координатная ось Ох займет положение Ох1, ось Оz останется на месте, а площадка S изобразится на чертеже в натуральную величину. Представим площадку S состоящей из бесконечно малых частей dS. Рассмотрим одну из них, рис. 8.1. и допустим, что давление в ее центре равно р, тогда с точностью до бесконечно малых второго порядка можно записать для силы гидростатического давления, действующей на нее
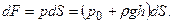
Всю силу F действующую на всю площадку S можно тогда записать в виде интеграла, т.е.
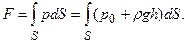
В последней формуле интеграл
равен статическому моменту площади S относительно координатной оси Ох1 (или Ох). Из теоретической механики известно, что статический момент некоторой площади S относительно заданной оси равен произведению площади S на расстояние от ее центра тяжести до оси. В данном случае
или, заменяя zc sina = hc, где hc – глубина погружения центра тяжести площади S под уровень свободной поверхности, получим выражение для силы полного (абсолютного) давления
 . .
или (так как rghc = рс)
где р с – гидростатическое давление в центре тяжести площадки. Таким образом, поставленная задача об определении величины силы решена. Билет №2 Особенности турбулентного режима(мгновенная и определённая скорости)Распределение скорости по сечению грубой трубы при этом режиме Схемы турбулентных потоков.
Вязкий слой расположен в непосредственной близости от стенки; в нём наблюдаются редкие турбулентные пульсации, но и они подавляются силами вязкости. Поэтому в весьма тонком вязком слое характер течения обуславливается в основном вязким трением. Средняя толщина вязкого слоя в такой схеме может быть больше или меньше средней высоты бугорков (выступов шероховатости стенок. На твердых и неподвижных стенках скорость равна нулю, а с удалением от них резко возрастает. В связи с этим получаются относительно большие градиенты скорости Толщина
где N-постоянная величина. В переходной области силы вязкого трения соизмеримы с движущими силами. Эта область располагается между вязким слоем и областью развитого турбулентного течения, называемой ядром турбулентного потока. Билет № 3 1)Последовательное и параллельное соединение простых трубопроводов(исходные уравнение и методы решения) Рассмотрим систему из последовательно соединенных труб различных диаметров и длин. Такое соединение участков трубопровода называется последовательным, рис. 4.1.
Рис.4.1. Рис.4.2.
H = H1 + H2 + H3 + …+ Hn, где H1, H2 , H3, …, Hn – потери напора на 1, 2, 3, …n-ом участке. Учитывая, что для каждого участка последовательного соединения справедлива зависимость (2.7) и имея в виду, что на каждом участке расход одинаковый, запишем (4.2) в виде:
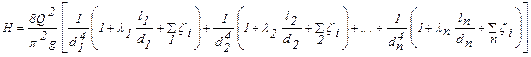 . .
Из (4.3) следует, что решение первой и второй задач при последовательном соединении участков трубопровода разного диаметра будет таким же как для простого трубопровода (трубопровода постоянного диаметра). Третья же задача, если в ней потребовать определения диаметров для всех участков, становится неопределенной, так как в этом случае уравнение (4.3) содержит n неизвестных. Для решения этой задачи необходимо задать диаметры труб для всех участков, кроме одного, который может быть тогда определен. Задача 4.1. Определить потери напора в стальном трубопроводе, состоящем из двух участков длиной l 1 = 120 м и l 2 = 250 м. Диаметры труб участков d 1 = 120 мм и d 2 = 100 мм. Расход воды в трубопроводе Q = 12,2 л/с, кинематический коэффициент вязкости воды принять равным n = 0,01 см2/с. Решение. В данном случае общие потери равны сумме потерь на каждом из участков. По справочнику определяем кЭ = 0,02 мм. Определяем последовательно для первого участка V1 =
Аналогично для второго участка V2 = 1,55 м/с; Re2 = 155414; Re2
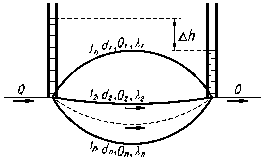
Ответ: общие потери напора равны 6,23 м. Параллельное соединение При параллельном соединении участков трубопровода жидкость, подходя с расходом Q к точке их разветвления А, распределяется по ответвлениям и далее снова собирается в точке их соединения В, рис. 4.2. При параллельном соединение обычно заданы o Суммарный расход до точки разветвления, o Длина, диаметр, величина кэ каждой ветви. Основными задачами гидравлического расчета в этом случае являются. o Определение расходов Q1, Q2, Q3, …, Qn, на отдельных участках, соединенным параллельно. o Определение потерь напора Δh между точками А и В, на каждом участке. При решении задачи прежде всего учтём очевидное условие: равенство расхода Q сумме всех расходов на отдельных участках
Δh = Δh 1 = Δh 2 = Δh 3 = …= Δh n Решая систему уравнений (4.5), можно выразить все расходы через один (например, через Q1) и подставив затем эти значения расходов в (4.4) найти Q1. после этого с помощью (4.5) определяют последовательно расходы Q2, Q3, …, Qn, а по любому из уравнений системы (4.5) определяют потери напора Н. Задача 4.2. Определить расходы и потери напора в каждой из n параллельно соединенных ветвей, считая, что как местные сопротивления, так и сопротивления по длине – в квадратичной области. Решение: В общем случае имеем для потерь в каждой ветви
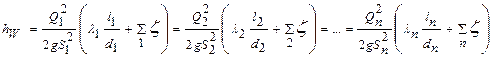
Имеем также
Примем обозначения
тогда уравнения (4.6) перейдут в такие
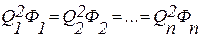
Из последнего уравнения выражаем все расходы через один, например через Q 1
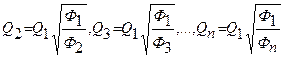
Затем из (4.7) получаем
Решая последнее уравнение относительно Q1, определим его значение, а из (4.9) и все остальные расходы; по любой из зависимостей (4.6) находим hW. Задача 4.3. Определить расходы и потери в каждой из трех ветвей параллельной сети, если длины и диаметры каждой из них равны соответственно l 1, l 2, l 3 и d 1, d 2, d 3. Известно, что местных сопротивлений нет, расход перед точкой разветвления равен Q, кинематический коэффициент вязкости n и то, что во всех трех ветвях движение ламинарное. Фазы гидравлического удара Рассмотрим фазы гидравлического удара при закрытии трубы, по которой жидкость вытекает из открытого резервуара. Пусть в конце горизонтальной трубы, по которой жидкость движется со скоростью V0, произведено мгновенное закрытие крана, рис.9.1.а. При этом скорость частиц жидкости, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдёт в работу деформации стенок трубы и жидкости (стенки растягиваются, а жидкость сжимается). На заторможенные частицы у крана набегают другие, соседние с ними и тоже теряют скорость; в результате сечения n-n перемещается влево со скоростью с, называемой скоростью ударной волны. Сама же переходная область, в которой давление изменяется на величину Δpуд, называется ударной волной.
Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы растянутыми. Ударное повышение давления Δpуд распространится на всю трубу, рис.9.1.б. Но такое состояние не является равновесным. Под действием перепада давления Δpуд частицы жидкости устремятся из трубы в резервуар, причём это движение начнётся с сечения, непосредственно прилегающего к резервуару. Теперь сечение n-n перемещается в обратном направлении – к крану – с той же скоростью с, оставляя за собой выровненное давление р0, рис.9.1.в. Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию, соответствующие давлению р0. Работа деформации полностью переходит в кинетическую энергию и жидкость в трубе приобретает первоначальную скорость V0, но направленную теперь в противоположную сторону. С этой скоростью «жидкая колонна», рис.9.1.г, стремится оторваться от крана, в результате возникает отрицательная ударная волна (P0 - ΔPуд), которая направлена от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость, что обусловлено снижением давления, рис.9.1д. Кинетическая энергия жидкости вновь переходит в работу деформаций, но противоположного знака. Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рис.9.1.е. Так же как для случая, изображённого на рис.9.1.б, оно не является равновесным. На рис.9.1.ж показан процесс выравнивания давления в трубе и в резервуаре, сопровождающийся возникновением движения жидкости со скоростью V0. Очевидно, что как только отражённая от резервуара ударная волна под давлением Δpуд достигает крана, возникает ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторился. После нескольких циклов из-за возникающего при движении трения Δpуд постепенно уменьшается, и энергия рассеивания. Формула Н.Е. Жуковского для Δpуд Для определения Δpуд применим второй закон Ньютона в виде
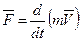 . .
 или или 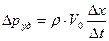 . Величина . Величина
Зависимость (9.4) носит название формулы Жуковского для величины превышения давления при гидравлическом ударе. Скорость распространения ударной волны с зависит от рода жидкости материала, диаметра, толщины стенок трубы и может быть найдена так
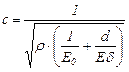
где ρ – плотность жидкости, Е0 – модуль упругости жидкости, d – внутренний диаметр трубы, Е – модуль упругости материала стенок трубы, δ – толщина стенок трубы. Для воды при обычных значениях отношения δ/d значения скорости с может приближённо приниматься равным 1200 м/с для стальных труб и 1000 м/с для чугунных. Формула (9.5) справедлива для так называемого прямого гидравлического удара. Гидравлическиё удар называется прямым, если время закрытия запорного устройства меньше времени двойного пробега ударной волны вдоль трубопровода При Гидравлический удар также может иметь место и при быстром открытии задвижки на напорном трубопроводе. В этом случае происходит значительное понижение давления в трубопроводе в результате резкого увеличения скорости. Такой гидравлический удар, характеризующийся понижением давления, носит название отрицательного удара. Билет №4 1)Основное уравнение для расчёта простого трубопровода(вывод) Простой трубопровод – это труба постоянного диаметра с местными сопротивлениями, по которой проходит постоянный расход. Большинство простых трубопроводов вписывается в одну из следующих двух схем, рис. 2.1.; в резервуарах уровень поддерживается постоянным и поэтому течение везде установившееся.
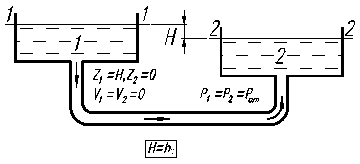
Схема 1 Схема 2 Рис.2. 1. В обоих случаях движущей силой является сила тяжести, которая приводит к разности давлений и под действием этой разности жидкость приходит в движение. В обоих случаях потенциальная энергия положения преобразуется в кинетическую энергию, а последняя – в тепловую за счет сил трения.
Точнее результат для скорости течения получается, если приравнять запас потенциальной энергии и кинетическую энергию текущей жидкости. Для случая идеальной жидкости
В действительности вследствие вязкости (трение в жидкости) часть кинетической энергии переходит в тепловую. Поэтому чем больше сопротивлений по длине и местных, тем скорость течения меньше. Как это часто бывает, наиболее точный и исчерпывающий результат получается при решении общих уравнений. В данном случае вполне понятно, что основным уравнением, связывающим запас потенциальной энергии, кинетическую энергию потока и потери является уравнение Бернулли
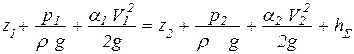
Суммарные потери hΣ складываются из потерь по длине hl и местных hм
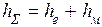 , ,
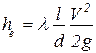
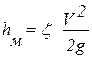 . .
Выбираем плоскость (ось) сравнения, совпадающей с осью горизонтальной части трубопровода, а сечения 1-1 и 2-2 совпадающими со свободными поверхностями в сосудах, рис. 2.1. Физический смысл уравнения для схемы 1 следующий: потенциальная энергия положения частично преобразуется в кинетическую энергию жидкости, вытекающей в атмосферу и частично превращается в тепло. Для схемы 2 имеем H=hпот, т.е. вся потенциальная энергия полностью преобразуется в тепло. Уравнения баланса энергии для обеих схем имеют одинаковый вид, а именно

В случае схемы 2 из всей суммы коэффициентов местных сопротивлений выделяется коэффициент внезапного расширения при входе трубы в емкость 2 (он равен единице, т.е. z = 1). Если труба круглая, то (2.6) преобразуется к виду (V = 4 Q/pd 2)
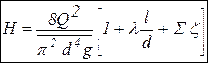
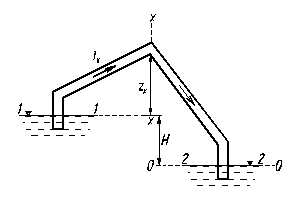
Это уравнение будем в дальнейшем называть уравнением для расчета простого трубопровода. Билет № 5 Билет № 6 Сифонный трубопровод Сифонным трубопроводом (сифоном) называется самотечный трубопровод, часть которого располагается выше уровня в сосуде (резервуаре), из которого происходит подача жидкости, рис. 10.1 Сифонные трубопроводы используют, например, в качестве водосбросов гидротехнических сооружений, для слива нефтепродуктов из цистерн, опорожнения водоемов через возвышенности, при самотечном соединении колодцев в системах водоснабжения и т. д. Для того, чтобы сифон начал работать, необходимо заполнить его жидкостью, удалив воздух. Этого можно достичь путем отсасывания воздуха в наивысшей точке сифона или заперев концы сифона, залить его жидкостью через верхнюю точку, где одновременно удаляют воздух. После сплошного заполнения сифона жидкостью он начинает работать как обыкновенная труба, поэтому расчет сифонного трубопровода принципиально ничем не отличается от расчета простого трубопровода. Если составить уравнение Бернулли для сечений 1 – 1 и 2 – 2 взяв за 0 – 0 плоскость отсчета и считать, что в резервуарах жидкость покоится, то получим
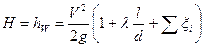
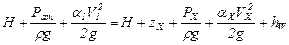 . .
Принимая V1=0 перепишем последнее уравнение в виде
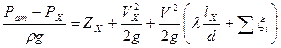 . .
Величина в левой части (10.3) представляет собой вакуум
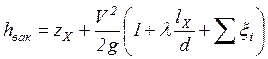 , ,
где V – средняя скорость жидкости в сифоне, zX – высота сечения с давлением pХ над уровнем жидкости в резервуаре 1, lX – длина части сифонной трубы от начала до сечения х – х. Из уравнения (10.4) следует, что hвак будет тем больше, чем больше zX, скорость V и потери напора; предельным местоположением сечения х – х будет наивысшее сечение трубы. Теоретически для нормальной работы сифонного трубопровода необходимо, чтобы минимальное давление в нем было всегда больше упругости паров жидкости при данной температуре
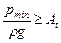 , ,
где pmin – минимальное давление в сифоне, ρ – плотность жидкости, At – упругость паров жидкости в м. ст. жидкости.
Билет №7 1)Открытые потоки(ур-ие равномерного движения,число Фруда) Открытые каналы Безнапорное движение жидкости имеет место в открытых руслах и характерно тем, что на свободной поверхности жидкости давление равно атмосферному, например, реки, каналы, лотки и т.д. При равномерном движении гидравлические элементы потока – площадь сечения, глубина и т.д. не изменяются по его длине; следовательно, равномерное движение невозможно в естественных руслах. На рис. 6.1 показан профиль потока в условиях равномерного движения. Глубина вдоль течения постоянна, поэтому гидравлический уклон равен пьезометрическому, т.е. уклону свободной поверхности и оба они равны уклону дна канала io.
Тяжести. При этом потенциальная энергия переходит в кинетическую и кинетическая энергия за счет трения преобразуется в тепло. Из (6.1) также следует, что до тех пор, пока к потоку применимо уравнение Бернулли потери на участке не зависят от шероховатости, а зависят от уклона дна. В открытых руслах, как правило, наблюдается турбулентный режим движения.
где S – площадь сечения, i – геометрический уклон, R – гидравлический радиус, С – коэффициент Шези, зависящий от гидравлического радиуса R и от шероховатости русла. Для коэффициента Шези предложено несколько зависимостей, одна из наиболее простых – формула И.И. Агроскина С = 1/ n + 17,72 lgR, где n – коэффициент шероховатости определяется по таблицам.
Билет №8 Характеристика трубопровода В гидравлических расчетах простых и сложных трубопроводов используют графические методы, которые во многих случаях облегчают решение задач. Эти методы основаны на графическом построении характеристик трубопроводов. Параллельное соединение При параллельном соединении участков трубопровода жидкость, подходя с расходом Q к точке их разветвления А, распределяется по ответвлениям и далее снова собирается в точке их соединения В, рис. 4.2. При параллельном соединение обычно заданы o Суммарный расход до точки разветвления, o Длина, диаметр, величина кэ каждой ветви. Основными задачами гидравлического расчета в этом случае являются. o Определение расходов Q1, Q2, Q3, …, Qn, на отдельных участках, соединенным параллельно. o Определение потерь напора Δh между точками А и В, на каждом участке. При решении задачи прежде всего учтём очевидное условие: равенство расхода Q сумме всех расходов на отдельных участках
Δh = Δh 1 = Δh 2 = Δh 3 = …= Δh n Решая систему уравнений (4.5), можно выразить все расходы через один (например, через Q1) и подставив затем эти значения расходов в (4.4) найти Q1. после этого с помощью (4.5) определяют последовательно расходы Q2, Q3, …, Qn, а по любому из уравнений системы (4.5) определяют потери напора Н. Билет №9 Билет №10 Билет №11 Схемы турбулентных потоков.
Вязкий слой расположен в непосредственной близости от стенки; в нём наблюдаются редкие турбулентные пульсации, но и они подавляются силами вязкости. Поэтому в весьма тонком вязком слое характер течения обуславливается в основном вязким трением. Средняя толщина вязкого слоя в такой схеме может быть больше или меньше средней высоты бугорков (выступов шероховатости стенок. На твердых и неподвижных стенках скорость равна нулю, а с удалением от них резко возрастает. В связи с этим получаются относительно большие градиенты скорости Толщина
где N-постоянная величина. В переходной области силы вязкого трения соизмеримы с движущими силами. Эта область располагается между вязким слоем и областью развитого турбулентного течения, называемой ядром турбулентного потока. Билет №12 Билет №13 1) хар-ка трубопровода!расчёт параллельного трубопровода Характеристика трубопровода В гидравлических расчетах простых и сложных трубопроводов используют графические методы, которые во многих случаях облегчают решение задач. Эти методы основаны на графическом построении характеристик трубопроводов. Параллельное соединение При параллельном соединении участков трубопровода жидкость, подходя с расходом Q к точке их разветвления А, распределяется по ответвлениям и далее снова собирается в точке их соединения В, рис. 4.2. При параллельном соединение обычно заданы o Суммарный расход до точки разветвления, o Длина, диаметр, величина кэ каждой ветви. Основными задачами гидравлического расчета в этом случае являются. o Определение расходов Q1, Q2, Q3, …, Qn, на отдельных участках, соединенным параллельно. o Определение потерь напора Δh между точками А и В, на каждом участке. При решении задачи прежде всего учтём очевидное условие: равенство расхода Q сумме всех расходов на отдельных участках
Δh = Δh 1 = Δh 2 = Δh 3 = …= Δh n Решая систему уравнений (4.5), можно выразить все расходы через один (например, через Q1) и подставив затем эти значения расходов в (4.4) найти Q1. после этого с помощью (4.5) определяют последовательно расходы Q2, Q3, …, Qn, а по любому из уравнений системы (4.5) определяют потери напора Н. Билет №14 1) Основное уравнение для расчёта простого трубопровода(вывод) Простой трубопровод – это труба постоянного диаметра с местными сопротивлениями, по которой проходит постоянный расход. Большинство простых трубопроводов вписывается в одну из следующих двух схем, рис. 2.1.; в резервуарах уровень поддерживается постоянным и поэтому течение везде установившееся.
Схема 1 Схема 2 Рис.2. 1. В обоих случаях движущей силой является сила тяжести, которая приводит к разности давлений и под действием этой разности жидкость приходит в движение. В обоих случаях потенциальная энергия положения преобразуется в кинетическую энергию, а последняя – в тепловую за счет сил трения.
Точнее результат для скорости течения получается, если приравнять запас потенциальной энергии и кинетическую энергию текущей жидкости. Для случая идеальной жидкости
В действительности вследствие вязкости (трение в жидкости) часть кинетической энергии переходит в тепловую. Поэтому чем больше сопротивлений по длине и местных, тем скорость течения меньше. Как это часто бывает, наиболее точный и исчерпывающий результат получается при решении общих уравнений. В данном случае вполне понятно, что основным уравнением, связывающим запас потенциальн
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.012 с.) |

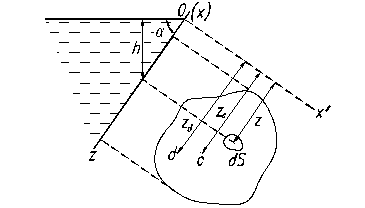 Определим силу F давления жидкости на площадку S, лежащую в плоскости стенки, расположенной под углом a к горизонту, рис. 8.1
Определим силу F давления жидкости на площадку S, лежащую в плоскости стенки, расположенной под углом a к горизонту, рис. 8.1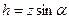 ,
,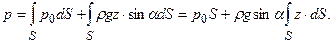

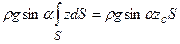
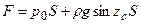
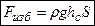
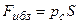
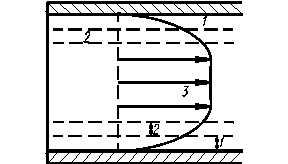 Рис.6.2
Рис.6.2
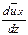 , что вызывает значительные касательные напряжения. Толщина вязкого слоя
, что вызывает значительные касательные напряжения. Толщина вязкого слоя 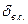 зависит от числа Рейнольдса, а именно толщина
зависит от числа Рейнольдса, а именно толщина 
 = 1,1 м/с; Re1 = 129511; Re1×
= 1,1 м/с; Re1 = 129511; Re1×  = 10,7; l1 = 0,017;
= 10,7; l1 = 0,017;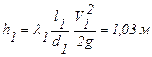
 = 31; l2 = 0,017;
= 31; l2 = 0,017; ; h1 + h 2 = 6.23 м.
; h1 + h 2 = 6.23 м.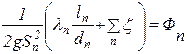
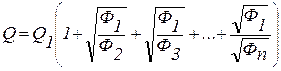
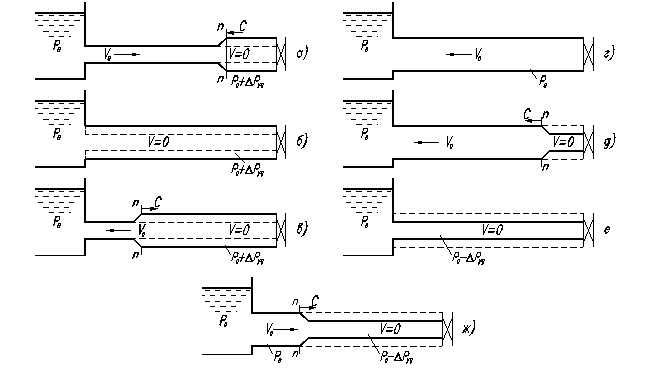 Рис.9.1
Рис.9.1
 Рис.9.2.
Рис.9.2.
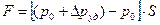 ,
,  , где S – площадь сечения трубы, ρ – плотность жидкости.
, где S – площадь сечения трубы, ρ – плотность жидкости.
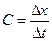

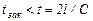 .
.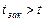 возникает не прямой гидравлический удар, при котором ударная волна, отразившись от резервуара, возвращается к крану раньше, чем он будет полностью закрыт. Повышение давления Δр при этом будет меньше, чем при прямом ударе, и оно может быть найдено по формуле
возникает не прямой гидравлический удар, при котором ударная волна, отразившись от резервуара, возвращается к крану раньше, чем он будет полностью закрыт. Повышение давления Δр при этом будет меньше, чем при прямом ударе, и оно может быть найдено по формуле  , где t – время закрытия запорного устройства. Резкое повышение давления при гидравлическом ударе представляет собой весьма опасное явление. Наиболее эффективным методом снижения Δр является устранение возможности прямого гидравлического удара, что при заданной длине трубопровода сводится к увеличению времени закрытия или открытия запорной или регулирующей аппаратуры. Гидравлический удар, рассматриваемый ранее, характеризующийся повышением давления, носит названии положительного удара.
, где t – время закрытия запорного устройства. Резкое повышение давления при гидравлическом ударе представляет собой весьма опасное явление. Наиболее эффективным методом снижения Δр является устранение возможности прямого гидравлического удара, что при заданной длине трубопровода сводится к увеличению времени закрытия или открытия запорной или регулирующей аппаратуры. Гидравлический удар, рассматриваемый ранее, характеризующийся повышением давления, носит названии положительного удара.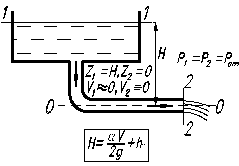
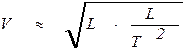 .
. или
или  .
. Уравнение (10.1) может быть решено относительно неизвестных H, Q и d, т. е. сифонный трубопровод может быть рассчитан в любой постановке задачи.
Уравнение (10.1) может быть решено относительно неизвестных H, Q и d, т. е. сифонный трубопровод может быть рассчитан в любой постановке задачи. Вместе с тем в расчете сифона есть и некоторая специфика. Очевидно, что жидкость движется по причине существования запаса потенциальной энергии за счет разности уровней Н; в то же время ясно, что при данной разности Н жидкость не может подняться неограниченно высоко в сифонной трубе. При расчетах необходимо дополнительно убедиться, не возникнет ли чрезмерный вакуум и не вызовет ли он вскипания жидкости, что нарушит работу сифона. Для этого составим уравнение Бернулли для сечений 1 – 1 и х – х, рис. 10.1. Относительно плоскости 0 - 0 получим
Вместе с тем в расчете сифона есть и некоторая специфика. Очевидно, что жидкость движется по причине существования запаса потенциальной энергии за счет разности уровней Н; в то же время ясно, что при данной разности Н жидкость не может подняться неограниченно высоко в сифонной трубе. При расчетах необходимо дополнительно убедиться, не возникнет ли чрезмерный вакуум и не вызовет ли он вскипания жидкости, что нарушит работу сифона. Для этого составим уравнение Бернулли для сечений 1 – 1 и х – х, рис. 10.1. Относительно плоскости 0 - 0 получим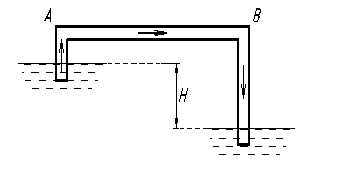 При расчетах рекомендуется назначить величину минимального давления значительно больше, во всяком случае для воды не менее 0,2 – 0,3 ат при нормальных температурных условиях. Этому значению соответствует наибольшая возможная высота расположения наивысшей точки сифона над свободной поверхностью жидкости в верхнем сосуде, равная примерно 7 м. Для того, чтобы избежать нарушения работы сифона надо либо уменьшить z, либо ввести дополнительные гидравлические сопротивления на нисходящем участке (ниже сечения х – х).
При расчетах рекомендуется назначить величину минимального давления значительно больше, во всяком случае для воды не менее 0,2 – 0,3 ат при нормальных температурных условиях. Этому значению соответствует наибольшая возможная высота расположения наивысшей точки сифона над свободной поверхностью жидкости в верхнем сосуде, равная примерно 7 м. Для того, чтобы избежать нарушения работы сифона надо либо уменьшить z, либо ввести дополнительные гидравлические сопротивления на нисходящем участке (ниже сечения х – х).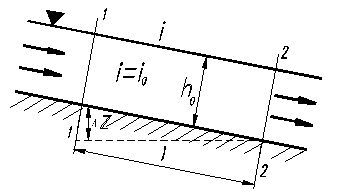 Рис.6.1
Рис.6.1