
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидравлический удар трубопровода(определение,фазы гидравлического удара,вывод ф-лы Жуковского)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гидравлическим ударом называется изменение давления в трубопроводе, вызванное резким изменением скорости движения жидкости во времени. Гидравлический удар может иметь место при быстром закрытии различных запорных устройств (задвижка, кран), внезапной остановки насосов, перекачивающих жидкость и т.д. Особенно опасен он в длинных трубопроводах, в которых движутся значительные массы жидкости с большими скоростями. В дальнейшем это повышение давления приводит к сжатию жидкости и расширению стенок трубы, т.е. производится работа. Фазы гидравлического удара Рассмотрим фазы гидравлического удара при закрытии трубы, по которой жидкость вытекает из открытого резервуара. Пусть в конце горизонтальной трубы, по которой жидкость движется со скоростью V0, произведено мгновенное закрытие крана, рис.9.1.а. При этом скорость частиц жидкости, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдёт в работу деформации стенок трубы и жидкости (стенки растягиваются, а жидкость сжимается). На заторможенные частицы у крана набегают другие, соседние с ними и тоже теряют скорость; в результате сечения n-n перемещается влево со скоростью с, называемой скоростью ударной волны. Сама же переходная область, в которой давление изменяется на величину Δpуд, называется ударной волной.
Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы растянутыми. Ударное повышение давления Δpуд распространится на всю трубу, рис.9.1.б. Но такое состояние не является равновесным. Под действием перепада давления Δpуд частицы жидкости устремятся из трубы в резервуар, причём это движение начнётся с сечения, непосредственно прилегающего к резервуару. Теперь сечение n-n перемещается в обратном направлении – к крану – с той же скоростью с, оставляя за собой выровненное давление р0, рис.9.1.в. Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию, соответствующие давлению р0. Работа деформации полностью переходит в кинетическую энергию и жидкость в трубе приобретает первоначальную скорость V0, но направленную теперь в противоположную сторону. С этой скоростью «жидкая колонна», рис.9.1.г, стремится оторваться от крана, в результате возникает отрицательная ударная волна (P0 - ΔPуд), которая направлена от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость, что обусловлено снижением давления, рис.9.1д. Кинетическая энергия жидкости вновь переходит в работу деформаций, но противоположного знака. Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рис.9.1.е. Так же как для случая, изображённого на рис.9.1.б, оно не является равновесным. На рис.9.1.ж показан процесс выравнивания давления в трубе и в резервуаре, сопровождающийся возникновением движения жидкости со скоростью V0. Очевидно, что как только отражённая от резервуара ударная волна под давлением Δpуд достигает крана, возникает ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторился. После нескольких циклов из-за возникающего при движении трения Δpуд постепенно уменьшается, и энергия рассеивания. Формула Н.Е. Жуковского для Δpуд Для определения Δpуд применим второй закон Ньютона в виде
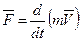 . .
 или или 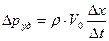 . Величина . Величина
Зависимость (9.4) носит название формулы Жуковского для величины превышения давления при гидравлическом ударе. Скорость распространения ударной волны с зависит от рода жидкости материала, диаметра, толщины стенок трубы и может быть найдена так
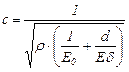
где ρ – плотность жидкости, Е0 – модуль упругости жидкости, d – внутренний диаметр трубы, Е – модуль упругости материала стенок трубы, δ – толщина стенок трубы. Для воды при обычных значениях отношения δ/d значения скорости с может приближённо приниматься равным 1200 м/с для стальных труб и 1000 м/с для чугунных. Формула (9.5) справедлива для так называемого прямого гидравлического удара. Гидравлическиё удар называется прямым, если время закрытия запорного устройства меньше времени двойного пробега ударной волны вдоль трубопровода При Гидравлический удар также может иметь место и при быстром открытии задвижки на напорном трубопроводе. В этом случае происходит значительное понижение давления в трубопроводе в результате резкого увеличения скорости. Такой гидравлический удар, характеризующийся понижением давления, носит название отрицательного удара. Билет №4 1)Основное уравнение для расчёта простого трубопровода(вывод) Простой трубопровод – это труба постоянного диаметра с местными сопротивлениями, по которой проходит постоянный расход. Большинство простых трубопроводов вписывается в одну из следующих двух схем, рис. 2.1.; в резервуарах уровень поддерживается постоянным и поэтому течение везде установившееся.
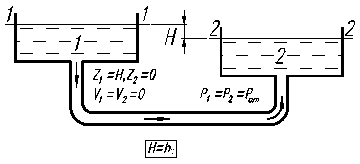
Схема 1 Схема 2 Рис.2. 1. В обоих случаях движущей силой является сила тяжести, которая приводит к разности давлений и под действием этой разности жидкость приходит в движение. В обоих случаях потенциальная энергия положения преобразуется в кинетическую энергию, а последняя – в тепловую за счет сил трения.
Точнее результат для скорости течения получается, если приравнять запас потенциальной энергии и кинетическую энергию текущей жидкости. Для случая идеальной жидкости
В действительности вследствие вязкости (трение в жидкости) часть кинетической энергии переходит в тепловую. Поэтому чем больше сопротивлений по длине и местных, тем скорость течения меньше. Как это часто бывает, наиболее точный и исчерпывающий результат получается при решении общих уравнений. В данном случае вполне понятно, что основным уравнением, связывающим запас потенциальной энергии, кинетическую энергию потока и потери является уравнение Бернулли
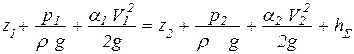
Суммарные потери hΣ складываются из потерь по длине hl и местных hм
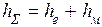 , ,
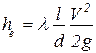
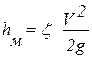 . .
Выбираем плоскость (ось) сравнения, совпадающей с осью горизонтальной части трубопровода, а сечения 1-1 и 2-2 совпадающими со свободными поверхностями в сосудах, рис. 2.1. Физический смысл уравнения для схемы 1 следующий: потенциальная энергия положения частично преобразуется в кинетическую энергию жидкости, вытекающей в атмосферу и частично превращается в тепло. Для схемы 2 имеем H=hпот, т.е. вся потенциальная энергия полностью преобразуется в тепло. Уравнения баланса энергии для обеих схем имеют одинаковый вид, а именно

В случае схемы 2 из всей суммы коэффициентов местных сопротивлений выделяется коэффициент внезапного расширения при входе трубы в емкость 2 (он равен единице, т.е. z = 1). Если труба круглая, то (2.6) преобразуется к виду (V = 4 Q/pd 2)
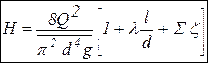
Это уравнение будем в дальнейшем называть уравнением для расчета простого трубопровода.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 624; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.012 с.) |

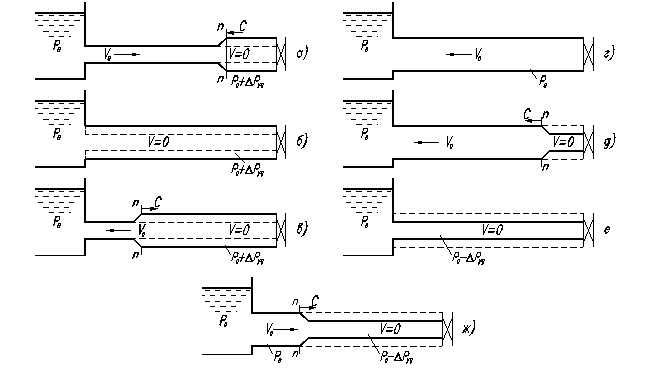 Рис.9.1
Рис.9.1
 Рис.9.2.
Рис.9.2.
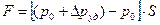 ,
,  , где S – площадь сечения трубы, ρ – плотность жидкости.
, где S – площадь сечения трубы, ρ – плотность жидкости.
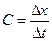

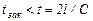 .
.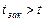 возникает не прямой гидравлический удар, при котором ударная волна, отразившись от резервуара, возвращается к крану раньше, чем он будет полностью закрыт. Повышение давления Δр при этом будет меньше, чем при прямом ударе, и оно может быть найдено по формуле
возникает не прямой гидравлический удар, при котором ударная волна, отразившись от резервуара, возвращается к крану раньше, чем он будет полностью закрыт. Повышение давления Δр при этом будет меньше, чем при прямом ударе, и оно может быть найдено по формуле  , где t – время закрытия запорного устройства. Резкое повышение давления при гидравлическом ударе представляет собой весьма опасное явление. Наиболее эффективным методом снижения Δр является устранение возможности прямого гидравлического удара, что при заданной длине трубопровода сводится к увеличению времени закрытия или открытия запорной или регулирующей аппаратуры. Гидравлический удар, рассматриваемый ранее, характеризующийся повышением давления, носит названии положительного удара.
, где t – время закрытия запорного устройства. Резкое повышение давления при гидравлическом ударе представляет собой весьма опасное явление. Наиболее эффективным методом снижения Δр является устранение возможности прямого гидравлического удара, что при заданной длине трубопровода сводится к увеличению времени закрытия или открытия запорной или регулирующей аппаратуры. Гидравлический удар, рассматриваемый ранее, характеризующийся повышением давления, носит названии положительного удара.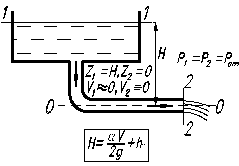
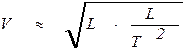 .
. или
или  .
.


