
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Давление покоющейся жидкости на плоской пов-ти. ВыводСодержание книги
Поиск на нашем сайте Одной из основных задач гидростатики является определение величины суммарной силы, действующей на плоскую поверхность со стороны покоящейся жидкости. Суммарная сила является вектором, и определение ее сведется к вычислению величины вектора, его направления и определению координат точки его приложения. Так как в каждой точке давление направлено по нормали к площадке, то и суммарная сила направлена по нормали.
F = р S где р – гидростатическое давление, S – величина площади. Решаемая ниже задача возникает по той простой причине, что в разных точках негоризонтальной стенки величина давления различная. Можно утверждать, что суммарная сила, действующая на любую площадку будет пропорциональна ее площади и будет иметь место формула вида (8.1); единственное, что необходимо при этом определить – в какой точке внутри площадки определяется давление р.
совмещения с плоскостью чертежа (т.е. на 90о). Тогда координатная ось Ох займет положение Ох1, ось Оz останется на месте, а площадка S изобразится на чертеже в натуральную величину. Представим площадку S состоящей из бесконечно малых частей dS. Рассмотрим одну из них, рис. 8.1. и допустим, что давление в ее центре равно р, тогда с точностью до бесконечно малых второго порядка можно записать для силы гидростатического давления, действующей на нее
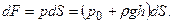
Всю силу F действующую на всю площадку S можно тогда записать в виде интеграла, т.е.
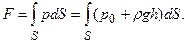
В последней формуле интеграл
равен статическому моменту площади S относительно координатной оси Ох1 (или Ох). Из теоретической механики известно, что статический момент некоторой площади S относительно заданной оси равен произведению площади S на расстояние от ее центра тяжести до оси. В данном случае
или, заменяя zc sina = hc, где hc – глубина погружения центра тяжести площади S под уровень свободной поверхности, получим выражение для силы полного (абсолютного) давления
 . .
или (так как rghc = рс)
где р с – гидростатическое давление в центре тяжести площадки. Таким образом, поставленная задача об определении величины силы решена. Билет №14 1) Основное уравнение для расчёта простого трубопровода(вывод) Простой трубопровод – это труба постоянного диаметра с местными сопротивлениями, по которой проходит постоянный расход. Большинство простых трубопроводов вписывается в одну из следующих двух схем, рис. 2.1.; в резервуарах уровень поддерживается постоянным и поэтому течение везде установившееся.
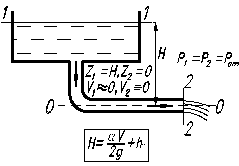
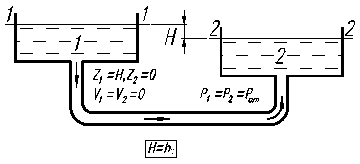
Схема 1 Схема 2 Рис.2. 1. В обоих случаях движущей силой является сила тяжести, которая приводит к разности давлений и под действием этой разности жидкость приходит в движение. В обоих случаях потенциальная энергия положения преобразуется в кинетическую энергию, а последняя – в тепловую за счет сил трения.
Точнее результат для скорости течения получается, если приравнять запас потенциальной энергии и кинетическую энергию текущей жидкости. Для случая идеальной жидкости
В действительности вследствие вязкости (трение в жидкости) часть кинетической энергии переходит в тепловую. Поэтому чем больше сопротивлений по длине и местных, тем скорость течения меньше. Как это часто бывает, наиболее точный и исчерпывающий результат получается при решении общих уравнений. В данном случае вполне понятно, что основным уравнением, связывающим запас потенциальной энергии, кинетическую энергию потока и потери является уравнение Бернулли
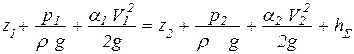
Суммарные потери hΣ складываются из потерь по длине hl и местных hм
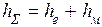 , ,
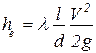
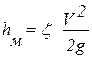 . .
Выбираем плоскость (ось) сравнения, совпадающей с осью горизонтальной части трубопровода, а сечения 1-1 и 2-2 совпадающими со свободными поверхностями в сосудах, рис. 2.1. Физический смысл уравнения для схемы 1 следующий: потенциальная энергия положения частично преобразуется в кинетическую энергию жидкости, вытекающей в атмосферу и частично превращается в тепло. Для схемы 2 имеем H=hпот, т.е. вся потенциальная энергия полностью преобразуется в тепло. Уравнения баланса энергии для обеих схем имеют одинаковый вид, а именно

В случае схемы 2 из всей суммы коэффициентов местных сопротивлений выделяется коэффициент внезапного расширения при входе трубы в емкость 2 (он равен единице, т.е. z = 1). Если труба круглая, то (2.6) преобразуется к виду (V = 4 Q/pd 2)
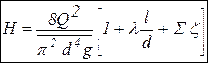
Это уравнение будем в дальнейшем называть уравнением для расчета простого трубопровода. 2) Открытые потоки(ур-ие равномерного движения,число Фруда)
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.006 с.) |

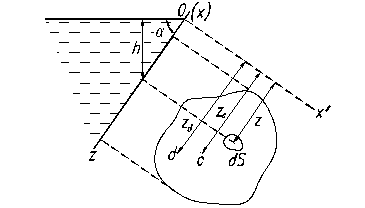 Определим силу F давления жидкости на площадку S, лежащую в плоскости стенки, расположенной под углом a к горизонту, рис. 8.1
Определим силу F давления жидкости на площадку S, лежащую в плоскости стенки, расположенной под углом a к горизонту, рис. 8.1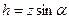 ,
,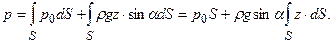

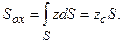
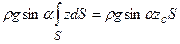
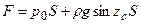
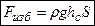
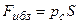
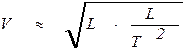 .
. или
или  .
.


