Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение скорости по сечению круглой трубы при турбулентном режиме.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для распределения скоростей в трубах часто используют эмпирические формулы, наиболее простой из которых является степенная
где um- значение скорости на расстоянии r от стенки (на оси трубы), u- скорость на расстоянии y от стенки трубы. Показатель степени n в этой формуле не постоянен и убывает с возрастание числа Re. Так, при Re =4.103 он равен 1/6, а при Re=32.105 – 1/10. Среднее значение n, соответствующее гладкостенному режиму, равно 1/7. Для этого случая зависимость (9.1) называется «закон одной седьмой» для распределения скорости
Отношение uср к umax в условиях ламинарного режима равно 0.5, а при турбулентном режиме как показывают опыты 0.85-0.95. Плавно изменяющееся движение и его основные особенности В действительности одномерных течений не существует, но некоторые реальные потоки с разной степенью достоверности могут быть сведены к одномерной модели. Например, при течении вязкой жидкости в круглой цилиндрической трубе имеет место неравномерное распределение скорости по сечению, но оно часто не принимается во внимание, так как во многих технических задачах достаточно знать среднюю по сечению скорость и закон изменения давления вдоль трубы. Заменив истинные, неравномерно распределенные по сечению скорости средней скоростью v и приняв давление р постоянным по сечению, переходим к одномерной модели реального потока. Переход от реальных течений к одномерной модели значительно упрощает задачу и позволяет получить простые зависимости, удобные для технических расчетов. Поток с изменяющимся по длине поперечным сечением будет трехмерным или пространственным, но в некоторых случаях приближенно может быть сведен к одномерной модели. Это возможно сделать, если: 1. линии тока представляют почти прямые линии (кривизна их очень мала); 2. угол между отдельными линиями тока очень мал, рис.6.1. Потоки, удовлетворяющие этим условиям, называют плавно изменяющимися. Билет № 3 1)Последовательное и параллельное соединение простых трубопроводов(исходные уравнение и методы решения) Рассмотрим систему из последовательно соединенных труб различных диаметров и длин. Такое соединение участков трубопровода называется последовательным, рис. 4.1.
Рис.4.1. Рис.4.2.
H = H1 + H2 + H3 + …+ Hn, где H1, H2 , H3, …, Hn – потери напора на 1, 2, 3, …n-ом участке. Учитывая, что для каждого участка последовательного соединения справедлива зависимость (2.7) и имея в виду, что на каждом участке расход одинаковый, запишем (4.2) в виде:
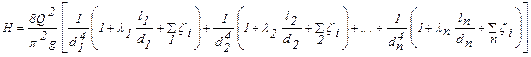 . .
Из (4.3) следует, что решение первой и второй задач при последовательном соединении участков трубопровода разного диаметра будет таким же как для простого трубопровода (трубопровода постоянного диаметра). Третья же задача, если в ней потребовать определения диаметров для всех участков, становится неопределенной, так как в этом случае уравнение (4.3) содержит n неизвестных. Для решения этой задачи необходимо задать диаметры труб для всех участков, кроме одного, который может быть тогда определен. Задача 4.1. Определить потери напора в стальном трубопроводе, состоящем из двух участков длиной l 1 = 120 м и l 2 = 250 м. Диаметры труб участков d 1 = 120 мм и d 2 = 100 мм. Расход воды в трубопроводе Q = 12,2 л/с, кинематический коэффициент вязкости воды принять равным n = 0,01 см2/с. Решение. В данном случае общие потери равны сумме потерь на каждом из участков. По справочнику определяем кЭ = 0,02 мм. Определяем последовательно для первого участка V1 =
Аналогично для второго участка V2 = 1,55 м/с; Re2 = 155414; Re2
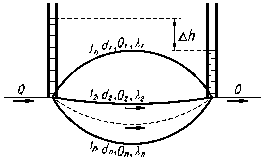
Ответ: общие потери напора равны 6,23 м. Параллельное соединение При параллельном соединении участков трубопровода жидкость, подходя с расходом Q к точке их разветвления А, распределяется по ответвлениям и далее снова собирается в точке их соединения В, рис. 4.2. При параллельном соединение обычно заданы o Суммарный расход до точки разветвления, o Длина, диаметр, величина кэ каждой ветви. Основными задачами гидравлического расчета в этом случае являются. o Определение расходов Q1, Q2, Q3, …, Qn, на отдельных участках, соединенным параллельно. o Определение потерь напора Δh между точками А и В, на каждом участке. При решении задачи прежде всего учтём очевидное условие: равенство расхода Q сумме всех расходов на отдельных участках
Δh = Δh 1 = Δh 2 = Δh 3 = …= Δh n Решая систему уравнений (4.5), можно выразить все расходы через один (например, через Q1) и подставив затем эти значения расходов в (4.4) найти Q1. после этого с помощью (4.5) определяют последовательно расходы Q2, Q3, …, Qn, а по любому из уравнений системы (4.5) определяют потери напора Н. Задача 4.2. Определить расходы и потери напора в каждой из n параллельно соединенных ветвей, считая, что как местные сопротивления, так и сопротивления по длине – в квадратичной области. Решение: В общем случае имеем для потерь в каждой ветви
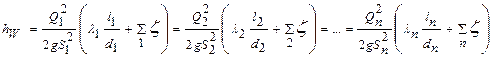
Имеем также
Примем обозначения
тогда уравнения (4.6) перейдут в такие
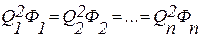
Из последнего уравнения выражаем все расходы через один, например через Q 1
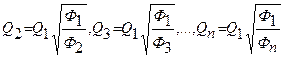
Затем из (4.7) получаем
Решая последнее уравнение относительно Q1, определим его значение, а из (4.9) и все остальные расходы; по любой из зависимостей (4.6) находим hW. Задача 4.3. Определить расходы и потери в каждой из трех ветвей параллельной сети, если длины и диаметры каждой из них равны соответственно l 1, l 2, l 3 и d 1, d 2, d 3. Известно, что местных сопротивлений нет, расход перед точкой разветвления равен Q, кинематический коэффициент вязкости n и то, что во всех трех ветвях движение ламинарное.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 602; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.007 с.) |

 (9.1)
(9.1) (9.2)
(9.2)
 = 1,1 м/с; Re1 = 129511; Re1×
= 1,1 м/с; Re1 = 129511; Re1×  = 10,7; l1 = 0,017;
= 10,7; l1 = 0,017;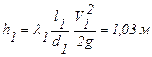
 = 31; l2 = 0,017;
= 31; l2 = 0,017; ; h1 + h 2 = 6.23 м.
; h1 + h 2 = 6.23 м.