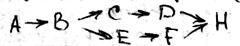Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Факторы, влияющие на скорость ферментативных р-цийСодержание книги
Поиск на нашем сайте
скорость многостадийного процесса, протекающего в полиферментной системе, зависит от концентрации промежуточных продуктов, а также от конц. соответствующего фермента и кофактора. Скорость каждой стадии определяется стационарной конц-ей данного промежуточного продукта, а также концентрацией соответствующего фермента. Стационарная конц. всех промежуточных продуктов, а также кофакторов определяется соотношением скоростей их образования и потребления и зависит не только от активности какой-то ферментативной системы, но и от скоростей других ферментативных р-ций, в к-рых эти соединения используются. На активность фермента в организма, а сл-но на скорость ферментативной р-ции влияет ряд факторов: сродство к субстрату, константа Михаэлеса, температура, рН среды, конц. с убстрата и разл. кофакторов, необходимых для действия ферментов, наличие активаторов и ингибиторов. Особую роль в регулировании активности ферментов играют коферменты. В случае отсутствие в организме достаточного количества коферментов и кофакторов активность ферментов снижается. Активность фермента зависит от конц. субстрата, участвующего в ферментативной р-ции. При стационарном состоянии р-ции субстрат поступает с такой же скоростью, с какой используется в р-ции. Повышение конц-ции субстрата вызывает ускорение р-ции до нового стационарного состояния, где новая скорость р-ции соответствует новой конц-ции субстрата. Известны полиферментные системы, в которых скорость ферментативных р-ций регулируется концентрацией конечного продукта в цепи последовательных превращений. В основе этого вида регуляции лежит ингибирование(или активация) ферментов 1-вой стадии биосинтеза конечными продуктами р-ции называемое ингибированием (или активацией) по типу обратной связи. Ингибиторы и активаторы, действующие по принципу обратной связи, называются эффекторами.
20 классификация ферментативных реакций по порядку. Хим р-ции, происх в био системах, делятся по молекулярности и по общему порядку. Мол-сть опред-ся числом частиц, которые участвуют в хим превращениях. Реакции в элементарных актах, которых участвуют 1, 2 или 3 частицы, называют моно-, би- и тримолекулярными р-циями. Вероятность столкновения более 3-х частиц мала и р-ции протекают в несколько элементарных стадий. Для био систем характерны моно- и бимол-ные р-ции. Важной хар-кой реакций явл скорость. Скорость хим процесса – это возрастание или уменьшение С вещества во времени. Число столкновений при заданных внешних условиях является ф-цией концентрации реагирующих в-в. Внешние условия – температура, давление, среда. В результате р-ции часть исходных молекул расходуется на образование продуктов р-ции и С исх в-в убывает, при этом скорость р-ции падает. Это является причиной того, что моно- и бимолекулярные р-ции идут с непрерывно убывающей скоростью. Если скорость р-ции не зависит от С реагентов, то её называют реакцией нулевого порядка. Пусть в-во А превращается в в-во В со скоростью, независимой от С вещества А. Примером могут быть ферментативные р-ции, идущие в условиях избытка субстрата. Кинетическое уравнение этого процесса имеет вид: da\ dt = -k0 db\dt = k0, в,а –концентрация в-в А и В. Решением этого уравнения являются линейные функции по времени: a= -k0t + C1 b= k0t + C2, где С – постоянная интегрирования -Коt, т.к. концентрация уменьшается Kot, т.к. концентрация растет Чтобы эти уравнения могли быть применимы на практике необходимо найти С при граничных условиях t=0, a=a0, b=0.
Кинетич. ур. им. вид: da\ dt = -k1а; db\dt = k1а;
Решением этого ур-ния явл. выраж: а=С1е-k 1 t или а= С1ехр(-k1t)
, при начал усл t=0, a=a0, b=0, С1=a0. С в-ва В получ из закона сохранения вещества а+b=a0, b=a0-a. Графическиски р-ция след образом:
Константа равновесия. Особенностью кинетики биологических процессов является наличие в системе агентов, способных влиять на скорость р-ций. К ним относятся ферменты, катализирующие биохим. превращения. Ферментативная кинетика изучает закономерности влияния химической природы реагирующих веществ и усл. их взаимодействия на скорость р-ций. На скорость хим. Р. влияют следующие факторы: -t0. v скорость р-ций увеличивается с увеличением температуры до определенного предела. -т.к.ферменты содержат Ко-ферменты и металлы, то скорость р.зависит от концентрации Ко-ферментов и металлов. -присутствия в р-ре разл. активизаторов и ингибиторов ферментов.
v1,v-1-v прям. И обр. р-ций. Чтобы выразить эту v: v1=k1[A]*[В], v-1=k-1[C]*[D] v1 пропорциональна произведению концентраций А и В, v-1 –концентраций С и D.к1 –константа скорости. это нормированная скорость, т.е. она равна скорости р-ции при концентрации реагирующих веществ =1. Если имеет место химическое равновесие, т.е. v1 = v-1 то можно записать: k1[A]*[В]= k-1[C]*[D] или k1\ k-1= [C]*[D]) \ ([A]*[В]) = keq, keq-константа равновесия -она равна произведению концентрации исх.в-в при состоянии равновесия.
Уравнение Михаэлеса-Ментен. В начале 20 в.было установлено, что если концентрацию F поддерживать, t- const, а начальную концентрацию субстрата изменять в широких пределах, то изменение начальной скорости р-ции выражается прямой с насыщением:
k2 k1
k1 1 2 на первой обратимой стадии образуется фермент-субстратный комплекс, который затем необратимо распадается на конечный продукт и освобождает молекулу F для участия в следующем цикле. Кинетическое изменение концентрации реагирующих веществ имеют вид: ds\dt= -k2 es + k -1 (es) de\dt = -k2 es + k -1 (es) +k1(es) d(es)\dt = k2es – k -1 (es) – k1(es) dp\dt = k1(es) = - ds\dt чтобы решить эту систему уравнений, наложим дополнительное условие закрытости на систему.Общее количество s, p в реакции остается сопst. Общ количество молекул F также постоянно. s+p = const e + (es) = e0 =const d(e+es))\dt=0 de\dt= -de\dt используя эти данные запишем с-му уравнений так: des\dt=k2s[e0 – (es)]-k-1(es-k1(es) des\dt=k2e0s – es (k2s + k-1 +k1)
(es)= k2e0s\ (k2s + k-1 +k1) или (es)= e0s\km+s –уравнение Михаэлис-Ментена
К m=к-1 +к1\к2 + s, Кm –константа Михаэлеса. По размерности и физ.смыслу Кm представляет собой концентрацию субстрата, при которой половина молекула субстрата, при котором половина молекул фермента пребывает в состоянии комплекса. Стационарность ферментативного процесса имеет место там,где конкуренция субстрата больше конкуренции фермента, т.е. происходит непрерывный приток субстрата и отток продуктов. Для скорости р-ции V=-ds\dt имеем V=k1е0\(кm+S) При очень большой концентрации S,Vстремиться VmaxS\(km+S) Лайнувер и Берк предложили перейти к линейной форме, где показывают обратную зависимость:1\v=1\vmax(km\S +1) – уравнение Лайнувер-Берка. Это у-ние наиболее удобно для проверки:
Константа равновесия. Особенностью кинетики биологических процессов является наличие в системе агентов, способных влиять на скорость р-ций. К ним относятся ферменты, катализирующие биохим. превращения. Ферментативная кинетика изучает закономерности влияния химической природы реагирующих веществ и усл. их взаимодействия на скорость р-ций. На скорость хим. Р. влияют следующие факторы: -t0. v скорость р-ций увеличивается с увеличением температуры до определенного предела. -т.к.ферменты содержат Ко-ферменты и металлы, то скорость р.зависит от концентрации Ко-ферментов и металлов. -присутствия в р-ре разл. активизаторов и ингибиторов ферментов.
v1,v-1-v прям. И обр. р-ций. Чтобы выразить эту v: v1=k1[A]*[В], v-1=k-1[C]*[D] v1 пропорциональна произведению концентраций А и В, v-1 –концентраций С и D.к1 –константа скорости. это нормированная скорость, т.е. она равна скорости р-ции при концентрации реагирующих веществ =1. Если имеет место химическое равновесие, т.е. v1 = v-1 то можно записать: k1[A]*[В]= k-1[C]*[D] или k1\ k-1= [C]*[D]) \ ([A]*[В]) = keq, keq-константа равновесия -она равна произведению концентрации исх.в-в при состоянии равновесия.
25 стационарное состояние и классификация полиферментных систем. Весь цикл обмена представляет собой открытую систему, в кот. Всё время поступают в-ва из внешней среды. Они претерпевают превращения в организме и удаляются в виде конечных продуктов. Регуляция биохимических процессов в клетке осуществляется с помощью прямой и обратной связи. Назначение регуляции состоит в том, чтобы поддерживать концентрации азличных в-в в клетке на уровне, кот. Определяется потребностями клетки. Большинство биохимических реакций катализируется ферментами, поэтому механизм регуляции заключается в изменении активности и концентрации фермента. Полиферментной называется система, взаимосвязанных ферментов, катализирующих различные стадии метаболических процессов. Если в полиферментной с-ме концентрации всех компонентов, а именно фермента, субстрата и продуктов р-ции, с течением времени остаются const, то с-ма нах-ся в стационарном состоянии. Отличие стационарной состояния от равновесного, что в стац состоянии ч\з с-му проходит постоянный стационарный поток в-ва и такое состояние х-ся const потоком энергии. По своему составу полиферментные системы могут быть гомои гетерогенными. Наиболее важными процессом в полиферментных с-мах можно классифицировать на следующие типы:
Разветвленные цепи; Полилинейные Цепи.
Распределительные системы Циклические системы;
Отдельно можем выделить саморегулирующая с-ма (с-мы с обратной связью)
26 свободно радикальные процессы в биологических системах в биологических процессах все виды пластического синтеза иэ энергообмена осуществляется дискретным путем, в котором большую роль играет одноэлектронная передача энергии и образование парамагнитных частиц с одиночными или неспаренными эл-ми(свободные радикалы). Свободные радикалы обладают высокой активностью. Меж числом неспаренных эл-нов и понятием свободная валентность атома есть прямое тождество. В-ва с неспаренными э-ми разделены на 2 гр: - в - ва,у которых неспаренные электроны связаны либо со всей мол екулой, либо с её большей частью. Эти неспаренные э-ны перемещаются по сильно делокализованным молекулярным орбиталям и обуславливают высокую активность внешних групп атомов. - в-ва, у которых неспаренные эл-ны связываются с молекулой с одним атомом. Они не перемещаются по молекулярным орбиталям, которые охватывали все атомы. Такие неспаренные Эл-ны связ. с атомами переходной группы(Fe,Co,Ni)/ эти неспаренные электроны представляют собой интерес для исследования полупроводниковых механизмов.
Именно этим определяется -монорадикалы с одним неспаренным Эл-ном(ОН-) -бирадикалы с 2-мя неспаренными Эл-ми. -ионрадикалы
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 606; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.21.101 (0.007 с.) |


 Реакция первого порядка – это процесс, скорость которого зависит от одной из концентраций (от С одного из веществ). Пусть вещество А превращается в вещество В со скоростью К1.
Реакция первого порядка – это процесс, скорость которого зависит от одной из концентраций (от С одного из веществ). Пусть вещество А превращается в вещество В со скоростью К1.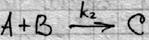
 Р-ция 2го порядка – это процесс, скорость которого зависит от концентрации реагир в-в. Пусть в-ва А и В дают в-во С со скоростью К2. Через х обозначим кол-во кажд в-ва, израсход на время t. Для кажд из этих в-в х будет один и тот же (т.к. в-ва взаимод в соотнош 1:1).Кин ур им вид: dx\dt = k2(a0 – x)(b0 – x) При изб 1го из реагентов р-ция 2го п-ка будет протек по схеме р-ции 1го порядка,т.к. С,напр, в-ва В будет изм-ся.
Р-ция 2го порядка – это процесс, скорость которого зависит от концентрации реагир в-в. Пусть в-ва А и В дают в-во С со скоростью К2. Через х обозначим кол-во кажд в-ва, израсход на время t. Для кажд из этих в-в х будет один и тот же (т.к. в-ва взаимод в соотнош 1:1).Кин ур им вид: dx\dt = k2(a0 – x)(b0 – x) При изб 1го из реагентов р-ция 2го п-ка будет протек по схеме р-ции 1го порядка,т.к. С,напр, в-ва В будет изм-ся.
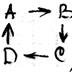
 Скорость р-ций подчиняется закону, согласно которому реакция идет быстрее, чем больше конц. в-в. Пусть мы имеем р-цию А+В С+D
Скорость р-ций подчиняется закону, согласно которому реакция идет быстрее, чем больше конц. в-в. Пусть мы имеем р-цию А+В С+D Эта кривая показывает, что зависимость вначале близка к линейной(при малых концентрациях субстрата), а затем достигает максимального значения. р-ции первого порядка при малых концентрациях субстрата переходят в р-ции нулевого порядка(т.е.при которых скорость р-ции не зависит от конц. Реагир-х в-в), скорость р-ции остается пропорциональной концентрации фермента.. Мат. модель F-ого катализа была разработана Михаэлесом и Ментеном в 1913г. они предложили двухстадийную последовательность процессов:
Эта кривая показывает, что зависимость вначале близка к линейной(при малых концентрациях субстрата), а затем достигает максимального значения. р-ции первого порядка при малых концентрациях субстрата переходят в р-ции нулевого порядка(т.е.при которых скорость р-ции не зависит от конц. Реагир-х в-в), скорость р-ции остается пропорциональной концентрации фермента.. Мат. модель F-ого катализа была разработана Михаэлесом и Ментеном в 1913г. они предложили двухстадийную последовательность процессов: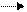

 E+S
E+S 
 ES E + P, где Р-продукт, S-субстрат, Е- фермент.
ES E + P, где Р-продукт, S-субстрат, Е- фермент.
 это означает, что кинетическая кривая компл.(es)будет содержать максимум. Производная в области макс. des\ dt=0 – условие стационарности процесса E +S Es E +P
это означает, что кинетическая кривая компл.(es)будет содержать максимум. Производная в области макс. des\ dt=0 – условие стационарности процесса E +S Es E +P решение уравнения при des\dt=0 дает нам:
решение уравнения при des\dt=0 дает нам: 23 уравнение Лайнувера-Берка
23 уравнение Лайнувера-Берка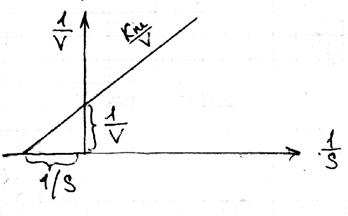

 Скорость р-ций подчиняется закону, согласно которому реакция идет быстрее, чем больше конц. в-в. Пусть мы имеем р-цию А+В С+D
Скорость р-ций подчиняется закону, согласно которому реакция идет быстрее, чем больше конц. в-в. Пусть мы имеем р-цию А+В С+D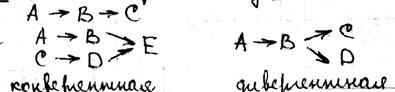 однолинейные цепи,
однолинейные цепи,