
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зависимости для коэфф гидравлического трения и области их примененияСодержание книги
Поиск на нашем сайте
Для определения потерь по длине применяется формула Дарси-Вейсбаха
Чтобы выбрать соответствующую зависимость для l предлагается простой алгоритм. Обычно заданы: расход Q, диаметр трубы d, кинематический коэффициент вязкости n и величина эквивалентной шероховатости kЭ (из таблиц) для данного материала. В таблице 8.1 приведены значения кэ для труб из разных материалов. Таблица 8.1
б) Число Рейнольдса Re=Vd/ν в) относительную шероховатость kЭ/d. 1. Если Re<2300, то имеет место ламинарный режим и 2. Если Re>4000, то определяют величину параметра 3. Если Re
4. Если 10< Re
5.Если Re
Билет №13 1) хар-ка трубопровода!расчёт параллельного трубопровода Характеристика трубопровода В гидравлических расчетах простых и сложных трубопроводов используют графические методы, которые во многих случаях облегчают решение задач. Эти методы основаны на графическом построении характеристик трубопроводов. Характеристикой трубопровода называется график зависимости суммарных потерь напора в трубопроводе от расхода. Для простого трубопровода потери равны требуемому напору, который в общем случае может быть найден по формуле
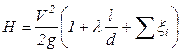 , ,
которая при заданных значениях l, d, ∑ζi, Кэ однозначно отражает зависимость напора Н от расхода Q.
hW = H = KQ2 , а если учитывать только сопротивления по длине, то (11.2) примет вид
Зависимости (11.1) и (11.2) возможно представить в координатах H – Q, задавая ряд значений Q и определяя соответствующие им значения Н.
Полученная на рис. 11.1 кривая представляет геометрический образ характеристики трубопровода. Если помимо гидравлических сопротивлений необходимо еще преодолеть геометрический напор Нг (высоту Нг или эквивалентную разность давлений), то график (характеристика трубопровода) будет иметь вид как на рис. 11.2 (Н = Нг при Q=0).
Заданы: общий расход и параметры каждой из ветвей. Необходимо найти потери напора и расход в каждой из них.
Параллельное соединение При параллельном соединении участков трубопровода жидкость, подходя с расходом Q к точке их разветвления А, распределяется по ответвлениям и далее снова собирается в точке их соединения В, рис. 4.2. При параллельном соединение обычно заданы o Суммарный расход до точки разветвления, o Длина, диаметр, величина кэ каждой ветви. Основными задачами гидравлического расчета в этом случае являются. o Определение расходов Q1, Q2, Q3, …, Qn, на отдельных участках, соединенным параллельно. o Определение потерь напора Δh между точками А и В, на каждом участке. При решении задачи прежде всего учтём очевидное условие: равенство расхода Q сумме всех расходов на отдельных участках
Δh = Δh 1 = Δh 2 = Δh 3 = …= Δh n Решая систему уравнений (4.5), можно выразить все расходы через один (например, через Q1) и подставив затем эти значения расходов в (4.4) найти Q1. после этого с помощью (4.5) определяют последовательно расходы Q2, Q3, …, Qn, а по любому из уравнений системы (4.5) определяют потери напора Н.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

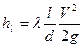
 1.Определяют
1.Определяют 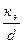

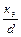 <500, то имеет место доквадратичная зона сопротивления l определяется по формуле Альтшуля.
<500, то имеет место доквадратичная зона сопротивления l определяется по формуле Альтшуля.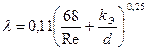
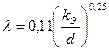
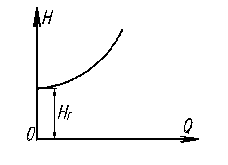



 Пример. Рассмотрим расчет параллельного соединения простых трубопроводов в общем случае, когда заранее неизвестны зоны сопротивления в ветвях. Допустим, что имеются три ветви (число их на ход расчета не влияет).
Пример. Рассмотрим расчет параллельного соединения простых трубопроводов в общем случае, когда заранее неизвестны зоны сопротивления в ветвях. Допустим, что имеются три ветви (число их на ход расчета не влияет).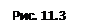 Для решения задачи строим на одном графике в координатах H – Q характеристики всех ветвей, рис. 11.3 (в общем случае все они будут разные). Затем строим результирующую характеристику по нескольким точкам. Для этого при некотором значении Н, одинаковом для всех характеристик суммируем расходы и получаем точку для построения результирующей характеристики. После того, как она построена по нескольким точкам, откладываем на оси Q заданный суммарный (общий) расход, находим искомое значение Н и по каждой из характеристик ветвей находим значения расходов Q1, Q2 и Q3.
Для решения задачи строим на одном графике в координатах H – Q характеристики всех ветвей, рис. 11.3 (в общем случае все они будут разные). Затем строим результирующую характеристику по нескольким точкам. Для этого при некотором значении Н, одинаковом для всех характеристик суммируем расходы и получаем точку для построения результирующей характеристики. После того, как она построена по нескольким точкам, откладываем на оси Q заданный суммарный (общий) расход, находим искомое значение Н и по каждой из характеристик ветвей находим значения расходов Q1, Q2 и Q3.


