
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Три задачи по расчёту внешнего трубопровода и их решение методом подбораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Все основные расчеты, связанные с простым трубопроводом сводятся к решению следующих трех задач. Задача 1. Заданы: Расход Q, диаметр d и длина l трубопровода, все величины местных сопротивлений zi, эквивалентная шероховатость материала стенок трубопровода кэ, кинематический коэффициент вязкости жидкости n. Определить: Напор H. Имея заданные величины, их подставляют в основную зависимость (2.7) и находят Н. Так что первая задача решается простым вычислением; она является основной, так как к ней сводится решение остальных двух. Типичный пример первой задачи – определение высоты водонапорной башни для создания заданного режима. Задача 3.1 Найти напор Н (например высоту Н водонапорной башни), если от нее по трубе диаметром d=50мм и длиной l=75м необходимо передать расход воды Q=3,5л/с. Трубы новые, стальные, КЭ=0,06мм, сумма всех коэффициентов местных сопротивлений равна 3,8, т.е. Σξ=3,8. Решение. Находим число Рейнольдса Re по формуле:
Затем находим значение параметра (Re·КЭ)/d=107 для установления зоны сопротивления. Зона сопротивления – доквадратичная, поэтому применяем формулу А. Д. Альтшуля
Таким образом искомое значение напора равно 6,4метра. Задача 2. Заданы: Напор H, диаметр d и длина l трубопровода, все величины zi, кэ и n. Определить: Расход Q. Ошибочной в данном случае может показаться простота решения уравнения (2.7) путем извлечения квадратного корня. На самом деле во всех зонах, кроме квадратичной, величина l зависит от числа Rе
а, следовательно, от расхода Q. Если подойти формально к решению второй задачи, то (2.7) представляет уравнение с одним неизвестным, которое решается по известным алгоритмам с помощью ЭВМ. В инженерной практике может быть полезен прием решения (2.7) называемый графоаналитическим способом. Если задаться несколькими (5 - 10) произвольными, но реальными числовыми значениями расхода Q и подставить их в (2.7), то получится столько же числовых значений Н. Затем в системе координат Q – H наносят эти точки и соединяют их плавной кривой; она, как видно из (2.7) представляет квадратичную параболу, симметричную относительно оси H, рис. 3.1., (имеет смысл ее ветвь при Q > 0). Построенная по точкам, она отражает зависимость Q от H только для данного трубопровода, поэтому из графика по известному значению Н находят искомое значение Q.
Рис. 3.1. Рис. 3.2. Необходимо задавать такие величины расходов, чтобы получать напоры как меньшие, так и большие заданного. Задача 3.2 Определить величину расхода Q, проходящему по трубопроводу диаметром d=50мм и длиной l=115м, если разность уровней в начале и в конце трубопровода равна Н=4,3м. Трубы стальные, КЭ=0,05мм, сумма всех коэффициентов местных сопротивлений равна 3,2, т.е. Σξ=3,2. Решение. В данном случае имеем одно уравнение (2,7) и одну неизвестную величину – расход Q, поэтому задачу лучше всего решать на ЭВМ одним из известных приближенных методов. Для инженерных расчетов применим простейший метод подбора. В качестве первоначального задаем расход, равный Q1=2,5л/с. Посмотрим теперь, какому значению напора Н соответствует заданное значение Q1=2,5л/с, т. е. решаем первую задачу по расчету простого трубопровода. Находим последовательно: Re1=63694, (Re1·КЭ)/d=64, λ1=0,023, Н1=4,8м. Получен напор, больший заданного, поэтому необходимо взять меньший расход, например Q2=2,2л/с, при этом расходе: Re2=56051, (Re2·КЭ)/d=56, λ2=0,024, Н2=3,8м. Ясно, что искомый расход заключен между Q1 и Q2 и любой расход, взятый из этого промежутка сужает интервал поиска. Продолжая задание расходов из интервала Q1 > QX > Q2 и сравнивая полученные значения НХ с заданным Н=4,3м, возможно решить задачу с любой точностью. Если в данном случае применить формулу
то получим (определяя λ как в квадратичной зоне) Q=2,57л/с, что является завышенным по сравнению с действительным значением. Задача 3. Заданы: Напор Н, расход Q, длина трубопровода, все величины zi, кэ и n. Определить: Диаметр d. В этом случае уравнение (2.7) невозможно решить аналитически, но формально – это уравнение с одним неизвестным и решение его на ЭВМ трудностей не представляет. Для инженерных расчетов удобно применить графо-аналитический способ. Кривая зависимости H от d является гиперболой; как это следует из (2.7): при d → 0, H → ∞. При d → ∞, H → 0, рис. 3.2. Для решения задач задают несколько значений диаметров, строят кривую и по известному значению Н находят искомое значение d. Задача 3.3. Определить диаметр трубопровода, который должен пропускать расход Q=5,6л/с при действуюшем напоре Н=3,0м. Длина трубопровода l=80м, КЭ=0,05мм, сумма коэффициентов местных сопротивлений на трубопроводе Σξ=4,5. Задача 3.4. При каких условиях решение задачи 2 (определение расхода) может быть получено в виде
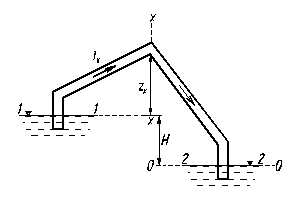
т.е. аналитически. Решение. Выражение, приведенное в условии задачи может быть получено в квадратичной области сопротивления, т.е. когда коэффициент гидравлического сопротивления l не зависит от числа Рейнольдса, а следовательно и от расхода. В этом случае точной является часто используемая при решении задач зависимость Н = K × Q 2, где К – постоянная, на зависящая от Q. Задача 3.5. Представим, что на дачном участке находится емкость с водой для полива, из которой выходит через отверстие отрезок шланга. Пояснить будет ли изменяться расход, а если будет, то как и по каким причинам, если: а) увеличить длину шланга; б) уменьшить диаметр шланга; в) немного прикрыть кран, ранее полностью открытый; г) изогнуть шланг (устроить поворот); д) увеличить диаметр шланга. Билет № 6 Сифонный трубопровод Сифонным трубопроводом (сифоном) называется самотечный трубопровод, часть которого располагается выше уровня в сосуде (резервуаре), из которого происходит подача жидкости, рис. 10.1 Сифонные трубопроводы используют, например, в качестве водосбросов гидротехнических сооружений, для слива нефтепродуктов из цистерн, опорожнения водоемов через возвышенности, при самотечном соединении колодцев в системах водоснабжения и т. д. Для того, чтобы сифон начал работать, необходимо заполнить его жидкостью, удалив воздух. Этого можно достичь путем отсасывания воздуха в наивысшей точке сифона или заперев концы сифона, залить его жидкостью через верхнюю точку, где одновременно удаляют воздух. После сплошного заполнения сифона жидкостью он начинает работать как обыкновенная труба, поэтому расчет сифонного трубопровода принципиально ничем не отличается от расчета простого трубопровода. Если составить уравнение Бернулли для сечений 1 – 1 и 2 – 2 взяв за 0 – 0 плоскость отсчета и считать, что в резервуарах жидкость покоится, то получим
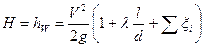
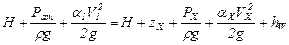 . .
Принимая V1=0 перепишем последнее уравнение в виде
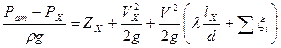 . .
Величина в левой части (10.3) представляет собой вакуум
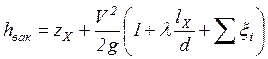 , ,
где V – средняя скорость жидкости в сифоне, zX – высота сечения с давлением pХ над уровнем жидкости в резервуаре 1, lX – длина части сифонной трубы от начала до сечения х – х. Из уравнения (10.4) следует, что hвак будет тем больше, чем больше zX, скорость V и потери напора; предельным местоположением сечения х – х будет наивысшее сечение трубы. Теоретически для нормальной работы сифонного трубопровода необходимо, чтобы минимальное давление в нем было всегда больше упругости паров жидкости при данной температуре
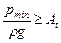 , ,
где pmin – минимальное давление в сифоне, ρ – плотность жидкости, At – упругость паров жидкости в м. ст. жидкости.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1278; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.012 с.) |

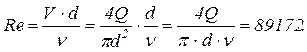
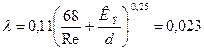 . Окончательно подставляем данные в формулу
. Окончательно подставляем данные в формулу
 ,
,
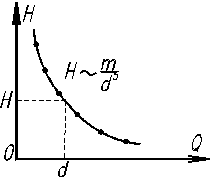
 ,
,
 Уравнение (10.1) может быть решено относительно неизвестных H, Q и d, т. е. сифонный трубопровод может быть рассчитан в любой постановке задачи.
Уравнение (10.1) может быть решено относительно неизвестных H, Q и d, т. е. сифонный трубопровод может быть рассчитан в любой постановке задачи. Вместе с тем в расчете сифона есть и некоторая специфика. Очевидно, что жидкость движется по причине существования запаса потенциальной энергии за счет разности уровней Н; в то же время ясно, что при данной разности Н жидкость не может подняться неограниченно высоко в сифонной трубе. При расчетах необходимо дополнительно убедиться, не возникнет ли чрезмерный вакуум и не вызовет ли он вскипания жидкости, что нарушит работу сифона. Для этого составим уравнение Бернулли для сечений 1 – 1 и х – х, рис. 10.1. Относительно плоскости 0 - 0 получим
Вместе с тем в расчете сифона есть и некоторая специфика. Очевидно, что жидкость движется по причине существования запаса потенциальной энергии за счет разности уровней Н; в то же время ясно, что при данной разности Н жидкость не может подняться неограниченно высоко в сифонной трубе. При расчетах необходимо дополнительно убедиться, не возникнет ли чрезмерный вакуум и не вызовет ли он вскипания жидкости, что нарушит работу сифона. Для этого составим уравнение Бернулли для сечений 1 – 1 и х – х, рис. 10.1. Относительно плоскости 0 - 0 получим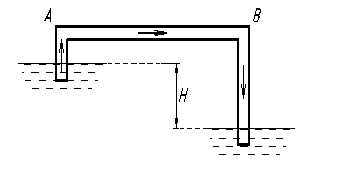 При расчетах рекомендуется назначить величину минимального давления значительно больше, во всяком случае для воды не менее 0,2 – 0,3 ат при нормальных температурных условиях. Этому значению соответствует наибольшая возможная высота расположения наивысшей точки сифона над свободной поверхностью жидкости в верхнем сосуде, равная примерно 7 м. Для того, чтобы избежать нарушения работы сифона надо либо уменьшить z, либо ввести дополнительные гидравлические сопротивления на нисходящем участке (ниже сечения х – х).
При расчетах рекомендуется назначить величину минимального давления значительно больше, во всяком случае для воды не менее 0,2 – 0,3 ат при нормальных температурных условиях. Этому значению соответствует наибольшая возможная высота расположения наивысшей точки сифона над свободной поверхностью жидкости в верхнем сосуде, равная примерно 7 м. Для того, чтобы избежать нарушения работы сифона надо либо уменьшить z, либо ввести дополнительные гидравлические сопротивления на нисходящем участке (ниже сечения х – х).


