
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введение. Предмет и задачи курса. Краткая история развития науки о гидравлике и пневматике.Содержание книги
Поиск на нашем сайте
ГИДРОСТАТИКА. Гидростатическое давление и его свойства Гидравлика делится на два раздела: гидростатика и гидродинамика. Гидродинамика является более обширным разделом и будет рассмотрена в последующих лекциях. В этой лекции будет рассмотрена гидростатика. Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение. Гидростатическое давление В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна. Рассмотрим резервуар с плоскими вертикальными стенками, наполненный жидкостью (рис.2.1, а). На дно резервуара действует сила P равная весу налитой жидкости G = γ V, т.е. P = G. Если эту силу P разделить на площадь дна Sabcd, то мы получим среднее гидростатическое давление, действующее на дно резервуара. Гидростатическое давление обладает свойствами: Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости. Для доказательства этого утверждения вернемся к рис.2.1, а. Выделим на боковой стенке резервуара площадку Sбок (заштриховано). Гидростатическое давление действует на эту площадку в виде распределенной силы, которую можно заменить одной равнодействующей, которую обозначим P. Предположим, что равнодействующая гидростатического давления P, действующая на эту площадку, приложена в точке А и направлена к ней под углом φ (на рис. 2.1 обозначена штриховым отрезком со стрелкой). Тогда сила реакции стенки R на жидкость будет иметь ту же самую величину, но противоположное направление (сплошной отрезок со стрелкой). Указанный вектор R можно разложить на два составляющих вектора: нормальный Rn (перпендикулярный к заштрихованной площадке) и касательный Rτ к стенке. Сила нормального давления Rn вызывает в жидкости напряжения сжатия. Этим напряжениям жидкость легко противостоит. Сила Rτ действующая на жидкость вдоль стенки, должна была бы вызвать в жидкости касательные напряжения вдоль стенки и частицы должны были бы перемещаться вниз. Но так как жидкость в резервуаре находится в состоянии покоя, то составляющая Rτ отсутствует. Отсюда можно сделать вывод первого свойства гидростатического давления. Свойство 2. Гидростатическое давление неизменно во всех направлениях. В жидкости, заполняющей какой-то резервуар, выделим элементарный кубик с очень малыми сторонами Δx, Δy, Δz (рис.2.1, б). На каждую из боковых поверхностей будет давить сила гидростатического давления, равная произведению соответствующего давления Px, Py, Pz на элементарные площади. Обозначим вектора давлений, действующие в положительном направлении (согласно указанным координатам) как P'x, P'y, P'z, а вектора давлений, действующие в обратном направлении соответственно P''x, P''y, P''z. Поскольку кубик находится в равновесии, то можно записать равенства P'xΔyΔz=P''xΔyΔz P'yΔxΔz = P''yΔxΔz P'zΔxΔy + γΔx, Δy, Δz = P''zΔxΔy где γ - удельный вес жидкости; Δx, Δy, Δz - объем кубика. Сократив полученные равенства, найдем, что P'x = P''x; P'y = P''y; P'z + γΔz = P''z Членом третьего уравнения γΔz, как бесконечно малым по сравнению с P'z и P''z, можно пренебречь и тогда окончательно P'x = P''x; P'y = P''y; P'z=P''z Вследствие того, что кубик не деформируется (не вытягивается вдоль одной из осей), надо полагать, что давления по различным осям одинаковы, т.е. P'x = P''x = P'y = P''y = P'z=P''z Это доказывает второй свойство гидростатического давления. Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве. Это положение не требует специального доказательства, так как ясно, что по мере увеличения погружения точки давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться. Третье свойство гидростатического давления может быть записано в виде P=f(x, y, z) Основное уравнение гидростатики P = P0 + ρgh – основное уравнение гидростатики. Данное выражение является математическим выражением закона распределения полного абсолютного гидростатического давления в некоторой точке, погружённой на глубину h относительно свободной поверхности, равна сумме внешнего давления P0 на свободную поверхность и давление веса столба жидкости ρgh. Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее всегда будет действовать давление, приложенное к внешней поверхности P0. Другими словами давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково.
ЭЙЛЕРА УРАВНЕНИЕ В гидромеханике-дифференц. ур-ние движения идеальной жидкости в переменных Эйлера. Если давление р, плотность р, проекции скоростей частиц жидкости и, v, w к проекции действующей объёмной силы X, Y,Z рассматривать как ф-ции координат х, у,z точек пространства и времени t (переменные Эйлера), то Э. у. в проекциях на оси прямоуг. декартовой системы координат принимает вид системы ур-ний:
Решение общей задачи гидромеханики в переменных Эйлера сводится к тому, чтобы, зная X, Y,Z, а также начальные и граничные условия, определить u,w,v,p как ф-ции х, у, z и t. Для этого к Э. у. присоединяют ур-ние неразрывности в переменных Эйлера:
В случае баротропной жидкости, у к-рой плотность зависит только от давления, 5-м ур-нием будет ур-ние состояния
Уравнение состояния газов Газы характеризуются значительной сжимаемостью и высоким коэффициентом теплового расширения. Сжатие газов – процесс механического воздействия на них, связанного с изменением объема V и температуры T. В этом случае давление газа определяется функциональной зависимостью: P=f(V,T) – уравнение состояния газа. Из термодинамики известно, что для равновесных систем состояние газа является определенным, если известны его основные параметры(объем или плотность, давление и температура). Если процесс протекает при постоянном значении какого либо параметра, то имеем простейший термодинамический процесс. Характерные процессы: 1. Изохорный – V=const P1/P2=T1/T2 - Уравнение Шарля 2. Изотермический – T=const P1/P2=V2/V1 - 3. Изобарный – P=const V1/V2=T1/T2 - Уравнение Гей – Люсака 4. Адиабатный – при отсутствии теплообмена между газом и окружающей средой P*V^k=const 5. Политропный – при частичном теплообмене между газом и окружающей средой P*V^n=const
k=Cp/Cv Cp – теплоемкость газа при P=const Cv – теплоемкость газа при V=const Существует обобщенный закон состояния газа (Уравнение Клапейрона – Менделеева): P*V=R*T*m/M= [ню]* R*T P/[ро]=R*T Расчёт заторможенного газа. Параметры газа в состоянии покоя при адиабатическом процессе сжатия без потерь энергии называется параметрами заторможенного газа. I=Cp*T; i(нулевое)=Cp*T(нулевое) Cp-теплоёмкость газа при постоянном давлении. T-температура газа. I(нулевое)-энтальпия заторможенного потока. т.е это значение I когда W=0. T(нулевое)-температура заторможенного потока. Cp+T+W в квадрате/2=Cp*T(нулевое) T=p/g(плотность)*R; T(нулевое)=p(нулевое)/g(плотность нулевая)*R R-газовая постоянная; R=Cp-Cv. Cv-теплоёмкость газа при постоянном объёме. Cp/Cp-Cv*p/g(плотность)+W в квадрате/2= Cp/Cp-Cv *p(нулевое)/g(плотность нулевая). Cp/Cv=K- показатель изоэнтрапии. В частном случаи для равновесного теплоизолирования системы показатель адиабата равен показателю политропа. K*Cv/K*Cv-Cv=K/K-1 Для адиабатического процесса давление и плотность газа связанно следующим соотношением: p/p(нулевое)=(g/g(плотность нулевая)) всё в степени K) Используя уравнение состояния газа можно получить отношение температур при адиабатическом отношении: T/T(нулевое)=p/p(нулевое)*g(плотность)/g(нулевую плотность)=(g/g(нулевая)) в степени k-1 p/p(нулевое)=(T/T(нулевое)) в степени k/k-1.
Общий к.п.д. насоса КПД насоса есть отношение полезной мощности к мощности, потребляемой насосом
Подобно тому, как это принято для лопастных насосов, для объемных насосов различают гидравлический
где Умножим и разделим уравнение (2.7.8) на
т. е. КПД насоса (общий) равен произведению трех частных КПД — гидравлического, объемного и механического. КПД поршневых насосов зависит от размеров насоса и его конструкции, рода подаваемой жидкости и главным образом от развиваемого им давления. При давлении до 10 МПа η=0,9-0,92; при давлении 30-40 МПа η=0,8-0,85; при этом снижении КПД с увеличением давления зависит не только от конструкции насоса, но и от модуля упругости подаваемой жидкости, который снижается благодаря пузырькам газов.
Характеристика трубопровода Характеристикой трубопровода называется зависимость суммарной потери напора (или давления) в трубопроводе от расхода:
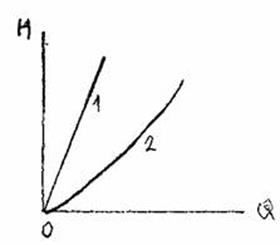
График уравнения простого трубопровода H=f(Q) носит название его гидравлической характеристики.
Вид гидравлической характеристики зависит от режима движения жидкости в трубопроводе: при ламинарном движении жидкости гидравлическая характеристика трубопровода - прямая линия, проходящая через начало координат (1). При турбулентном режиме гидравлическая характеристика - парабола (2).
Если на трубопроводе собранном из труб одинакового диаметра имеются местные сопротивления, то такой трубопровод можно привести к простому трубопроводу эквива длины:
Шестеренные насосы. Шестеренный насос является представителем роторных насосов вращательного типа. Роторный насос – это объемный насос, в котором вытеснение жидкости производится из перемещаемых рабочих камер в результате вращательного или вращательного и возвратно-поступательного движения рабочих органов – вытеснителей. В роторно-вращательных насосах вытеснители совершают только вращательное движение. Шестеренные насосы выполняются с шестернями внешнего и внутреннего зацепления. Наибольшее распространение имеют насосы с шестернями внешнего зацепления На рис. 15 приведена схема такого насоса. Он состоит из двух одинаковых шестерен - ведущей 2 и ведомой 3, помещенных в плотно охватывающем их корпусе - статоре 1. При вращении шестерен в направлении, указанном стрелками, жидкость, заполняющая впадины между зубьями, переносится из полости всасывания в полость нагнетания. Вследствие разности давлений (p2>p1) шестерни подвержены воздействию радиальных сил, которые могут привести к заклиниванию роторов. Для уравновешивания последних в корпусе насосов иногда устраивают разгрузочные каналы 4. Такие же каналы могут быть выполнены и в самих вторах.
2 1 Рис. 15. Шестеренный насос Рис. 16. Шестеренный насос с гидростатическим прижимом. В шестеренных насосах высокого давления (свыше 10 МПа) предусматривается гидравлическая компенсация торцевых зазоров, осуществляемая специальными 'плавающими втулками", которые давлением жидкости прижимаются к шестерням. Подвод давления нагнетания по каналу 4 и дренаж через каналы 3 в корпусе о позволяют обеспечить компенсацию торцевого зазора между шестернями 1 и боковыми щеками 2 и 5. Чаше всего применяются насосы, состоящие из пары прямозубых шестерен с внешним зацеплением и с одинаковым числом зубьев эвольвентного профиля. Для увеличения подачи иногда употребляются насосы с тремя и более шестернями, размещенными вокруг центральной ведущей шестерни. Для повышения давления жидкости применяются многоступенчатые шестеренные насосы. Подача каждой последующей ступени этих насосов меньше подачи предыдущей ступени. Для отвода излишка жидкости каждая ступень имеет перепускной (предохранительный) клапан, отрегулированный на соответствующее максимально допустимое давление. Кроме прямозубых шестерен, выполняются насосы с косозубыми и шевронными шестернями. Угол наклона зубьев в шевронных шестернях обычно составляет 20*—25*. Современные шестеренные насосы могут развивать давления до 10-20 МПа. Для приближенных расчетов минутной подачи насосов с двумя одинаковыми шестернями можно пользоваться формулой: где Для шестерен с нормальным эвольвентным некорригированым зацеплением A= При z < 16 в шестеренных насосах обычно применяется корригированное эвольвентное зацепление, при котором h = m1, a Насосы типов НШ и НМШ предназначены для нагнетания рабочей жидкости в гидравлические системы тракторов, подъемных землеройных, дорожно-строительных, транспортных и других сельскохозяйственных машин. В их числе насосы НШ 10-10-2, НШ32-10-2 и НШ32-32-2 двухсекционные; насосы НМШ 50 и НМШ125 - двухкамерные. Насосы типа (Ш предназначены для подачи масла, нефти, мазута, дизельного топлива; насосы ШГ-для подачи парафина, нефти, мазута с температурой не менее 100 °С и и до 6-104 м2/с; насосы ШФ предназначены для подачи масла, нефти, дизельного топлива с температурой до 90 °С. Насосы П1-2 и БП1-2 используются в системе станочных гидроприводов.
Введение. Предмет и задачи курса. Краткая история развития науки о гидравлике и пневматике. Гидравлика – прикладная наука, изучающая законы равновесия и движения жидкости и разрабатывающая на основе теории и эксперимента способы применения этих законов к решению различных задач инженерной практики. Слово «гидравлика» произошло от слияния двух греческих слов «хюдор» - вода и «аулос» - труба, канал, струя. Гидравлика – очень древняя наука. За несколько тысяч лет до нашей эры в Индии, Китае, в Египте, странах Ближнего и Среднего востока уже строились различные гидротехнические сооружения: каналы, платины, водяные колеса. Методов расчета этих сооружений в то время не существовало и определенные достижения в гидротехническом строительстве были возможны благодаря искусству и практическому опыту строителей. Первым научным трудом в области гидравлики считается написанный примерно за 250 лет до н.э. трактат Архимеда «О плавающих телах», в котором величайший ученый древности сформулировал закон о давлении жидкости на погруженное в нее тело. Особое развитие гидравлика получила в средние века. В XV веке Леонардо да Винчи написал труд «О движении и измерении воды в тесных сооружениях», опубликованный через 307 лет после его смерти в 1826 году. В 1586 году голландский ученый Симон Стевин опубликовал работу «Начало гидростатики». В XVI – XVII веках Г. Галилей, Э. Таричелли, Б. Паскаль и И. Ньютон проводили исследования, позволившие разработать основы гидромеханики. В 1755 – 1756 годах выходят в свет работы Л.П. Эйлера, где впервые приводится полная система дифференциальных уравнений равновесия и движения идеальной ж. Основоположниками гидравлики как самостоятельной науки являются члены Петербургской академии наук М.В. Ломоносова, Д.И. Бернулли, Л.П. Эйлер. В 1738 году была опубликована работа Д. Бернулли «Гидравлика или записки о силах движения жидкости», в которой установлена зависимость между давлением и скоростью в элементарной струйке идеальной жидкости. Представляют интерес такие работы Шизе, Вентури, Вейсбаха, Дарси, Базена и Рейнольдса. Труды этих ученых посвящены главным образом изучению турбулентности потоков и установлению общих законов сопротивления движению вязких жидкостей, а также исследованию движения жидкости в трубах, каналах и на водосливах. Большое внимание уделено в них также разработке теории размерности и подобия и постановке лабораторных экспериментов. В 1791 году вышла в свет первое русское руководство по гидравлике А. Колмакова «Карманная книжка для вычисления количества воды, вытекающей через трубы, отверстие или по желобам, также и силы, какой они ударяют, стремясь с данной скоростью». В конце XIX – начала XX века появились работы русских ученных: И.С. Громека, предположившего уравнения вихревого движения жидкости; Н.П. Петрова, разработавшего гидродинамическую теорию смазки; Н.Е. Жуковского, создавшего теорию гидравлического удара в трубах. Большой вклад в развитие гидравлики принесли советские ученые: А.Н.Колмогоров (теория турбулентности), Н.Н Павловский (теория фильтрации, равномерное и неравномерное движение жидкости), И.Н. Куколевский (теория машиностроительной гидравлики), С.А.Христианович (неустановившиеся движения жидкости) и многое другие. Гидравлику как прикладную инженерную науку широко используют в различных областях техники, она дает методы расчета и проектирования разнообразных гидротехнических сооружений, гидромашин и состоящих из них самых различных гидросистем, которые широко используются в машиностроении, на транспорте, в авиации и других отраслях промышленности. Для расчета и проектирования таких гидросистем гидромашин, гидроприводов и систем их автоматического регулирования, а также для правильной их эксплуатации, ремонта и наладки нужно иметь соответствующую подготовку в области гидравлики и теории гидромашин. Получить такую подготовку и является основной задачей стоящей перед нашим курсом.
3.Жидкости и их свойства. Жидкостью называется сплошная среда, образующая способностью легко изменять свою форму под действием даже незначительных сил. Жидкость – агрегатное состояние вещества, сочетающая в себе черты как твердого, так и газообразного состояния. Благодаря легкоподвижности частиц, обусловленной слабостью сил межмолекулярного сцепления, и, следовательно неспособностью воспринимать в состоянии покоя даже малые касательные напряжения, жидкости легко изменяют свою форму, принимая форму того сосуда, в котором они находятся. Эта способность жидкости неограниченна деформироваться под действием сколь угодно малых сил называются текучестью. Это одно из основных свойств жидкостей. 1. Плотность – ρ – называют массу жидкости в единице объема 2. Удельным весом – γ – называют вес жидкости в единице объема 3. Сжимаемость жидкости – это ее свойство изменять свой объем под действием давления, характеризующийся коэффициентом объемного сжатия βp, который представляет собой относительное изменение объема, приходящееся на единицу давления. 4. Упругость – свойство жидких тел восстанавливать свой объем после прекращения действия внешних сил. Упругость характеризуется модулем объемной упругости Eo, величина которого обратная коэффициенту объемного сжатия 5. Температурные расширения характеризуется коэффициентом температурного расширения 6. На поверхности раздела жидкости и газа действующие силы поверхностного помещения, стремящиеся придать объему жидкости сферическую форму и вызывающие некоторое дополнительное давление. Однако это давление заметно сказывается лишь при малых объемах жидкости и для сферических объемов (капель) В трубках малого диаметра поверхностное натяжение вызывает подъем (или опускания) жидкости относительно нормального уровня. Это явление называется капиллярным эффектом. 7. Вязкость – это свойство жидкости оказывать сопротивление относительному движению (сдвигу) слоев жидкости. Представим слой, движущейся жидкости вдоль поверхности. В случае тормозящего влияния стенки слои и жидкости будут двигаться… с разными скоростями, значения, которых возрастают по мере отдаления от стен. Рассмотрим два слоя жидкости, движущейся на расстоянии dy друг от друга. Вследствие разности скоростей один слой движется быстрее другого на величину du, а величине du/dy является градиентом скорости. Возникающее при этом относительном движении касательное напряжение В практических расчетах часто пользуются кинематическим коэффициентом вязкости, представляющим собой отношение динамического коэффициента вязкости к плотности жидкости. Кроме перечисленных, жидкости обладают целым рядом свойств, таких как газосодержание, испарение, кипение, теплоемкость и др.,
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 556; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.119.34 (0.015 с.) |



 (или когда жидкость несжимаема)
(или когда жидкость несжимаема)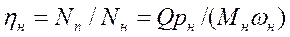 (2.8)
(2.8)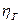 , объемный
, объемный 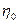 и механический
и механический 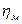 КПД, учитывающие три вида потерь энергии: гидравлические — потери напора (давления), объемные — потери на перетекание жидкости через зазоры, и механические — потери на трение в механизме насоса:
КПД, учитывающие три вида потерь энергии: гидравлические — потери напора (давления), объемные — потери на перетекание жидкости через зазоры, и механические — потери на трение в механизме насоса: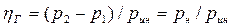 (2.9)
(2.9)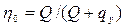 (2.10)
(2.10)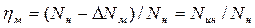 (2.11)
(2.11) — индикаторное давление, создаваемое в рабочей камере насоса и соответствующее теоретическому напору в лопастном насосе;
— индикаторное давление, создаваемое в рабочей камере насоса и соответствующее теоретическому напору в лопастном насосе; 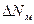 — потери мощности на трение в механизме насоса;
— потери мощности на трение в механизме насоса; 
 — индикаторная мощность, сообщаемая жидкости в рабочей камере и соответствующая гидравлической мощности в лопастных насосах.
— индикаторная мощность, сообщаемая жидкости в рабочей камере и соответствующая гидравлической мощности в лопастных насосах.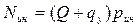 и произведем перегруппировку множителей. Получим
и произведем перегруппировку множителей. Получим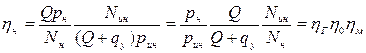 (2.12)
(2.12)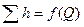
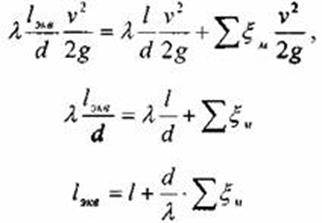



 - объемный КПД насоса, зависящий от конструкции, технологии изготовления и давления насоса и принимаемый равным 0,7 - 0,95; А - расстояние между центрами шестерен, равное при одинаковых шестернях диаметру начальной окружности D;
- объемный КПД насоса, зависящий от конструкции, технологии изготовления и давления насоса и принимаемый равным 0,7 - 0,95; А - расстояние между центрами шестерен, равное при одинаковых шестернях диаметру начальной окружности D;  где
где  - внутренний диаметр шестерни.
- внутренний диаметр шестерни. = mz, высота головки зуба h=m и
= mz, высота головки зуба h=m и  где m - модуль зацепления и z - число зубьев шестерни. Для таких шестерен формула принимает вид:
где m - модуль зацепления и z - число зубьев шестерни. Для таких шестерен формула принимает вид: 
 , а рабочий объем насоса
, а рабочий объем насоса  . Таким образом, рабочий объем шестеренного насоса пропорционален произведению диаметра D и модуля m. Поэтому для уменьшения габаритов насоса выгоднее при его проектировании выбирать большее значение mи меньшее число z, а следовательно, и D. Однако уменьшение z требует увеличения степени корригирования и увеличивает неравномерность подачи.
. Таким образом, рабочий объем шестеренного насоса пропорционален произведению диаметра D и модуля m. Поэтому для уменьшения габаритов насоса выгоднее при его проектировании выбирать большее значение mи меньшее число z, а следовательно, и D. Однако уменьшение z требует увеличения степени корригирования и увеличивает неравномерность подачи. т, который представляет собой относительное изменение объема жидкости при изменении температуры на 1˚С
т, который представляет собой относительное изменение объема жидкости при изменении температуры на 1˚С на границе слоев аналогично явлению сдвига в твердых телах и пропорционально градиенту скорости деформации,
на границе слоев аналогично явлению сдвига в твердых телах и пропорционально градиенту скорости деформации,


