
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенный метод решения задачи (4.1) – (4.2)Содержание книги
Поиск на нашем сайте
Отрезок Обозначим Мы знаем, что
При малых h справедливо соотношение
или
Аналогично получится приближенная формула
т.е. считаем, что площадь поперечного сечения Q постоянная величина вдоль трубопровода. На основе этих формул из (4.1) получается приближенное неравенство.
Предполагая, что h малая величина составляем равенства
i=1, 2, …, n-1.
где (4.3) – (4.4) является разностной задачей.
Теорема – 1. Если
где C- константа, зависящая от начальных данных. Из (4.5) становится ясно, что при малом h в качестве
4.4. Трехточечная разностная схема. Метод прогонки Из (4.3) – (4.4) получаем равенства
где
(4.6) – называется трехточечной разностной схемой. Это есть система n-1 линейных алгебраических уравнений c Система (4.6) решается методом прогонки. Предполагаем, что решение (4.6) имеет вид
Подставляем его в (4.6). Тогда,
или
Сравнивая (4.7) и (4.8) получим соотношения
Из (4.7) при l = n-1 получим
Из этого тождества получим
Из (4.9) и (4.10) определяются все
После этого из (4.7) используя
Теорема 2. Если В нашем случае оба неравенства выполняются, поэтому метод прогонки является устойчивым.
Переменные. Блок-схема
Из определения Аі, Ві, Сі следует равенства
Сі = Аі -1, Ві = Аі +Аі - 1 + а2 h2
Поэтому, (4.9) можно переписать в виде
На основе этих формул, при программировании используются массивы A[0…n], α[0…n-1], β[0…n-1]. БЛОК-СХЕМА
Цель лабораторной работы.
С помощью программы установить: - если длина трубы l достаточно большой, то граничные условия практически не влияют на распределение температуры вдоль трубопровода. - если длина трубы l короткая, то θ1 и θ2 влияет на распределение температуры вдоль трубопровода. - изучить влияние α и θ0 на распределение температуры.
Смешанная краевая задача для уравнения параболического типа. Нестационарный теплообмен при перевозке нефти трубопроводом. Постановка задачи
Глубина прокладки нефтепровода Н(м).
Рис. 12 Математическая модель. Ось ОХ направим вертикально вверх (рис. 1). На оси ОХ выделим элемент с координатами х и х + Δх. Тогда приращение энергии в направлений оси х за время Δt будет
С другой стороны, согласно закону сохранения энергий,
Левые части (7.1) и (7.2) равны, поэтому
где ρ – плотность грунта [кг/м3]; с – массовая теплоемкость грунта [кдж/кг.град]; λ – коэффициент теплопроводности грунта [вт/м·град.]. При х = 0 задается температура В основу изучения конвективного теплообмена положен закон Ньютона-Рихмана
где q – плотность теплового потока, вт/м2; θ0 – температура воздуха, 0С; θгр – температура поверхности грунта, 0С; α – коэффициент теплоотдачи, вт/(м2·град); Согласно закону сохранения энергии, количество теплоты, отдаваемый единицей поверхности тела окружающей среде за единицу времени вследствие теплоотдачи, должно быть равно теплоте, которая путем теплопроводности подводится к единице поверхности в единицу времени со стороны внутренних частей тела, т.е.
Равенство (7.3) является математической формулировкой граничного условия третьего рода; оно является действительной для каждого момента времени t.
Получена задача: найти решение нестационарного параболического уравнения со смешанными граничными условиями, т.е.
θ(t,0) = θ1 = const (7.5)
Теорема 1. При определенных условиях на ρ(θ), с(θ) и λ(θ) задача (7.4) - (7.7) имеет единственное решение. Выводы: 5.3. Приближенный метод решения задачи (7.4) – (7.6) Решение задачи (7.4) – (7.6) зависит от двух переменных Q= (0, Тmax)·(0,H), Сетка. Отрезок [0, H] разбиваем на N равных частей с шагом h = H/N, а отрезок [0, Tmax] на М равных частей с шагом ∆t = Tmax /M. Тогда получается сетка (рис. 2).
т.е. функций ρ(θ) и с(θ) определяются на нижних слоях. В начальный момент времени, т.е. при
Вместо задачи (7.4) – (7.7) решается приближенная задача
В системе (7.8) i = 1, 2, …, N-1 при каждом j=0,1,…,M-1.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.48.72 (0.007 с.) |

 разбиваем на n равных частей с шагом
разбиваем на n равных частей с шагом  . Тогда получится сетка
. Тогда получится сетка  .
.




 - правая разностная производная,
- правая разностная производная,  - левая разностная производная.
- левая разностная производная.

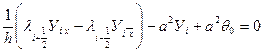 (4.3)
(4.3) ,
,  . (4.4)
. (4.4) .
.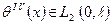 , то решение разностной задачи (4.3) – (4.4) сходится к решению (4.1) – (4.2) при
, то решение разностной задачи (4.3) – (4.4) сходится к решению (4.1) – (4.2) при  и справедливо неравенство
и справедливо неравенство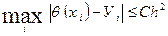 (4.5)
(4.5) можно взять решение приближенной задачи (4.3) – (4.4).
можно взять решение приближенной задачи (4.3) – (4.4).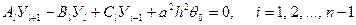 (4.6)
(4.6)
 .
. неизвестными. Данная система имеет единственное решение.
неизвестными. Данная система имеет единственное решение. (4.7)
(4.7)
 (4.8)
(4.8) (4.9)
(4.9) .
. . (4.10)
. (4.10) i = n-2, n -3, …, 0.
i = n-2, n -3, …, 0. .
. и
и  , то метод прогонки является устойчивой. То есть, при реализаций схемы ошибки округления не накапливаются.
, то метод прогонки является устойчивой. То есть, при реализаций схемы ошибки округления не накапливаются.







 l=n-1, 0,-1
l=n-1, 0,-1






 l=0, n- 1, 1
l=0, n- 1, 1

 Подогретый до температуры θ1 (град.) нефть перевозится по подземному трубопроводу.
Подогретый до температуры θ1 (град.) нефть перевозится по подземному трубопроводу. Считая,
Считая, 


 что теплоотдача происходит только по вертикальному направлению определить распределение температуры от трубы до поверхности земли.
что теплоотдача происходит только по вертикальному направлению определить распределение температуры от трубы до поверхности земли.
 (7.1)
(7.1) (7.2)
(7.2)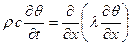
 . На поверхности земли происходит конвективный теплообмен между поверхностью тела и окружающей средой (воздух).
. На поверхности земли происходит конвективный теплообмен между поверхностью тела и окружающей средой (воздух).
 (7.3)
(7.3) называется граничным условием первого рода.
называется граничным условием первого рода.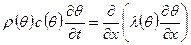 (7.4)
(7.4) (7.6)
(7.6) (7.7)
(7.7) , где t – время, час; х – координата точки грунта, м. Поэтому задача (7.4) – (7.6) решается в области
, где t – время, час; х – координата точки грунта, м. Поэтому задача (7.4) – (7.6) решается в области








 Аппроксимация выражений
Аппроксимация выражений
 .
. (7.8)
(7.8) (7.9)
(7.9) (7.10)
(7.10)


