
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Систему линейных алгебраических уравнений перепишем в видеСодержание книги
Поиск на нашем сайте
i = 1, 2, …, N-1 при каждом j=0,1,…,M-1. где
Метод прогонки для решения разностной схемы. Система (7.9) – (7.10) является системой линейных алгебраических уравнений с N-1 неизвестными. Полученная задача решается методом прогонки. Пусть
После подстановки в (7.11) получится рекуррентная формула
Для определения
где
Сравнивая (7.14) с (7.12) получаем, что
Теперь из (7.12), (7.15) определяются все
После этого рассматривая совместно (7.12) и (7.9) вычисляются все
В данном случае все условия теоремы 2 из §4 выполняются, поэтому метод прогонки для решения задачи (7.9) – (7.11) является устойчивой.
Расчетная схема
1) Используя заданные функций
2) Из рекуррентного соотношения
определяются все 3) После этого используя формулу правой прогонки
определяются все
Переменные и блок – схема
В данном случае искомая функция БЛОК-СХЕМА
описание термодинамических характеристик грунта. - - - - -
Вычисление параметров разностной схемы и начальной функций
  
коэффициента прогонки
рис. 3.
Если M и N достаточно большие величины, то в оперативной памяти компьютера может не хватит места для массива Теорема 3. Пусть решение дифференциальной задачи (7.4)-(7.7) θ обладает непрерывными производными до четвертого порядкаи если Алгоритм реализации схемы расчета приведен на рис. 3. Задания для лабораторной работы. Составить программу и произвести расчет при следующих начальных данных распределения температуры и теплопроводных характеристиках грунта. 1) Температура воздуха изменяется по закону
Варианты значений θmax и θmin:
Глубина заложения трубопровода Н = 1,5 м; tmax =24 час, считаем, что начальное распределение температуры от трубопровода до поверхности изменяется по закону
Температура на поверхности трубопровода равен θ1 = 450.
Теплопроводные характеристики грунта приведены в таблице 1.
Обратная задача для уравнения теплопроводности Постановка задачи
Пусть
Тогда процесс распространения тепла на отрезке
В прямой задаче надо найти Для единственности решения прямой задачи необходимо задать начальные условия
и по одному условию на каждой из границ, например, поток
Если данные прямой задачи (1)-(4) достаточно гладкие и
Обратная задача Пусть о решении прямой задачи (1)-(4) известна дополнительная информация
Требуется определить один из коэффициентов уравнения (1) (или какую-либо их комбинацию) из соотношений (1)-(5). Численное решение обратной задачи (1)-(5) будем искать при
Зададим начальное приближение Приближение
Здесь
Обратная задача 1: найти коэффициент
Найдем приращение функционала (6):
Здесь
Рассмотрим сопряженную задачу:
Умножим обе части равенства (12) на функцию
Проинтегрируем по частям выражение
Имеем
Тогда учитывая условия (13)-(15) и (17)-(19), получим, что
Последние два слагаемых в правой части равенства (21) имеют второй порядок малости. Тогда получаем следующий градиент функционала
Здесь
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 227; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.10.75 (0.006 с.) |

 (7.11)
(7.11)
 . (7.12)
. (7.12) (7.13)
(7.13) преобразуя (7.10) приводим его к виду
преобразуя (7.10) приводим его к виду (7.14)
(7.14)
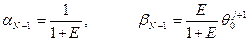 (7.15)
(7.15)


 вычисляются
вычисляются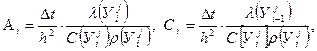 (7.16)
(7.16)


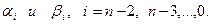

 .
. зависит от двух переменных t и х. Поэтому соответствующая сеточная функция
зависит от двух переменных t и х. Поэтому соответствующая сеточная функция  зависит от двух дискретных переменных i и j. При программировании мы должны резервировать место в оперативной памяти компьютера для двухмерного массива.
зависит от двух дискретных переменных i и j. При программировании мы должны резервировать место в оперативной памяти компьютера для двухмерного массива.






 J = 0, M - 1, 1
J = 0, M - 1, 1






 I = N-1, 1, -1
I = N-1, 1, -1




 I = 0, N - 2, 1
I = 0, N - 2, 1



 .
.  отводятся одномерные массивы
отводятся одномерные массивы  . В формуле (7.16) при определений Ai,Ci,B i используется отношение
. В формуле (7.16) при определений Ai,Ci,B i используется отношение  . Если это выражение очень большое, то вычислительный процесс будет не устойчивой. В этом случае не выполняется теорема 2.
. Если это выражение очень большое, то вычислительный процесс будет не устойчивой. В этом случае не выполняется теорема 2. , то решение разностной схемы (7.8) – (7.10) сходится к решению дифференциальной задачи (7.4) – (7.7).
, то решение разностной схемы (7.8) – (7.10) сходится к решению дифференциальной задачи (7.4) – (7.7). .
.
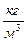

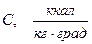
 - коэффициент теплопроводности,
- коэффициент теплопроводности, - температура в точке z в момент времени t.
- температура в точке z в момент времени t. описывается уравнением
описывается уравнением
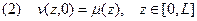

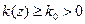 , то решение прямой задачи существует и единственно.
, то решение прямой задачи существует и единственно.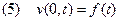
 , минимизируя целевой функционал
, минимизируя целевой функционал
 .
. будем вычислять методом простой итерации
будем вычислять методом простой итерации
 - достаточно малое число,
- достаточно малое число,  - градиент функционала
- градиент функционала  .
. из соотношений:
из соотношений:

 .
.  является решением следующей задачи
является решением следующей задачи

 и проинтегрируем по области
и проинтегрируем по области 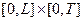 :
:







