
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несобственный интеграл с бесконечными пределамиСодержание книги
Поиск на нашем сайте
Для того, чтобы приближенно вычислить сходящийся несобственный интеграл
с точностью до ε, представляют его в виде
где
Затем определенный интеграл
вычисляют по одной из квадратурных формул с точностью ε/2 и приближенно полагают
В практических расчетах найти величину
и проверяется неравенство
и так далее. Задача 5. Расчет технологических показателей слоисто-неоднородного пласта. Нефтяное месторождение разрабатывается с применением заводнения по однородной схеме расположения скважин. Элемент однорядной схемы расположения скважин, содержащий 0,5 добывающий и 0,5 нагнетательной скважины (всего одну скважину), показан на рис. 45, откуда видно, что расстояние между линией нагнетания и линией отбора l =500м, а расстояние между скважинами (ширина элемента)
Рис. 8
слоистого пласта [16], состоящего из тонких гидродинамических изолированных пропластков, абсолютная проницаемость которых, подчиняется логарифмически нормальному закону с плотностью распределения по формуле
При этом средняя проницаемость пласта
Рис. 9
Будем считать, что вытеснение нефти водой из отдельных пропластков происходит в соответствии с вытеснением по модели поршневого вытеснения (рис.9), причем во всех пропластках остаточная нефтенасыщенность постоянная, равная Sпост = 0,45. В соответствии с моделью поршневого вытеснения нефти водой относительные проницаемости нефти впереди фронта вытеснения kн и для воды позади фронта вытеснения kв постоянны и одинаковы для всех пропластков, так что kн = 1, kв = 0,5. Разработка осуществляется при постоянном перепаде между линиями нагнетания и отбора, равном Решение. Для того, чтобы получить формулы для расчета дебитов нефти и воды с учетом вероятностно-статистического распределения пропластков по проницаемости, сложим все пропластки в один «штабель», в нижней части которого расположен пропласток с «бесконечно большой», а вверху – с нулевой проницаемостью. Поскольку принимается, что абсолютная проницаемость некоторого пропластка в слоистом пласте может быть «бесконечно большой», обводнение такого слоистого пласта начнется в момент закачки воды, т.е. в момент времени t = 0. Другие пропластки, имеющие конечную проницаемость, будет обводняться в соответствующие моменты времени. Время t обводнения пропластка, имеющего проницаемость определяется по формуле [4]:
Расход воды, закачиваемой в обводнившую часть слоистого пласта, равна
Нефть добывается из необводнившихся, пропластков с проницаемостью
Дебит жидкости
Чтобы определить изменение во времени текущей нефтеотдачи элемента hэ=hэ(t), можно определить накопленную добычу нефти элемента по формуле
и затем разделить ее на геологические запасы нефти в элементе. Так как добыча нефти исчисляется в объемных единицах, приведенных к пластовым условиям, будем определять не геологические запасы нефти элемента в массовых единицах, а объем нефти Vнэ в пластовых условиях в элементе пласта. Имеем
Текущая нефтеотдача составит hэ = θнэ/Vнэ. Определение показателей разработки месторождения. Согласно плану разбуривания и обустройства месторождения ежегодно в течение шести лет, т.е. в течение срока ввода месторождения в разработку, в эксплуатацию передается по 50 элементам. Всего за 15 лет будет введено в эксплуатацию 300 элементов. Для простоты считаем, что добыча нефти с разбуриваемых и обустраиваемых элементов будет происходить с начала каждого года. Для определения добычи нефти и воды в целом по месторождению суммируются добыча нефти воды по элементам. Обводненность добываемой из месторождения продукции вычисляют по формуле
всего по месторождению в разработку вовлекается объем нефти в пластовых условиях
Коэффициент охвата по месторождению в целом
Нефтеотдача по месторождению в целом определяется как отношение объема накопленной добычи нефти
к первоначальному объему нефти в пласте Vн. Задача 6. При разработке нефтяного месторождения, имеющего площадь нефтеопасности S = 2494,08×104 м2, использована площадное заводнение при семиточечной схеме расположения скважин. Расстояние между двумя добывающими или между добывающей и нагнетательной скважинами Скорость ввода элементов в разработку – 10 элементов за год, срок ввода месторождения в разработку – 6 лет. Таким образом, всего в разработку вводится 60 элементов. Требуется определить изменение в течение 15 лет следующих показателей: 1. Добычи нефти, обводненности продукции и текущей нефтеотдачи для одного элемента разработки. 2. Добычи нефти, воды и текущей нефтеотдачи для месторождения в целом. Решение. Проницаемость k* пропластков, обводнившихся к моменту времени t определяется по формуле:
Будем приближенно считать, что при разработке элемента семиточечной системы происходит радиальное вытеснение нефти водой, закачиваемой в нагнетательную скважину, к «контуру отбора», имеющему форму окружности радиуса R (рис.10), на которой находится добывающие скважины. Элементарный расход воды dqi, поступающей в i -й пропласток толщиной dhi, в этом случае составит
Рис. 10
Будем предполагать, что в некоторый момент времени t фронт воды, вытесняющий нефть из i- го пропластка, продвинулся на расстояние rв от начала координат (рис. 10). Разделяя переменные в приведенном выражении и интегрируя в пределах rc £ r £ rв, получаем
где
где Рк – давление на контуре добывающих скважин. Из последних двух равенств следует, что
где Рс – давление на нагнетательной скважине, Рк – давление на добывающей скважине. Для того, чтобы получить формулы для расчета дебитов нефти и воды с учетом вероятностно-статистического распределения пропластков по проницаемости, сложим все пропластки в один «штабель» в нижней части которого расположен пропласток с «бесконечно большой», а вверху – с нулевой проницаемостью. Тогда общая толщина h слоев с проницаемостью не ниже k0, отсчитываемая от кровли штабеля пропластков-модели слоистого пласта, будет выражаться по формуле соответствующего вероятностно-статистического закона распределения проницаемости
где Н – общая толщина слоистого пласта. Дифференцируя, равенство имеем
где f(k) – вероятностно-статистическая плотность. То есть dh = Hf(k)dk. Учитывая это, на основе формулы (30) получим следующие выражения для дебита нефти, приведенного к пластовым условиям и воды:
Выражение для элементарного расхода воды, поступающей в i -й пропласток можно написать, рассматривая согласно рис.47 характер перемещения со временем фронта вытеснения нефти водой i -м пропластке и распределения в нем остаточной нефтенасыщенности пласта связанной водой имеем
Приравнивая правые части (30) и (31) и опуская индекс i, получаем
Выполняя интегрирование при ∆Рс = const, приходим к следующему соотношению определения rв при различных значениях времени t.
Поскольку принимается, что абсолютная проницаемость некоторого пропласта в слоистом пласте может быть «бесконечно большой», обводнение такого слоистого пласта начнется в момент закачки воды, т.е. в момент времени t = 0. Другие пропластки, имеющие конечную проницаемость, будет обводняться в соответствующие моменты времени. Поэтому, чтобы найти проницаемость Замечание. Для прямолинейного вытеснения нефти водой уравнение (31) принимает вид:
где в – ширина элемента, хв(t) – продвижение воды за время t.
Замечание. Абсолютная проницаемость гидродинамический изолированных слоистых пропластков могут подчиняться гамме-распределения, плотность которого определяется по формуле
Задания для лабораторной работы.
Задача 7. Предположим, что плоский пласт состоит из двух областей с различными свойствами (проницаемостью, пористостью и т.д.), разделенных прямолинейной границей (рис. 11). Пусть в момент t = 0 первоначально стационарное состояние возмущается в результате пуска скважины в точке (а, 0) с постоянным расходом q. Тогда распределенные давления в каждой из областей описывается уравнениями.
На границе х = 0 выполняются условия непрерывности давлений и потоков:
Рис. 11
Во втором уравнений (33) в правую часть непосредственно введен точечный источник интенсивности q. Через δ, как обычно, обозначена дельта-функция, определяемая условиями
Решение. В работе [5] при
Пусть теперь имеется обратная неравенство:
Замечание. П.Я. Полубаринова-Кочина рассмотрела аналогичную стационарную задачу и показала, что распределение давления в той части пласта, где находится источник, совпадает с распределением давления в однородной среде при действий двух источников интенсивностью Задания для лабораторных работ.
2. Интерполирование функций. Сплайны первого и второго порядка.
Постановка задачи. Функция у = f(x) задана в табличном виде
в точках Найти приближенное значение функции у = f(x) в промежуточных точках
Решение. Если аналитический вид функции у = f(x) неизвестен, то значения функции
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.152 (0.009 с.) |


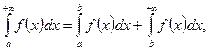
 выбирают настолько большим, чтобы имело место неравенство
выбирают настолько большим, чтобы имело место неравенство
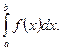


 если да, то в качестве значении исходного интеграла берется
если да, то в качестве значении исходного интеграла берется  , если нет, то вычисляется интеграл
, если нет, то вычисляется интеграл  и проверяется неравенство
и проверяется неравенство

 м. Продуктовый пласт неоднородный. Его можно представить модельно
м. Продуктовый пласт неоднородный. Его можно представить модельно

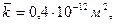 общая толщина пласта h0 = 18,75м, охваченная заводнением толщина пласта h = 15м (коэффициент охвата 0,8). Принимается, что пористость всех пропластков слоистого пласта m = 0,2, начальная насыщенность связанной водой Sсв = 0,1. Вязкость нефти в пластовых условиях μн = 2мПа×С, вязкость воды μв = 1мПа×С.
общая толщина пласта h0 = 18,75м, охваченная заводнением толщина пласта h = 15м (коэффициент охвата 0,8). Принимается, что пористость всех пропластков слоистого пласта m = 0,2, начальная насыщенность связанной водой Sсв = 0,1. Вязкость нефти в пластовых условиях μн = 2мПа×С, вязкость воды μв = 1мПа×С.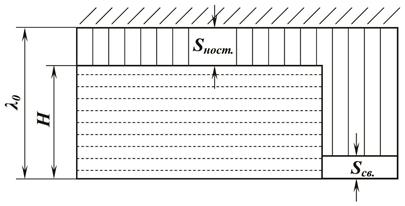
 Предполагается, что за весь рассматриваемый период ни один элемент системы не выбивает из разработки. Требуется рассчитать изменение в течение 15 лет следующих показателей разработки месторождения: добыча нефти, обводненность продукции и текущей нефтеотдачи.
Предполагается, что за весь рассматриваемый период ни один элемент системы не выбивает из разработки. Требуется рассчитать изменение в течение 15 лет следующих показателей разработки месторождения: добыча нефти, обводненность продукции и текущей нефтеотдачи.
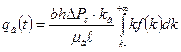
 . Формула для дебита нефти из слоистого пласта имеет вид
. Формула для дебита нефти из слоистого пласта имеет вид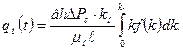
 Обводненность добываемый из слоистого пласта имеет продукции
Обводненность добываемый из слоистого пласта имеет продукции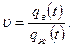


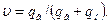

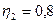 . Поэтому общий объем нефти в пласте
. Поэтому общий объем нефти в пласте

 . Радиус нагнетательной скважины rc = 0,1м. Продуктивный пласт неоднородный по толщине и его можно представить моделью слоисто-неоднородного пласта. Плотность распределения абсолютной проницаемости соответствует логарифмическому закону. При этом k = 0,25×10-12 м2, σ = 0,5. Общая толщина пласта составляет 25м, а толщина пропластков, вовлекаемых в разработку, h = 20м. Пористость нефтенасыщенных пород m = 0,23, вязкость нефти в пластовых условиях μн = 2,5мПа×С, вязкость воды μв = 1мПа×С. Насыщенность пласта связанной водой Sсв = 0,1. Вытеснение нефти водой происходит поршневым способом, при этом для всех пропластков kн =1, kв =0,4, Sност =0,4, так что μв/ kв = μн/ kн. Перепад давления между нагнетательной скважиной и контуром отбора радиусом R составляет ∆ρс = 2×106Па.
. Радиус нагнетательной скважины rc = 0,1м. Продуктивный пласт неоднородный по толщине и его можно представить моделью слоисто-неоднородного пласта. Плотность распределения абсолютной проницаемости соответствует логарифмическому закону. При этом k = 0,25×10-12 м2, σ = 0,5. Общая толщина пласта составляет 25м, а толщина пропластков, вовлекаемых в разработку, h = 20м. Пористость нефтенасыщенных пород m = 0,23, вязкость нефти в пластовых условиях μн = 2,5мПа×С, вязкость воды μв = 1мПа×С. Насыщенность пласта связанной водой Sсв = 0,1. Вытеснение нефти водой происходит поршневым способом, при этом для всех пропластков kн =1, kв =0,4, Sност =0,4, так что μв/ kв = μн/ kн. Перепад давления между нагнетательной скважиной и контуром отбора радиусом R составляет ∆ρс = 2×106Па. (32)
(32)
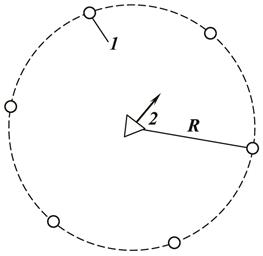

 – давление на фронте вытеснения нефти водой. Впереди фронта вытеснения движется нефть. Поэтому после интегрирования аналогичного выражения для нефти в пределах rв £ r £ R имеем
– давление на фронте вытеснения нефти водой. Впереди фронта вытеснения движется нефть. Поэтому после интегрирования аналогичного выражения для нефти в пределах rв £ r £ R имеем
 (30)
(30)


 (31)
(31)

 пропластков, обводнившихся к моменту времени t = t*, необходимо положить в последнем равенстве rв=R. Тогда получим формулу (32).
пропластков, обводнившихся к моменту времени t = t*, необходимо положить в последнем равенстве rв=R. Тогда получим формулу (32).

 , a
, a
 (33)
(33)


 (малые времена) получено
(малые времена) получено
 , в этом случае распределение давления имеет вид:
, в этом случае распределение давления имеет вид:
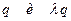 (где
(где  ) расположенных симметрично относительно границы раздела.
) расположенных симметрично относительно границы раздела. ,
, 

 вычисляются приближенно. Приближенные методы вычисления
вычисляются приближенно. Приближенные методы вычисления 


