
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра информационные системы и математическое моделированиеСодержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
КАФЕДРА ИНФОРМАЦИОННЫЕ СИСТЕМЫ И МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Рысбайулы Б.
О П О Р Н Ы Й К О Н С П Е К Т Л Е К Ц И Й По дисциплине Численные методы . (Для студентов специальности "математическое и компьютерное моделирование")
АЛМАТЫ 2014 1. Приближенное вычисление определенного интеграла
В настоящем пункте рассматриваются способы приближенного вычисления определенных интегралов
Введем на [а, в] равномерную сетку с шагом h, т.е. множества точек
и представим интеграл в виде суммы интегралов по частным отрезкам:
Для построения формулы численного интегрирования на всем отрезке [а, в] достаточно построить квадратичную формулу для
Формула прямоугольников Заменим интеграл Si выражением
Рис. 1
Тогда получим формулу
которая называется формулой прямоугольников на частичном отрезке [хi-1, хi]. Погрешность метода (26) определяется величиной
которую легко оценить с помощью формулы Тейлора. Действительно, запишем ψi в виде
и воспользуемся разложением
Обозначая
Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива формула
т.е. формула имеет погрешность О(h3) при h→0. Суммируя равенства (26) по I от 1 до N, получим составную формулу прямоугольников
Погрешность этой формулы
Отсюда, обозначая
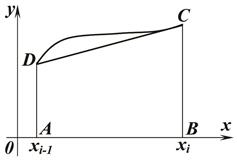
т.е. погрешность формулы прямоугольников на всем отрезке есть величина О(h2). В этом случае говорят, что квадратурная формула имеет второй порядок точности. Определение. Приближенное равенство
Называется квадратурной формулой.
Формула трапеции
На частичном отрезке (хi-1, xi) площадь криволинейной трапеции АВСД заменяется площадью прямоугольной трапеции АВСД (рис. 2).
Рис. 2
Тогда
Для оценки погрешности
Представим его в виде
Отсюда получим
Составная формула трапеции имеет вид
Погрешность этой формулы оценивается следующим образом:
Таким образом, формула трапеции имеет вид, так же как и формула прямоугольников, второй порядок точности, Применение формулы трапеции или прямоугольников требует оценки второй производной
Отсюда видно, что формула прямоугольников и трапеции дает достаточную точность только при достаточно малых разностях второго порядка ∆2Уk (а именно, когда произведения Для уточнения величины интеграла можно использовать, то обстоятельство, что с уменьшением шага h в два раза погрешность формулы трапеций уменьшается примерно в четыре раза. Отсюда следует, что совпадающие знаки в значениях интеграла, вычисленных с шагом h и
Формула Симпсона
При аппроксимации интеграла
Тогда
Вычислим
Из (27) получим, что
Таким образом, приходим к приближенному равенству
которое называется формулой Симпсона.
Погрешность этой формулы ψi оценивается так [1]:
На всем отрезке [a, в] формула Симпсона имеет вид
Погрешность этой формулы оценивается неравенством:
Из этой оценки видно, что с уменьшением шага h в два раза погрешность формулы Симпсона уменьшается примерно в 16 раз; поэтому значение интеграла, вычисленное с шагом 1.4. Задача 1 Между двумя параллельными сбросами
Рис. 3
Отбор жидкости из залежи изменяется во времени следующим образом
где
Решение. В начале определим пьезопроводность пласта по формуле
Для расчета изменения во времени давления на контуре нефтяной залежи используя аппроксимацию Карслоу и Егеря [2] имеем:
Данный интеграл вычисления одним из методов: метод прямоугольников, трапеции или Симпсона. Решение задачи 2
Рис. 5
Для расчета изменения во времени давления на контуре нефтяной залежи, используя аппроксимацию соответствующих решений Карслоу и Егера, имеем
Этой формулой можно пользоваться, если приток воды из законтурной области пласта к нефтяной залежи цилиндрической формы с постоянным дебитом. Однако, по условиям данной задачи в период разбурения месторождения объем воды, поступающей из законтурной области, и следовательно, отбираемой жидкости из пласта – переменные во времени. Поэтому для расчета давления на контуре нефтяного месторождения Pкон (t) необходимо использовать интеграл Дюамеля, согласно которому
В условиях задачи qж зависит от физического времени t. В интеграл необходимо поставить
Это формула применяется в том случае, если
Задание для лабораторной работы.
Структурная схема расчета.
- - - - - - - - - - ввод начальных данных
Рис.6 Фильтрация жидкости и газа Теория фильтрации изучает движение газов, жидкостей и их смесей в порах, т.е. в твердых телах, пронизанных системой сообщающих между собой пустот (пор), что делает их проницаемой для жидкостей. Пористая среда состоит огромного числа случайно расположенных зерен различной формы и величины. Поэтому пространство, в котором движется жидкость, представляет собой систему пор, непрерывно переходящих одна в другую. Для пористой среды характерно свойство сообщаемости пор. Из-за нерегулярности строения порового пространства его нельзя полностью описать никаким конечным набором параметров; для целей теории фильтрации, однако, достаточно небольшого числа осредненных характеристик. Важнейшая характеристика пористой среды – ее пористость Самым простым и наиболее изученным случаем нестационарной фильтрации является фильтрация слабосжимаемой жидкости в упругодеформируемом пласте (в технических приложениях эти задачи получили название задач упругого режима фильтрации). В основу исследования кладется система уравнений закона фильтраций и уравнения неразрывности:
Здесь
Здесь Рассмотрим постановку основных задач теории упругого режима. Определим распределение давления
и задать начальное распределение давления в области Д
то существует распределение давления
Рассмотрим подробнее физический смысл тех или иных дополнительных условий. Область, в которой ищется распределения давления жидкости, обычно представляет собой пористый пласт, частично имеющий непроницаемые границы, а частично сообщающийся с другими пластами и вскрывающими его скважинами. На непроницаемых границах должно удовлетворяться очевидное условие отсутствие потока – равенство нормального компонента скорости фильтрации нулю:
Un = 0,
Откуда используя закон Дарси, получаем.
На участках границы с областями, в которых перераспределение давления практически не происходит (область питания), давление можно считать постоянным, так что
Такое условие справедливо, если, например, рассматриваемый пласт граничит с высокопроницаемой областью, запас жидкости, в которой весьма велик. Давление на границе такой области близко к среднему давлению в ней и ввиду ее большего объема мало зависит от процессов, происходящих в исследуемой области. Характерным примером является нефтяная залежь, окруженная со всех сторон обширной водоносной областью. При рассмотрении нестационарных процессов в залежи давление в водоносной области можно считать постоянным. Следует, однако, отчетливо представлять себе, что понятие области постоянного давления не является абсолютным. Чем более длительный характер носят изменения давления, тем на большую область они распространяются. Часть границы области фильтрации обычно образована стенками скважины и дренажных галерей. На этой части границы чаще всего задается либо давление жидкости, либо поток ее через стенки скважины. Выбор того или иного условия зависит от режима работы скважины или галерей. Могут быть и более сложные условия, когда задается связь давления с расходом жидкости. Задание потока жидкости согласно закону Дарси эквивалентна заданию нормальной производной от давления. Условия этого типа выполняются на тех участках границы, через которые может происходить обмен жидкости с соседними пластами через сравнительно слабопроницаемые перемычки. Если толщина перемычки Δ мала, а давление
uде Un – нормальная проекция скорости фильтрации на рассматриваемом участке границы. Отсюда имеем
т.е. условия третьего рода. Все три типа условий являются частными случаями общего условия. Таким образом, задавая начальные распределения давления и указанные условия на границе, получаем однозначно разрешимую задачу. Задача 3. Одинарное прямолинейно-параллельное движение. Пусть скорость фильтрации жидкости параллельны оси х и не зависит от координат y и z. Давление при этом удовлетворяет уравнению
При х = 0 задан расход жидкости q(t). При заданных значениях μ, k, x и L определить давление пласта.
Решение. В работе [5], предполагая, что
Полученная формула имеет двоякий смысл. С одной стороны, он описывает распределение давления в пласте конечной длины L при малом времени. С другой стороны он дает распределение давления в произвольный момент времени. В пласте «бесконечной» протяженностью L → ∞. Дело в том, что конечное (не бесконечно малое) изменения давления распространяется за заданное время лишь на конечное расстояние и, если рассматриваются малые времена, можно считать пласт бесконечным. Решение задачи для бесконечного пласта автомодельное: независимые переменные х и t входят в решение не порознь, а лишь в комбинации Если
Первый член этого выражения представляет собой стационарное решение, отвечающее заданным краевым условиям
P 1 (0, t) = P0, P(L, t) = P(L, 0) = const;
второй член выражает основную, при больших временах, часть поправки к этому стационарному решению. Таким образом, приближение к стационарному режиму происходит экспоненционально, причем характерное время выхода на стационарный режим порядка
Оценим это время для систем различных режимов. При этом для χ характерное значение х = 104см2/сек. В результате имеем: при L = 1м (переходный процесс в одном пуске-блике породы) t = 0,1сек; при L = 300м (порядка расстояния между скважинами) t = 104сек»3г. L = 1км (порядка размеров месторождения) t = 107сек £ 100 суткам; L = 100км (порядка размеров крупной водонапорной системы) t = 109сек = 30 лет. В практических расчетах часто приходится рассматривать нестационарные процессы в сложных системах, в которые входят элементы с различными собственными временами. Оценивая время установки (стационарного течения) для каждого элемента по его размерам мы упростим задачу, отделив те элементы, движение в которых уже можно считать стационарными, а те, в которых нестационарный процесс находится в начальной стадии. Задания для лабораторной работы.
Задача 4. Рассмотрим теперь одномерное осесимметричное (плоско-радиальное) движение при упругом режиме. Распределение давления определяется при этом как решение уравнения теплопроводности в полярных координатах (r, j):
удовлетворяющие начальному условию
P (r, 0) = f(r)
а граничным условиям при r = ρ и r = R. По прежнему основной интерес представляют решения, отвечающие стационарному начальному распределению давления
f(r)=C1lnr+C2.
В приложениях особое значение имеет задача, в которой на скважине задается не постоянное давление, а постоянный дебит. Решение этой задачи используется в наиболее распространенных способах определения параметров пласта по наблюдениям нестационарного притока к скважине. Положим таким образом
где
Рис. 7
Предполагая, что
Отметим важное обстоятельство: в соотношения для P (r, t) не входит радиус скважины (28) – является несобственным интегралом, с помощью замены переменной приведем его собственному интегралу. Для этого сделаем замену:
Первоначальное дифференциальное уравнение является линейным, поэтому здесь применим принцип суперпозиции. Если имеется две скважины расположенные друг от друга на расстоянии l, то давление пласта в точке А удаленной от первой скважины на расстоянии будет равен (рис. 7)
Задания для лабораторной работы
Сплайн 2-го порядка S(x) На каждом из отрезков (xi, xi +1) функция у = f(x) приближается параболой
S(x) = В узлах х = хi ставятся следующие условия
1)
2)
xi , i = 1, 2, …, n-1. 3) S (x) в узлах xi , i = 1, 2, …, n-1.
Используя 1) - 3) определяем аi, bi, сi.
1. Из условия
Сюда можно дописать дополнительный коэффициент 2. Из условия 2) и 3) получаем систему Постановка задачи Задача. Длинный трубопровод с теплопроводностью λ (ккал/м.час град.) находится в состоянии теплового равновесия, т.е. температура точек трубопровода не изменяется во времени. Потеря тепла через поверхность трубопровода в окружающую среду, температура которой
Математическая модель
Строго говоря, решение этой задачи приводит к дифференциальному уравнению с частными производными, так как температура в поперечном сечений трубопровода не вполне постоянна и является функцией расстояния х и расстояния поверхности стержня. Однако, если трубопровод достаточно тонкий и если теплопроводность его велика, то мы можем без существенной ошибки пренебречь температурными градиентами в направлениях перпендикулярных к оси трубопровода и принять температуру постоянной в каждой точке поперечного сечения, перпендикулярного оси Ох. При таком допущении температура является функцией только одного независимого переменного х и распределение температуры может быть описано обыкновенным дифференциальным уравнением. Пусть длина стержня равна l м, периметр поперечного сечения p м, площадь поперечного сечения Q м2. Исследуем процесс распространения тепла в элементарном отрезке длиной dx на расстоянии х от того конца стержня, температура которого t1. Количество тепла проходящего за время dt через сечение трубопровода находящееся на расстоянии х от начало трубопровода, согласно теории теплопередачи, будет равно:
Количество тепла, прошедшее за время dt через сечение, находящееся на расстоянии х + dx от начала, будет равна:
Участок стержня, заключенный между сечениями, отстоящими от начала на расстояниях х и х + dx, вследствие теплопроводности, приобретает за время dt количество тепла, равное разности указанных количеств, т.е.:
За то же время потеря тепла от этого же участка в окружающую среду будет равна:
Но так как изучаемый нами процесс является стационарным, то:
Окончательно мы приходим к следующему дифференциальному уравнению:
В итоге получена задача:
Это уравнение с постоянными коэффициентами. Его общий интеграл будет:
Используя граничные условия, составим систему:
откуда
Подставляя значения С1 и С2 получим:
Выделим элемент длины dх, находящийся на расстояний х от левого конца, и примем его температуру равной
а через правую на расстоянии х+dх от конца
Таким образом, выделенный участок приобретает за время
Вместе с тем потеря тепла этого элемента через поверхности в окружающую среду равна
Вследствие предположения о стационарности процесса эти количества равны, т.е.
откуда
Пусть на обоих концах стержня поддерживается постоянная температура
Численный пример. Пусть a = 10 l = 300 ккал/м×час×град
При этом случае получится зависимость
Переменные. Блок-схема
Из определения Аі, Ві, Сі следует равенства
Сі = Аі -1, Ві = Аі +Аі - 1 + а2 h2
Поэтому, (4.9) можно переписать в виде
На основе этих формул, при программировании используются массивы A[0…n], α[0…n-1], β[0…n-1]. БЛОК-СХЕМА
Цель лабораторной работы.
С помощью программы установить: - если длина трубы l достаточно большой, то граничные условия практически не влияют на распределение температуры вдоль трубопровода. - если длина трубы l короткая, то θ1 и θ2 влияет на распределение температуры вдоль трубопровода. - изучить влияние α и θ0 на распределение температуры.
Постановка задачи
Глубина прокладки нефтепровода Н(м).
Рис. 12 Математическая модель. Ось ОХ направ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.62.94 (0.013 с.) |

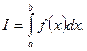
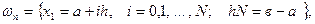
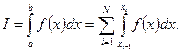
 на частном отрезке [хi-1, хi].
на частном отрезке [хi-1, хi]. Геометрический такая замена означает, что площадь криволинейной трапеции АВСД заменяется площадью прямоугольника АВС1Д1 (см. рис. 1).
Геометрический такая замена означает, что площадь криволинейной трапеции АВСД заменяется площадью прямоугольника АВС1Д1 (см. рис. 1).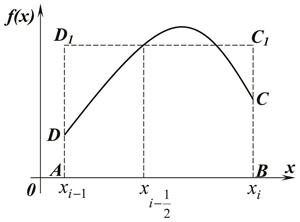
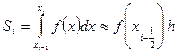 (26)
(26)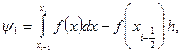


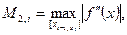 оценим ψi следующим образом:
оценим ψi следующим образом:


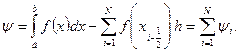
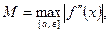 получим
получим 
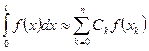 .
.

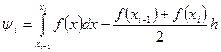

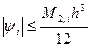
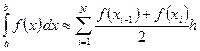
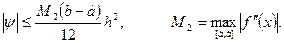
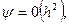 но ее погрешность оценивается величиной в два раза большей.
но ее погрешность оценивается величиной в два раза большей. на отрезке [а, в]. Если такая оценка затруднительна (или вообще невозможно, например, в случае функции определяемых опытным путем), то в предположений малого изменения (или монотонности) второй производной
на отрезке [а, в]. Если такая оценка затруднительна (или вообще невозможно, например, в случае функции определяемых опытным путем), то в предположений малого изменения (или монотонности) второй производной 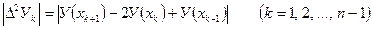
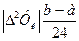 не превосходят допустимой погрешности расчета).
не превосходят допустимой погрешности расчета). можно считать верным. Действительно, если погрешность значения интеграла, вычисленного с шагом
можно считать верным. Действительно, если погрешность значения интеграла, вычисленного с шагом 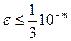 , а это означает, что в значений интеграла вычисленном с шагом
, а это означает, что в значений интеграла вычисленном с шагом 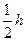 , все m десятичных знаков верны (здесь предполагается, что погрешность исходных данных пренебрежимо мало).
, все m десятичных знаков верны (здесь предполагается, что погрешность исходных данных пренебрежимо мало).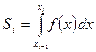 заменяем функцию f(x) параболой, проходящей через точки (xI, f(xI)), I = i-1, i-0,5, i, т.е. представим приближенно f(x) в виде
заменяем функцию f(x) параболой, проходящей через точки (xI, f(xI)), I = i-1, i-0,5, i, т.е. представим приближенно f(x) в виде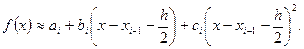
 (27)
(27)
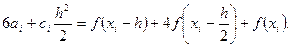


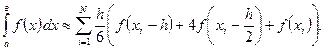
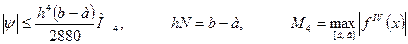
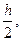 содержащий на один верный знак больше, чем значение интеграла, вычисленное с шагом h. Это правило на практике очень удобно при оценке точности интеграла.
содержащий на один верный знак больше, чем значение интеграла, вычисленное с шагом h. Это правило на практике очень удобно при оценке точности интеграла.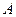 и
и 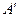 находится нефтяная залежь В (рис.42) за пределами которой расположены бесконечно простирающая водоносная область. Стрелками показан приток воды из законтурной области. Ширина залежи в = 1000м, толщина пласта h =15м, проницаемость водоносной области k = 0,2·10-12м2, вязкость законтурной воды
находится нефтяная залежь В (рис.42) за пределами которой расположены бесконечно простирающая водоносная область. Стрелками показан приток воды из законтурной области. Ширина залежи в = 1000м, толщина пласта h =15м, проницаемость водоносной области k = 0,2·10-12м2, вязкость законтурной воды 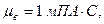 Упругоемкости β как нефтяной, так и водоносной частей одинаковы, причем β = 2,5·10-10 Па-1, вязкость нефти μн = 2мПа·С.
Упругоемкости β как нефтяной, так и водоносной частей одинаковы, причем β = 2,5·10-10 Па-1, вязкость нефти μн = 2мПа·С.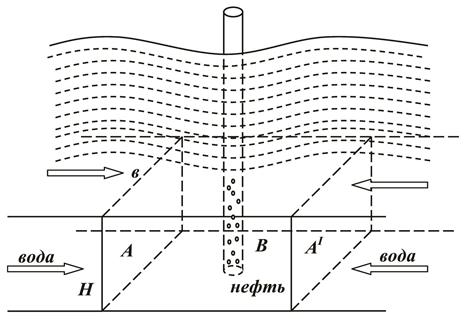
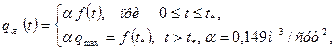
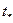 – время ввода месторождения в разработку. Требуется определить изменение давления на контуре нефтеносности
– время ввода месторождения в разработку. Требуется определить изменение давления на контуре нефтеносности  , т.е. по сравнению с начальным давлением после начала разработки залежи.
, т.е. по сравнению с начальным давлением после начала разработки залежи.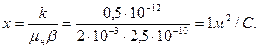




 Поэтому найдем зависимость qж = qж(τ) или, что то же самое, qж = qж(λ). Имеем
Поэтому найдем зависимость qж = qж(τ) или, что то же самое, qж = qж(λ). Имеем

 μ, k, x, H, в, tk, α0,
μ, k, x, H, в, tk, α0,  μ, k, x, H, в, tk, α0,
μ, k, x, H, в, tk, α0,  μ, k, x, H, в, tk, α0,
μ, k, x, H, в, tk, α0,  μ, k, x, H, в, tk, α0,
μ, k, x, H, в, tk, α0,  μ, k, x, H, R, tk, α0, ρ0,
μ, k, x, H, R, tk, α0, ρ0,  μ, k, x, H, R, tk, α0, ρ0,
μ, k, x, H, R, tk, α0, ρ0,  μ, k, x, H, R, tk, α0, ρ0,
μ, k, x, H, R, tk, α0, ρ0,  μ, k, x, H, R, tk, α0, ρ0,
μ, k, x, H, R, tk, α0, ρ0, 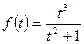

















 t = 0, tmax, Δt ΔP конец
t = 0, tmax, Δt ΔP конец
 , равная отношению объема, занятого в выделенном элементе порами, к общему объему элемента
, равная отношению объема, занятого в выделенном элементе порами, к общему объему элемента  .
.
 -вектор скорости фильтрации;
-вектор скорости фильтрации;  - плотность жидкости. Для того, чтобы получить замкнутую систему уравнений, нужно воспользоваться тем, что свойства жидкости (плотность ρ и вязкость μ), так же как и пористость и проницаемость пористой среды, являются функциями давления (мы предположим движение изотермическим). Исходя, из предположения, слабой сжимаемости жидкости и пористой среды получается уравнение [14-15]:
- плотность жидкости. Для того, чтобы получить замкнутую систему уравнений, нужно воспользоваться тем, что свойства жидкости (плотность ρ и вязкость μ), так же как и пористость и проницаемость пористой среды, являются функциями давления (мы предположим движение изотермическим). Исходя, из предположения, слабой сжимаемости жидкости и пористой среды получается уравнение [14-15]: где коэффициент
где коэффициент  .
. - коэффициент пьезопроводности. Полученное уравнение обычно называется уравнением упругого режима или уравнением пьезопроводности.
- коэффициент пьезопроводности. Полученное уравнение обычно называется уравнением упругого режима или уравнением пьезопроводности. в некоторой замкнутой области пространства D на протяжении промежутка времени 0 ≤ t ≤ T. Из теории уравнения теплопроводности известно, что если задать на границе Г области D линейную комбинацию давления и его производной по нормали к границе области
в некоторой замкнутой области пространства D на протяжении промежутка времени 0 ≤ t ≤ T. Из теории уравнения теплопроводности известно, что если задать на границе Г области D линейную комбинацию давления и его производной по нормали к границе области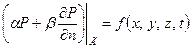
 ,
, , и притом единственное, удовлетворяющее уравнению пьезопроводности, непрерывное в замкнутой области Д, включая границу, и удовлетворяющие начально-граничным условиям. Сформулированная задача охватывает почти все основные задачи теории упругого режима фильтрации.
, и притом единственное, удовлетворяющее уравнению пьезопроводности, непрерывное в замкнутой области Д, включая границу, и удовлетворяющие начально-граничным условиям. Сформулированная задача охватывает почти все основные задачи теории упругого режима фильтрации.
 .
. за ней можно считать постоянным, то расход вытекающей жидкости через участок перемычки площадью ds составит
за ней можно считать постоянным, то расход вытекающей жидкости через участок перемычки площадью ds составит 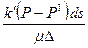 . Это количество жидкости должно быть равно
. Это количество жидкости должно быть равно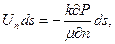

 Предположим, что в плоскости х = L давление сохраняет постоянное значение, равное контурному.
Предположим, что в плоскости х = L давление сохраняет постоянное значение, равное контурному.
 получено решение поставленной задачи. Она описывается в виде:
получено решение поставленной задачи. Она описывается в виде:

 , то [5]
, то [5]

 , t £ T, P0 (x)
μ, k, χ, q(t) = α0ttg
, t £ T, P0 (x)
μ, k, χ, q(t) = α0ttg  ,t £ T, P0 (x)
μ, k, χ, q(t) = α0t2/(t0 + 2) t £ T, P0 (x)
μ, х, q(t) = α0t, t £ T, P (t1), P1 (t1+ Δt)
k, х, q(t) = α0tsin
,t £ T, P0 (x)
μ, k, χ, q(t) = α0t2/(t0 + 2) t £ T, P0 (x)
μ, х, q(t) = α0t, t £ T, P (t1), P1 (t1+ Δt)
k, х, q(t) = α0tsin 


 – постоянная размерность давления.
– постоянная размерность давления.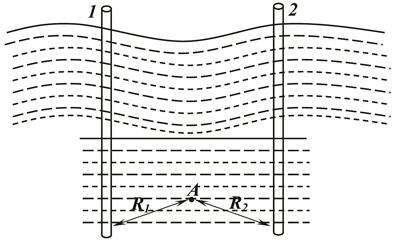
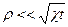 в работе [5] получена решение поставленной задачи в виде
в работе [5] получена решение поставленной задачи в виде (28)
(28) . Это означает, что в области применяемости условия
. Это означает, что в области применяемости условия  распределения не зависит от радиуса скважины.
распределения не зависит от радиуса скважины.



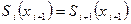 - непрерывность функции S (x) в узлах
- непрерывность функции S (x) в узлах - непрерывность первой производной функции
- непрерывность первой производной функции следует, что
следует, что .
. .
.
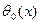 , пропорциональна разности температур с постоянным коэффициентом теплопередачи α (ккал/м2. час град.). Считая температуру θ во всех точах поперечного сечения трубопровода постоянной, найти ее зависимость θ = θ(х) от координаты, отсчитываемой от какого-либо конца.
, пропорциональна разности температур с постоянным коэффициентом теплопередачи α (ккал/м2. час град.). Считая температуру θ во всех точах поперечного сечения трубопровода постоянной, найти ее зависимость θ = θ(х) от координаты, отсчитываемой от какого-либо конца.

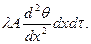


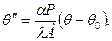





 . За время ∆t через левую границу этого элемента пройдет количество тепла
. За время ∆t через левую границу этого элемента пройдет количество тепла
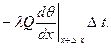
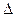 t количество тепла, равное разности
t количество тепла, равное разности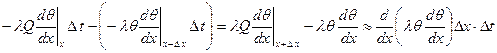 .
.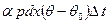 .
.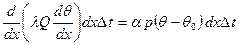
 (4.1)
(4.1) . Тогда краевые условия имеют вид.
. Тогда краевые условия имеют вид. ,
,  (4.2)
(4.2)
 тогда
тогда 

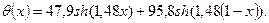








 l=n-1, 0,-1
l=n-1, 0,-1






 l=0, n- 1, 1
l=0, n- 1, 1

 Подогретый до температуры θ1 (град.) нефть перевозится по подземному трубопроводу.
Подогретый до температуры θ1 (град.) нефть перевозится по подземному трубопроводу. Считая,
Считая, 


 что теплоотдача происходит только по вертикальному направлению определить распределение температуры от трубы до поверхности земли.
что теплоотдача происходит только по вертикальному направлению определить распределение температуры от трубы до поверхности земли.



